Friction stir welding (FSW) is a green manufacturing process that does not liberate smoke, fume and odour unlike the conventional arc welding. This research article aims at finding the ultimate tensile strength of the Aluminium matrix composites welded by FSW with the process parameters such as tool rotation speed, weld traverse speed and axial force. The search optimization is carried out in two phases using MATLAB environment. Firstly, the regression equation of the experiments is utilized to find the better design points by Genetic Algorithm (GA) through pool generation, cross-over and mutation. Secondly, the top design points obtained in GA are stored in a new pool, from which the global best optimal design is selected by Firefly Algorithm (FA). Since, every algorithm has different features and highlights, the coupled GA-FA algorithm is utilized to obtain the optimal point that gives the best ultimate tensile strength of the welded composite. The results demonstrate that the optimal points are distributed in several points of design space that needs to be searched out by the effective optimization strategy. The convergence rate, speed of the optimization and coverage of the design points are also improved. The algorithm shows good agreement with the confirmation tests also with errors less than 5%.

Keywords: Optimization, Metaheuristics, Genetic algorithm, Firefly algorithm, Friction stir welding.

The synthesis of materials in the applications is investigated and researched continuously, in order to bring out the better material proportion and condition to better suit the intended purpose. The origin of alloys from the monolithic materials or metals was only due to that search. Nowadays, the focus is on the design of materials and manufacturing processes with the purposes of effective workability, durability, economical design and so on. All these purposes need the optimization tools since they rely on the maximization/minimization /optimal solutions with respect to the intended use. Optimization of resources for any activity is much required for their effective utilization.
Optimization in the manufacturing sector is very important since every manufacturing process involves few process parameters that control the output of the processes. For instance, welding of two different materials through a joining process produces the weld strength of different degrees with respect to the type of welding.
Fusion welding, Adhesive bonding and riveting are conventionally used for the joining of components in aircrafts. Rivets are preferred in lap joining of sheets in aircrafts due to its inherent property of withstanding the stress without damage [1]. It is still the favourite method of joining the sheets in aviation industry although it is affected largely by stress concentration and fatigue. Fatigue analysis of the riveting operation on the dynamic conditions is carried out extensively in the literature [2-4]. Wronicz et al. [5] investigated the FEM analysis of M28 Sky truck aircraft. The work suggested the use of forces as boundary conditions rather than the displacements.
Based on the study of the joining of aircraft structures, better materials and manufacturing processes are being evolved over periods. Several optimization techniques are used conventionally to find the better process parameter setting which provides better joining processes. Tamilanban et al. [6] worked on the Taguchi technique, one of the widely used optimization techniques, to arrive better optimized values of parameters in stir casting of Al-SiC composite. Girimurugan et al. [7] employed Response surface methodology for the optimization of parameters of pure Aluminium AA1100. The relation between the factors and response are established using a mathematical model and the tensile strength is predicted. Pandiyarajan et al. [8] used desirability approach route for finding the optimized tensile strength of welded AA 6061-ZrO2-C composites.
Few algorithms are inspired from the nature so that their inherent properties are derived to the programming part to model the optimization problem. Genetic Algorithm is one such algorithm that is essentially the simulation of evolution theory. As the conventional optimization tools search from a defined start point, GA operates from the random location through the strings. This increases the robustness of the solution [9]. GA is used nowadays for the complex applications from the traditional approaches such as Vehicle Routing, Travelling Salesmen, Bin packing problems etc., in the earlier days [10-12]. Krishnan et al. [13] investigated the tensile properties of the Aluminium matrix hybrid composites (SiC and Al₂O₃) through Genetic Algorithm. The results are obtained through the simple convergence of the optimized results, thus providing the better process parameter setting. Canyurt et al. [14] studied the tensile strength of the laminates made by E-glass/vinyl ester is verified with the through the non-linear models through GA. Genetic Algorithm is coupled with the other search tools in order to increase the probability of success in attaining the solutions. The convergence of the solutions gets increased for the applications when GA is coupled with the other algorithms. Javadi et al. [15] utilized a hybrid technique of GA with ANN to find the converging rate of the solutions and confirmed the same in their work.
Su et al. [16] employed the GA-Neural network to test the gait patterns of the patients with discomfort in walking and arrived the better gait pattern. In the manufacturing sector, GA proves to be an efficient tool for scheduling the resources in an efficient way. Jia et al. [17] investigated the best combinations of factories for the job production and prepared better schedules using GA with Gantt Charts.
Firefly algorithm (FA) is a recent technique used in the optimization problems that has the inspiration from the nature. It is considered to a one of the techniques using Swarm Intelligence for identifying the best design point in the design space [18]. The adaptability of the firefly algorithm to the real-time problems is studied and experimented by a number of works in the literature. Senthilnath et al. [19] investigated the comparison of FA with the other nature inspired algorithms namely Artificial Bee Colony and Particle Swarm Intelligence in their work and found that the FA is more efficient.
Many variants of FA are used in the literature in order to get the optimal solutions in a better way for the applications. Cauchy Jump was used in the work carried out by Wang et al. [20] which was named as Random attraction Firefly Algorithm (RaFA) to converge the results sooner. The proposed work is focused on the optimization of the weld strength through the Coupled GA and FA model in order to get a better manufacturing alternative for riveting in aircraft structures through artificial intelligence.

Composites preparation
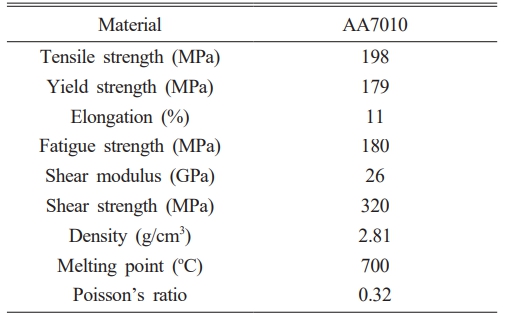
The effectiveness of the proposed optimization technique is adjudged from the experimental study of the strength of the welded composite samples. For this, the composite samples are fabricated with the following materials: Aluminium7010 (AA7010), Silicon Carbide (SiC) & Aluminium oxide (Al₂O₃). AA7010 is the major element, known as matrix, for the fabrication of composite material; along with the minor elements SiC& Al₂O₃, known as reinforcements that are used for rendering strength to the composite material. The compositions of matrix AA7010are provided in Table 1, which are confirmed from the chemical analysis method. The physical properties of the matrix Aluminium alloy AA7010 are shown in Table 2.
The AA7010 material is cut into billets and SiC & Al₂O₃ are prepared into powder form for the fabrication of hybrid composite material that is composed of two reinforcements. Weight percentage of the hybrid composite plays a major role in its strength. From the literature, it is found that the optimal weight percentage composition of reinforcements for the particulate composite ranges from 10% to 25% [21]. Each 10% of weight percentage for ceramic reinforcements SiC and Al₂O₃ is taken. AA7010 billets are taken in a graphite crucible and kept for melting in Muffle furnace in the temperature range of 720-750 ^oC. Meanwhile, ceramic powders are taken in another crucible to preheat to 900 ^oC for one hour in order to remove out the moisture content, which would form weak bonding. In the molten state of AA7010, the preheated ceramic powders are mixed with the help of vortex stirrer gently. Wettability between the matrix and reinforcements is improved by the wetting agent Mg by adding 1% weight percent. The uniform molten mixture is poured in a steel mould of dimensions 50 mm × 50 mm × 8 mm to obtain the samples. The temperature difference between the mould and molten metal may cause defects during heat dissipation and solidification. So, preheating of the mould to 250 ^oC is required.
Friction stir welding
Friction stir welding process (FSW) is relatively a new technology of joining metals by the mechanical forces, stirring and pressure, in order to create friction between the faying surfaces of the materials to be joined. The process is carried out in the temperature range just below the melting point of the base material. Hence it is also termed as Solid state welding process. Earlier the process is used for joining the light weight materials such as Aluminium, Magnesium etc., After the improvisation of the process by the researchers worldwide, it is extended to join the heavy materials such as Copper, steel etc., The machine used for the welding process of hybrid composites is shown in Fig. 1. It is a vertical milling machine with the indigenously attached fixture of FSW. The cylindrical tool with pentagonal pin (Fig. 2) of required dimension is attached with the spindle which rotates and traverses between the faying surfaces of the base materials with the application of pressure in order to create friction during the stirring action. The heat produced during the process is capable of producing pasty like plastic stage of material. The stirring action mixes both the materials together and the weld joint is obtained after solidification.
The molded samples of hybrid composite after solidification are taken to friction stir welding process for joining. The fixture for holding the specimens is shown in Fig. 3. The samples before and after the welding are shown in Fig. 4 & Fig. 5. Initially the hybrid composite samples are surface grounded in grinding machine to obtain the uniform surface for welding.
The current study is concerned with the optimization of tensile strength of the welded material. The tensile strength of the specimens is obtained by conducting the tensile testing of the specimens with ASTM standard E8 as shown in Fig. 6. The welding parameters such as tool rotating speed (RS), weld traverse speed (WS) and axial pressure (AP) are selected in the range 1050-1400 rpm, 22-50 mm/min and 1.2-4 kN respectively based on the literature. L27 orthogonal array design of Taguchi technique is used for the design of experiments. The tensile test is carried out for the 27 welded specimens to record the ultimate tensile strength of the weldments. The samples after tensile testing are shown in Fig. 7.

The objective of this work is to determine the best optimal values for the FSW process parameters that maximize the tensile strength of the Aluminum matrix composite material using a novel methodology that uses Genetic Algorithm and Firefly algorithm. The proposed work combines the advantages of both the algorithms. Genetic Algorithm is one of the best methodologies to search the global maxima in a design space through cross-over and mutation operators; whereas Firefly Algorithm is best suited for searching the best settings through local maxima. Many research works are performed in the past with the conventional optimization methodologies such as Taguchi etc., The complexity of the problem keeps on increasing with the dynamic nature of the factors included in the problem. To keep up with the pace of getting the right solution for the optimization problems, it becomes necessary to search for the novel technique that combines the features of a tool/algorithm with that of another. The ease with which the solution to arrive depends on the effective addressing and utilizing of the factors in the technique under study.
Genetic algorithm
Genetic Algorithm (GA) is an effective search algorithm influenced by the Darwin’s theory of natural evolution. GA is basically a metaheuristic tool which offers the optimal solutions in a population through search-and-find technique. This utilizes random search option rather than a set of defined principles/theory as in heuristics, in order to find the best/optimal results in the given set of members of population. Therefore, GA always presents the best solution in the sense that the solution obtained is either the optimal or near-optimal.
Firefly algorithm
Firefly Algorithm (FA) is one of the recent techniques in meta-heuristics for solving the optimization problems. The characteristics of firefly flash patterns are simulated in the algorithm to find the hidden points for optimization (optimal design points). It was proposed by Xin She Yang in 2008, which is designed to mimic the features of firefly in the optimization problems in order to obtain the best optimal setting of parameters. The algorithm is based on a set of agents (fireflies) that search for the optimal points in the vast design place. The local search is initiated at different locations in random fashion by the fireflies that search for the best points locally according to the fitness function. The fireflies are attracted to each other by the flashing pattern. The bright firefly attracts the dull firefly irrespective of the gender. The assessment of the brightness of the fireflies is executed till all the fireflies are compared, in order to obtain the global optimal point.
Methodology to solve the optimization problem
Any problem that involves the prediction of maximization/minimization/optimality points through the tested method; and that is reproducible in terms of the iterations is termed to be the Optimization problems. The proposed method is used to find the maximized weld strength in terms of tensile property. The algorithm is designed in two phases: In phase I, GA is used to select the better chromosomes from each set of iterations through cross-over and mutation. These chromosomes represent the best class of fit considering the objective functions, which are taken to a different set of pool. In phase II, FA is used to find the best point from the same pool of chromosomes through the operators such as light intensity etc, thereby getting the best out of best. The methodology is programmed in MATLAB environment to facilitate the easy iteration among the large population. The results are obtained through visual means (Plots) to get the best optimal point of weld strength. The pseudo code for the proposed methodology is given in Table 3.

Genetic algorithm
Setting of parameters
The design problems require the design constraints in order to get the finer results. The parameters for GA need to be fixed for the effectiveness of the model employed for the search.GA requires the fitness function to get started. The fitness function is arrived from the regression equation of the experimental analysis of tensile testing of 27 welded samples. The fitness function is similar to the regression equation except the terminology given. The terminology for regression equation is the desired output (Ultimate tensile stress, in this case) in terms of the inputs (axial force, rotation speed and weld speed), whereas for GA, the term ‘Fitness function’ is provided as shown below:



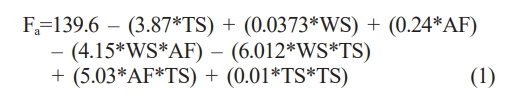
Few parameters are set with the standard values and few others are varied to get the better fitness values. As mentioned earlier, the design space for the experiment is set with the help of the process parameters used in GA. The design space is extended with reference to the capabilities of the machine tool used for the experiments part. The design point which is feasible in the setting in machine tool is only used for every process parameter. In order to utilize the 4-bit storage system for the algorithm, 15 levels of the process parameters are assigned. Table 4 shows the different parameters and their values to be used in Genetic Algorithm. The 4-bit binary coding system is used to designate the codes of the members in the design space.
Population pool generation
The generation of population pool is the initial step to start the algorithm. It is generated for the cross-over and mutation operations through three steps: (i) Random call-over (ii) Probability of repetition (iii) String allocation. Random call-over of any 10 codes (Parents) is executed from the entire population to start the GA process. The program in MATLAB is designed to call any random values with 3 sets of 4 bit binary code from the population space for selecting the parents, as shown in Table 5. The random coding from 0001to 1111 are selected as the chromosome for the Population pool generation for a process parameter. Thus, the code 000100010001 account for the first setting of each parameter. The bit assignment for the process parameters are shown in Table 5. The chromosomes for the corresponding process parameters are shown in Table 6.
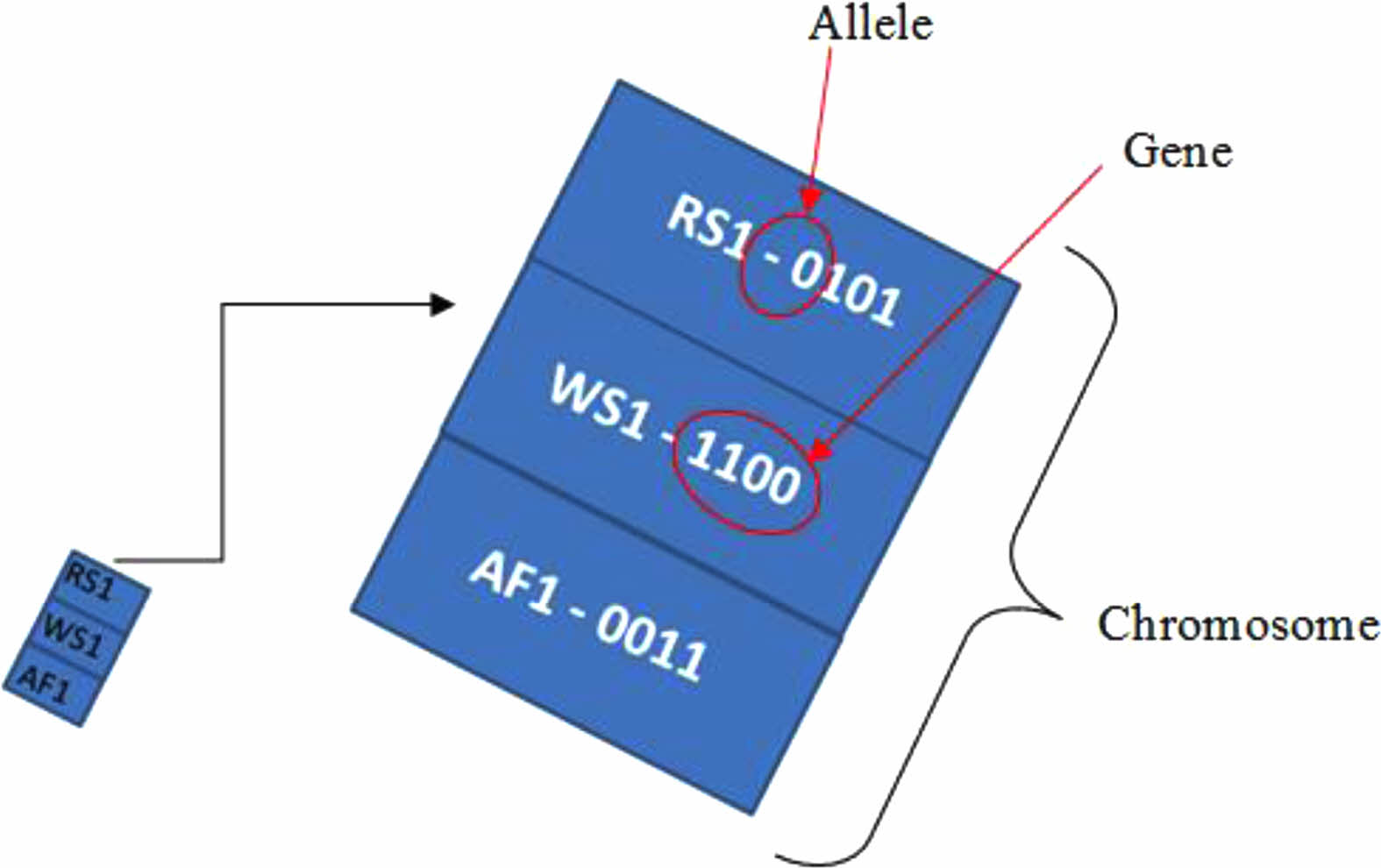
The formation of chromosomes for the algorithm is designed from allele to gene. An allele, as shown in Fig. 8, corresponds to a digit in the four bit binary code. For a process parameter, 4 digits are combined together to form a gene. Three genes are clubbed together for a chromosome for a setting of run in the optimization. Thus, a chromosome is responsible for 12 alleles and 3 genes, genes being process parameters and alleles being levels of each parameter.
The population pool is initiated in random fashion during the first phase. Fig. 9. shows the population pools generated as Parents 1 and 2. The calculation of the objective function is carried out with every chromosome using the formula as given earlier. The next phase, Probability of repetition, is characterized by the selection of the best 80% of the population pool. Then, the string allocation is done through cross-over and mutation steps, in order to get the optimal chromosome for the prediction of maximized tensile strength of weldments.
The probability of repetition of good parents is attained by the prediction of the Random number from the Cumulative Probability of the corresponding value.
Pool for cross-over
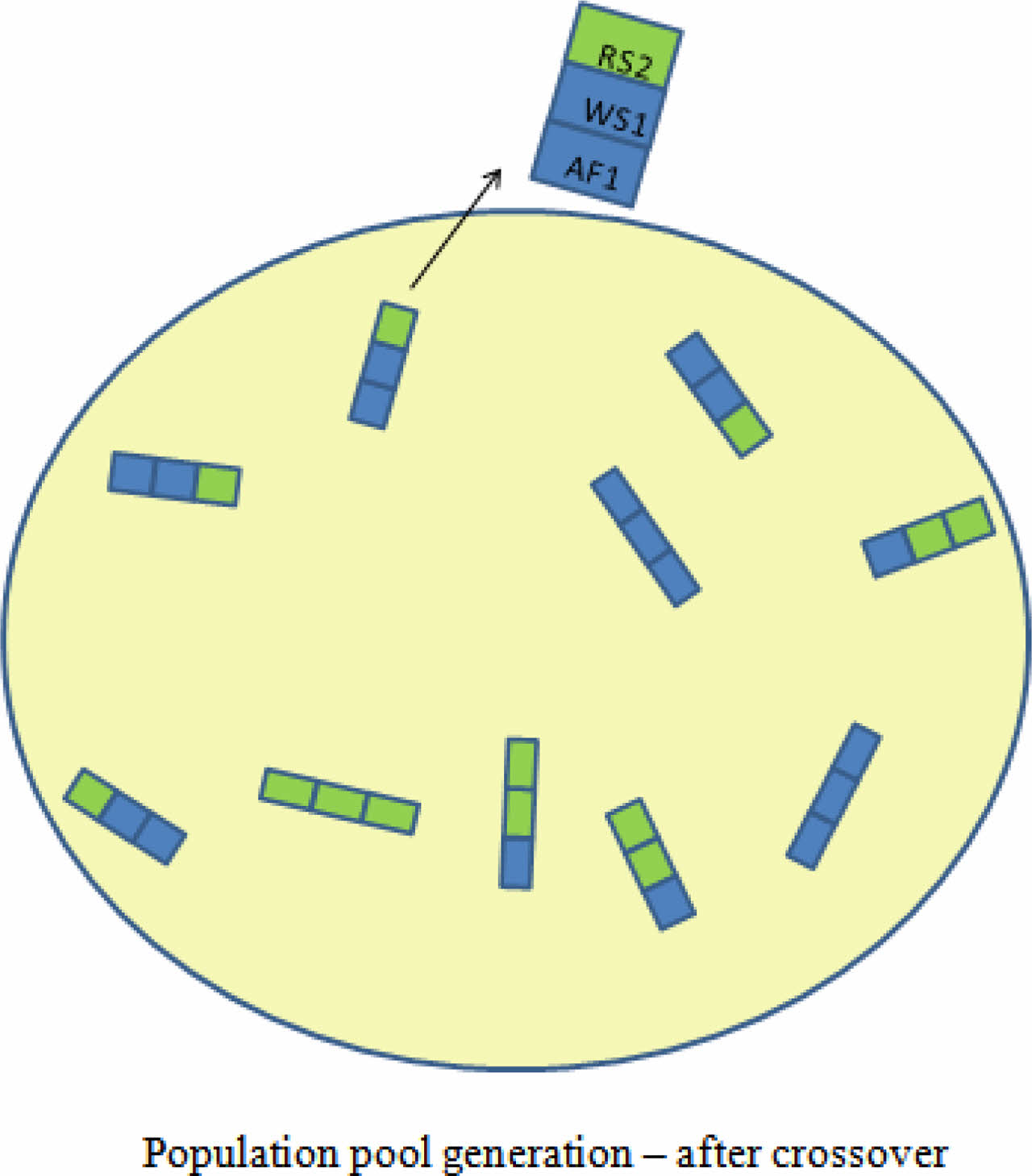
The top 80% offspring from the random selection for each parent are taken to the cross-over phase. Cross-over is programmed to occur at the end of the first gene or the second gene. As shown in Fig. 10. the cross-over of both parents is performed in the program and the new offspring are developed at the end of cross-over in a single pool. A representation of chromosome is shown clearly depicting the crossover site after the first gene. The first gene of Parent 2 is clubbed with the other two genes of Parent 1, as RS2-WS1-AF1.
Pool for mutation
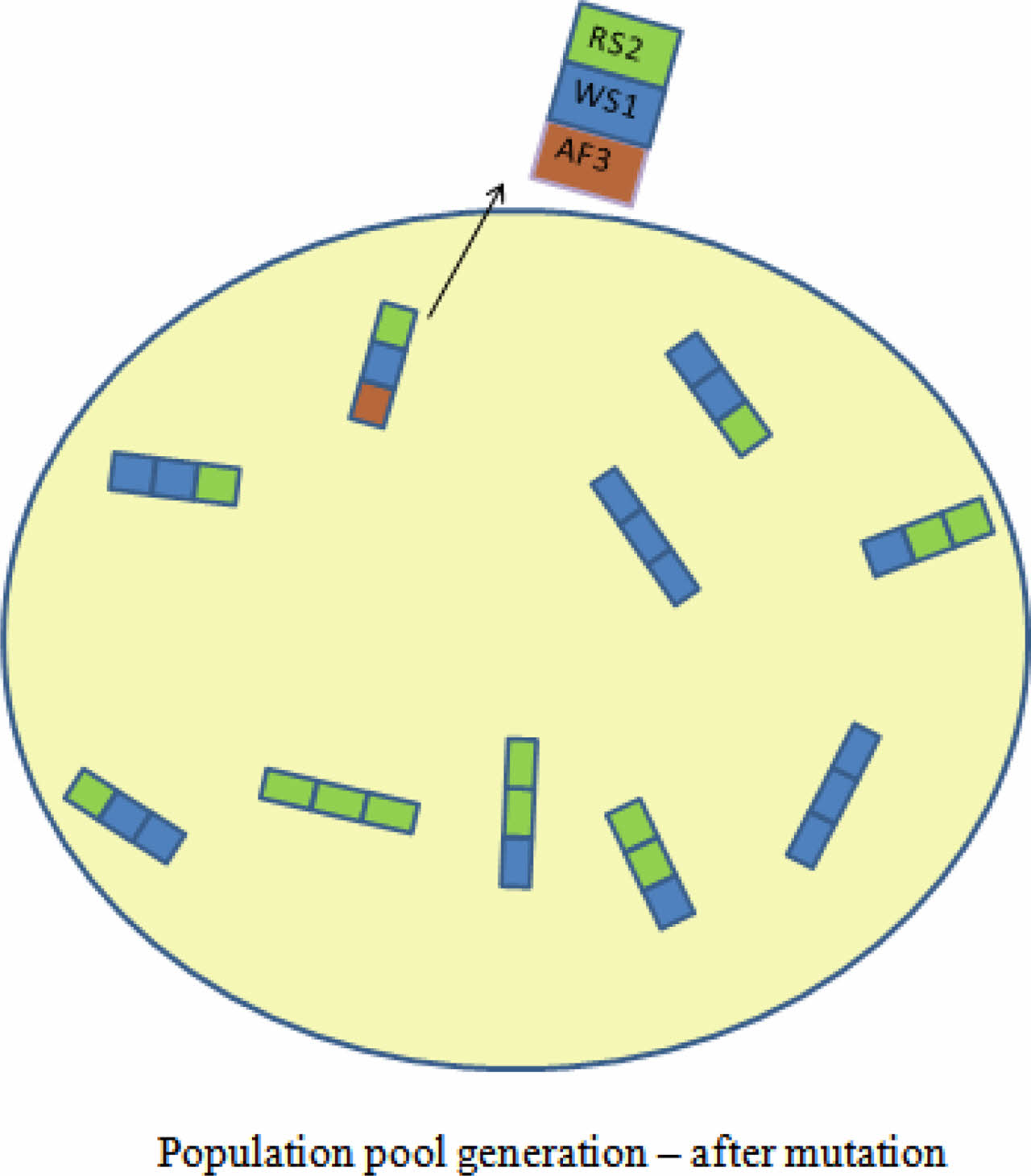
Mutation phase is applied to the crossed over offspring in the second stage. The representation given in Fig. 11 shows that one allele (AF3) out of the entire population pool is changed, in order to get the new variety of the chromosomes. Mutation is responsible for the exploration of new varieties of offspring by altering only an allele. The formula for finding the number of alleles to change for mutation is,



Thus, mutation is carried out in 6 bits for a population size of 10 chromosomes and 12 alleles. Thus, the chromosome after mutation (RS2-WS1-AF3) along with other top chromosomes passes to the next phase of the algorithm.

Determination of optimal points
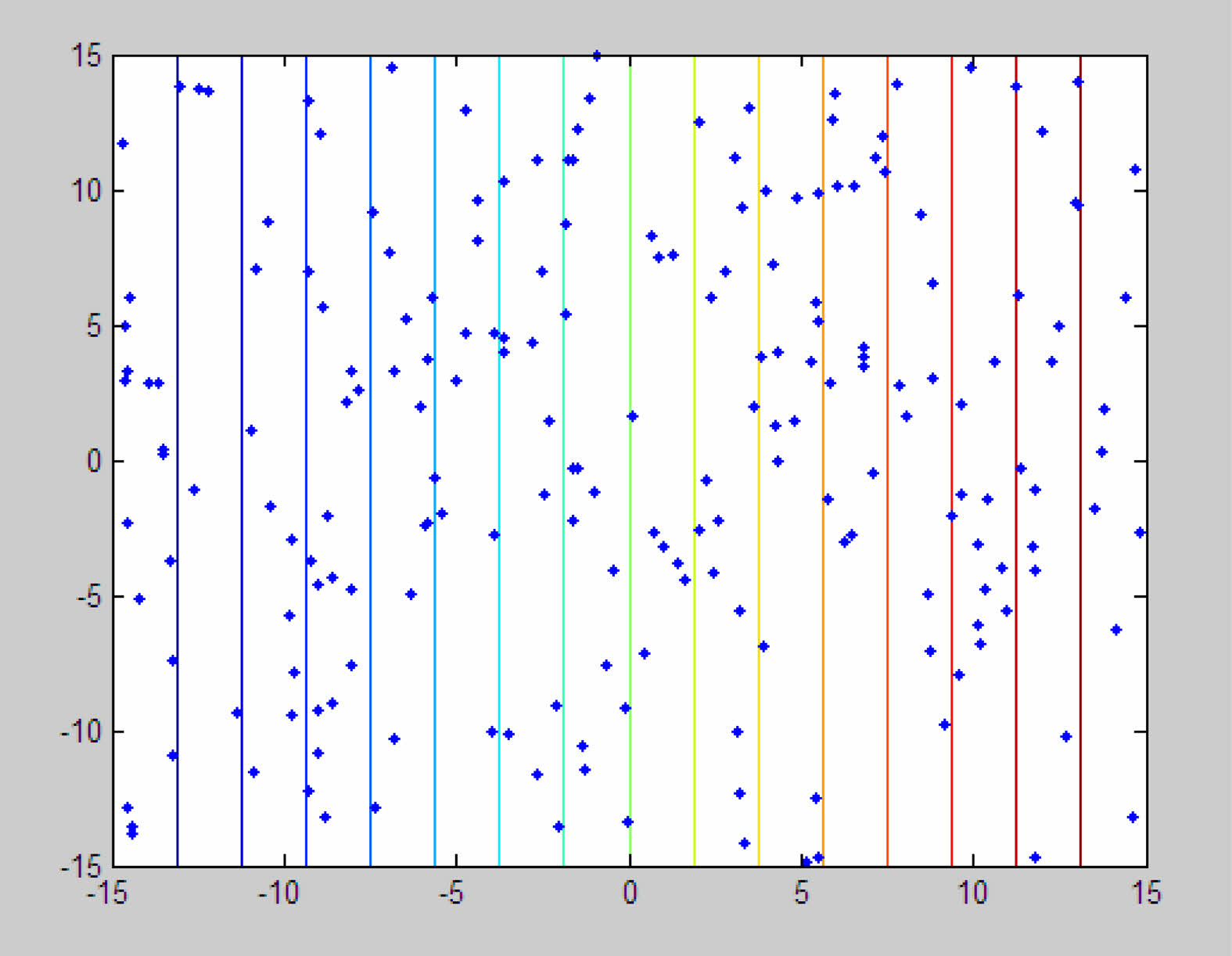
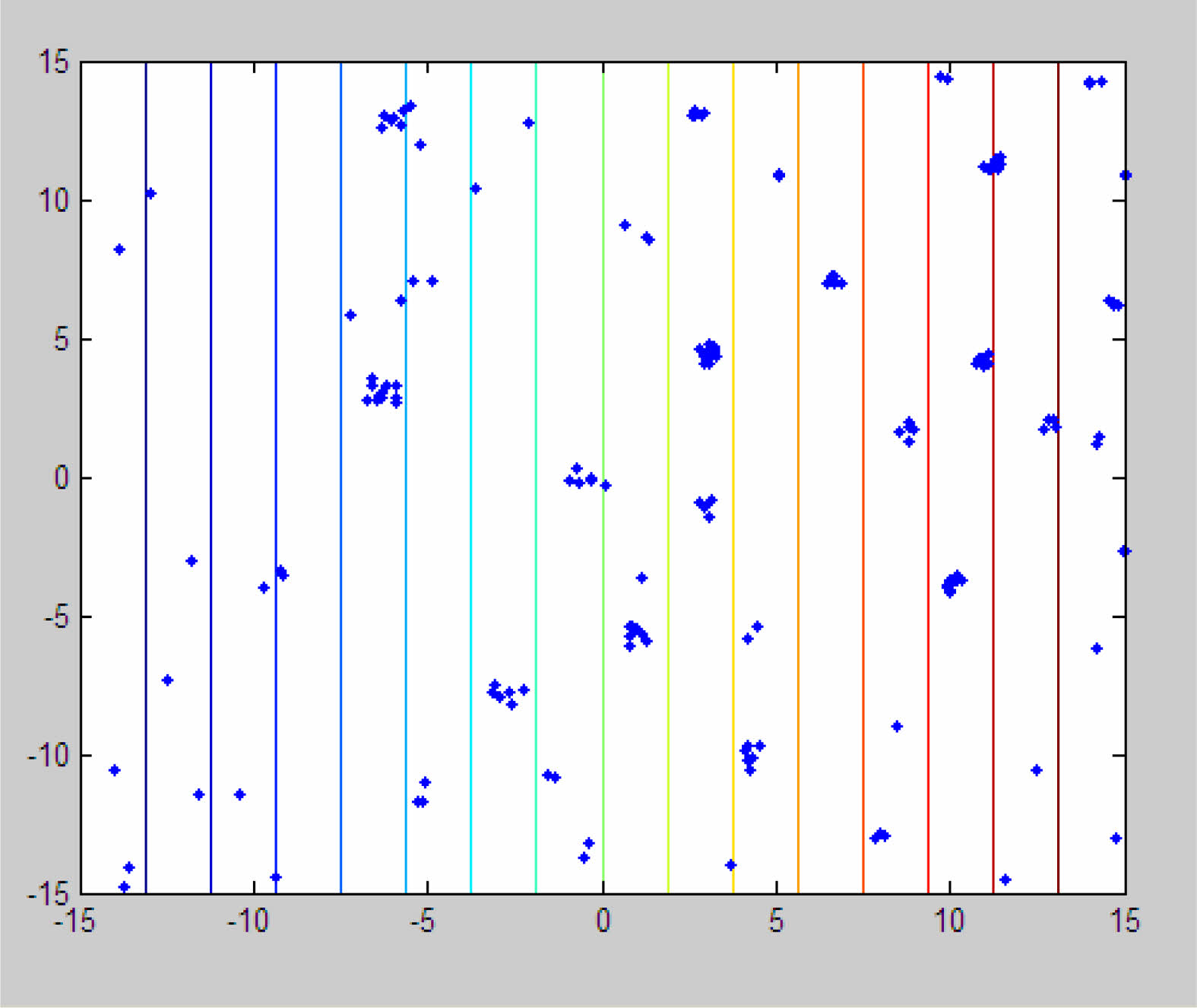
The outputs obtained from the MATLAB tool are shown in Fig. 12 & Fig. 13. Before the FA execution, the flies are seen distributed in the design space, whereas after the analysis execution is done, the flies move towards the nearby best solution. The algorithm is so designed such that the fireflies exploit the nearby local optimized design points and tend to agglomerate towards them. Once the local best values are agglomerated, the exploration of the best out of local bests (i.e. Global best) is carried out. Thus, the optimized process parameter setting in the selected design spaces is obtained through Firefly Algorithm. FA is capable of converging towards the optimized values by ignoring the majority of noise values, unlike Genetic Algorithm. In Fig. 13, the fireflies are scattered in the design space before the start of the search of optimal points. As the execution of the program is started the fireflies tend to move to their nearest and brightest counterparts, from which the design point with the best parameter setting will get the maximized strength. The final destinations of the fireflies are shown in Fig. 14, after the local and global searches are carried out.
Genetic Algorithm iterates for all the population and collects the best results for every iteration. But Firefly uses the exploration and exploitation search techniques for the local best values obtained from the Genetic Algorithm. Thus, the advantages of both GA and FA algorithms are utilized in the suggested technique. In the programs executed only with GA and only with FA also fetch the better results of optimized values.
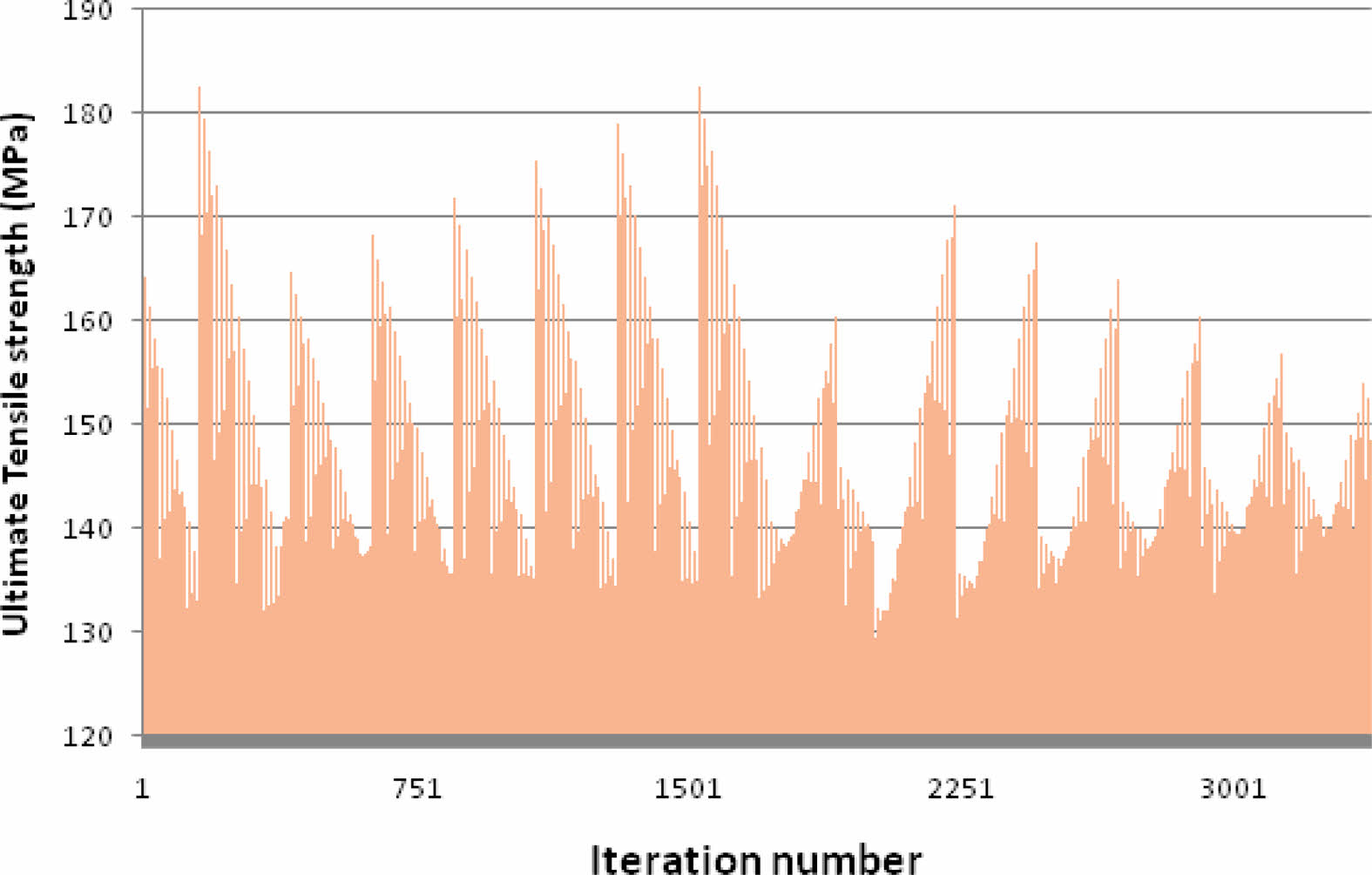
The tabulation of the ultimate tensile strength obtained for the iterations are shown in Fig. 14. The results show that every design point with different process parameter values tends to contribute to the strength of the weldments, either in small or large. The design points with comparatively maximum tensile strength are seen in different parts of the design space, indicating that the effective search algorithm is required to search out those points. The search optimization should be capable of moving from the local optimal points to get the global best point.
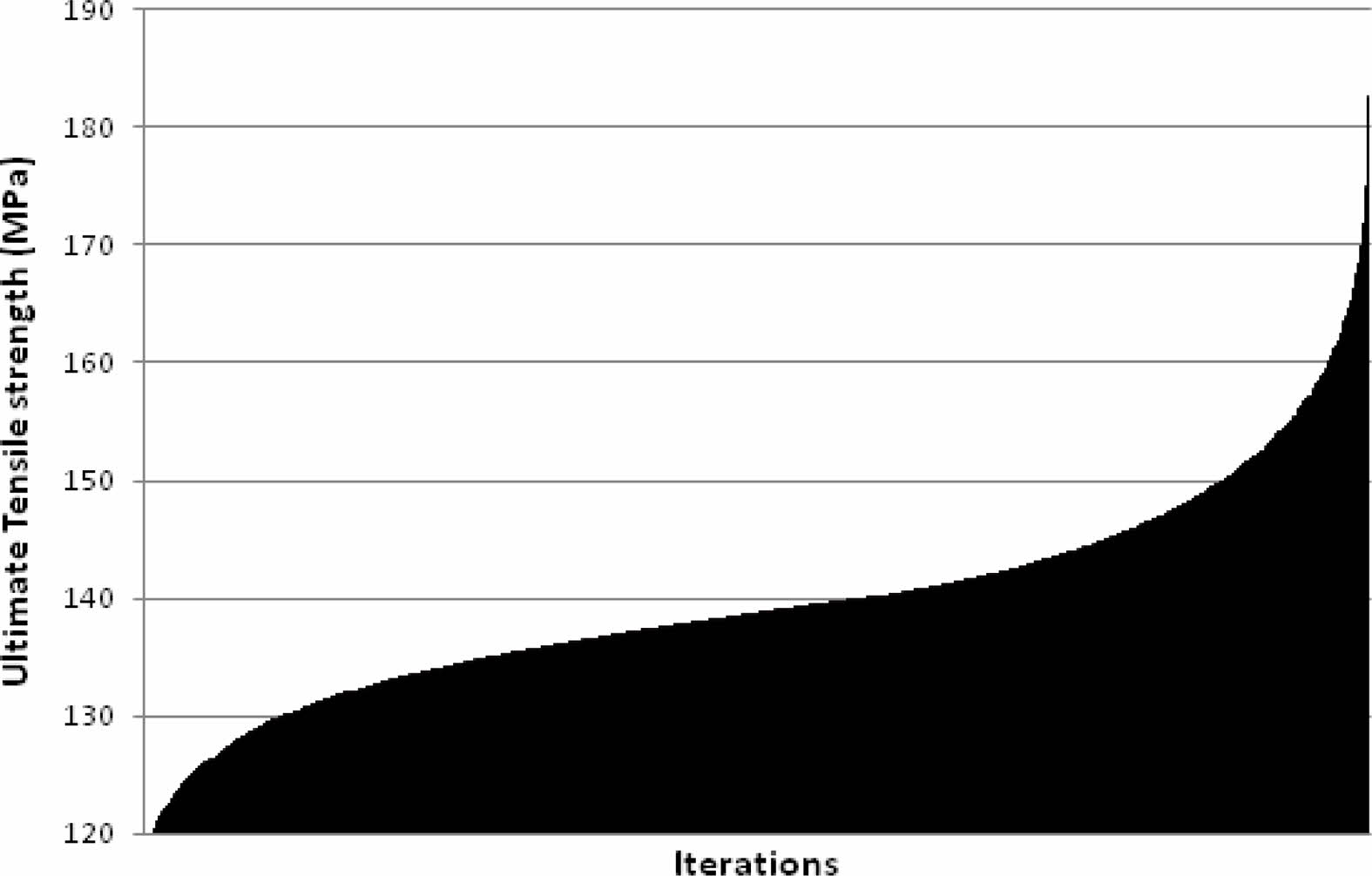
The distribution of the ultimate tensile strength values for the iterations is shown in Fig. 15. It is seen clearly that the strength ranges from 129 MPa to 189 MPa across all design points. It is correlated to the impact provided by the process parameters used for the optimization. The maximum strength point shows the value of 184.17 MPa in the prediction, which is confirmed with the experimental value of 175.50 MPa with the process parameter setting of TS –1400 rpm; WS –22 mm/min; AF –1.2 kN. From the iteration point of view, the best optimal points tend to vary for every execution, since the algorithms chosen belong to the metaheuristic approach. But, the strength of the optimal design points is searched out by the coupled GA-FA algorithm.

In this work, the optimization of the process parameters for the welding of composites is carried out through the coupled GA-FA algorithms using Matlab programmings. A mathematical regression equation is formulated from the tensile results of 27 weld samples. The validation of the regression equation is confirmed through analysis of variances (ANOVA). Two phases are used for the optimization: Genetic Algorithm (GA Phase) and Firefly Algorithm (FA Phase). The GA phase is employed with the objective of pool generation and selection of the best offspring from each iteration. The best offspring are stored in a new pool to get the optimal combination through FA phase. FA aims at the clustering of the fireflies at the best optimal solution through its procedures. The coupled GA-FA algorithm shows improved optimized results with best parameter setting. Since the algorithm developed is a part of metaheuristic domain, every final iteration of the result after the two phases showed results with slight variations as expected. The best optimal parameter setting is obtained with the following values: Tool rotation speed (TS) – 1375 to 1400 rpm; Weld traverse speed (WS) – 22 to 26 mm/min; Axial force (AF) – 1.2 kN to 1.4 kN.
The results of the proposed model is validated by conducting the real-time experiments in the machine, showing significant valediction with the predicted results with errors less than 5%. This coupled GA-FA algorithm utilizes the best features of both algorithms to predict the better design point in the given design space. The results showed that the coupled GA-FA algorithm outperformed the results of GA & FA utilized in the uncoupled single optimization tool.