- Study on the vibration characteristics of full ceramic ball bearings under low temperature working conditions
Jian Sun, Junran Huang, Zhonghao Tian, ZhongXian Xia*, Lu Wang and Yang Zhang
School of Mechanical Engineering, Shenyang Jianzhu University, Shenyang 110168, China
This article is an open access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
To better understand the vibration characteristics of full ceramic ball bearings operating under low temperature conditions and ultimately reduce vibration levels to improve their service life, a low temperature bearing test machine was utilized to analyze the dynamic characteristics of the bearings. Vibration measurements were taken to determine the vibration acceleration root-mean-square value of the full ceramic ball bearings under varying rotational speeds and loads. The results show that the vibration acceleration reaches up to 3.17865 m/s² at room temperature. At around -100 ℃, the vibration reaches the lowest point, which is only 0.65415 m/s². As the temperature decreases, the vibration decreases gradually, especially when the temperature drops below -20 °C, the vibration decreases sharply. It was found that as the rotational speed increased, so did the vibration acceleration of the bearings, while the vibration acceleration showed a trend of decreasing initially and then stabilizing with increasing load. By comparing and analyzing simulation and test results, the simulation model was optimized and a vibration model specific to full ceramic ball bearings was established. These findings provide a theoretical foundation for the use of full ceramic ball bearings in low temperature environments, offering valuable insights for reducing vibration and enhancing bearing longevity.
Keywords: Full ceramic ball bearing, Low temperature, Analog simulation, Vibration characteristics, Si3N4.
Bearings are the key basic parts in the field of industrial machinery, known as the "joints of equipment" [1]. With the continuous advancement of science and technology, bearings are increasingly being subjected to more demanding working conditions. Traditional metal ball bearings often fall short when faced with challenges such as wide temperature variations, corrosion, lack of oil lubrication, strong magnetism, and other harsh environments [2]. In contrast, full ceramic ball bearings represent a cutting-edge solution in the realm of high-tech bearing products, featuring rings and rolling bodies crafted from ceramic materials. These full ceramic ball bearings exhibit exceptional performance characteristics, excelling in areas such as high-speed operation, heavy load capacity, resilience to wide temperature ranges, corrosion resistance, electrical insulation, and resistance to magnetic fields [3-5]. As a result, they find extensive applications in industries ranging from aerospace, navigation, metallurgy, and chemical engineering to national defense and military sectors [6-8].
At present, domestic, and foreign experts and scholars have studied the friction vibration of full ceramic ball bearings based on the theory of metal ball bearings. Guan et al. [9] studied the vibration and temperature rise characteristics of all-ceramic ball bearings under high temperature conditions and conducted bearing vibration tests to simulate the high temperature environment. The vibration and temperature rise increase with the increase of speed, and the temperature rise change of all ceramic ball bearings is smaller than that of metal ball bearings. Guo et al. [10] studied the vibration law of 6206 silicon nitride ceramic bearings under different oil supply and axial loads and found that the contact load between the ball and the outer ring is larger than that between the ball and the inner ring under the same conditions. Zhang et al. [11] studied the dynamic characteristics of full ceramic ball bearings under ultra-low temperature conditions and established a model of liquid nitrogen lubrication of full ceramic ball bearings. Fang et al. [12] studied the distribution law of lubricating oil film of full ceramic ball bearing and established the mathematical model of elastic flow lubrication of full ceramic ball bearing, and the results show that the lubricating film thickness of full ceramic ball bearing is positively correlated with the rotational speed and negatively correlated with the load. Zhang et al. [13] conducted a study on the vibration characteristics of ceramic bearings under different temperatures, preloads, and rotational speeds. Their findings the significant impact of thermal deformation on the dynamic characteristics of the bearings. Guo et al. [14] developed a mathematical model for a five-degree-of-freedom rolling bearing using the control-variable method and investigated the dynamic changes in bearing clearance for full ceramic bearings at varying rotational speeds and radial loads. Ohta et al. [15] tested all-ceramic ball bearings with silicon nitride balls and rings and compared their vibration characteristics with those of hybrid ceramic ball bearings and conventional steel ball bearings. The vibration measurement results show that the overall vibration speed of the all-ceramic ball bearing is affected by the rotation speed and does not change with the axial load. Wu et al. [16] explored the influence of oil supply and preload on the vibration characteristics of silicon nitride full ceramic deep groove ball bearings. To verify the low-temperature adaptability of all ceramic ball bearings, Xia et al. [17] conducted experimental research on silicon nitride all ceramic ball bearings under extreme conditions and analyzed their frictional behavior and vibration characteristics. The results indicate that a self-lubricating film will form inside the bearing, becoming a lubricating medium, but at the cost of excessive wear on the retainer, indicating that the Si3N4 ring and ball have good adaptability to extreme conditions, and the retainer is a weak link that is prone to failure and damage. Wang et al. [18] Based on quasi-static bearing and oil film thickness theory, the influence of rotational speed on centrifugal force and oil film thickness of raceway center of different bearing materials was analyzed.The experimental results show that the vibration-effective value of the Si3N4-Si3N4 bearing is lower than that of the other two materials when the speed is higher. Grease lubrication slightly reduces vibration acceleration compared to oil-air lubrication. Zhang et al. [19] conducted dry friction tests and simulation studies on PEEK, CF30 and PVX cage silicon nitride full ceramic ball bearings. The test show that the transfer film has the effect of wear reduction and lubrication on the bearing.
In recent years, research on full ceramic ball bearings has primarily focused on room temperature, with limited studies on their performance at low or ultra-low temperatures. To address this gap, this study investigates the vibration characteristics of 6208CE silicon nitride full ceramic deep groove ball bearings at low temperature. Using the JH-200E low-temperature bearing tester, bearing vibration was measured to examine the impact of rotational speed, load, and temperature on the bearings' vibration levels. By comparing and analyzing simulation and test results, the simulation model was optimized, leading to the establishment of a vibration model for full ceramic ball bearings. This research sheds light on the vibration behavior of full ceramic ball bearings at low temperatures, offering valuable insights for reducing vibration, enhancing bearing performance, and extending their service life.
Hertz contact theory
The Hertz contact theory [20] is a fundamental concept in the dynamic modeling of steel bearings, crucial for analyzing and calculating the contact stiffness between bearing components. This theory is particularly valuable when considering the contact between elements as elastic contact in bearing dynamics. Even in full ceramic ball bearings, where contact deformation between elements remains within the elastic range, the Hertz contact theory proves useful for analyzing the dynamic characteristics.
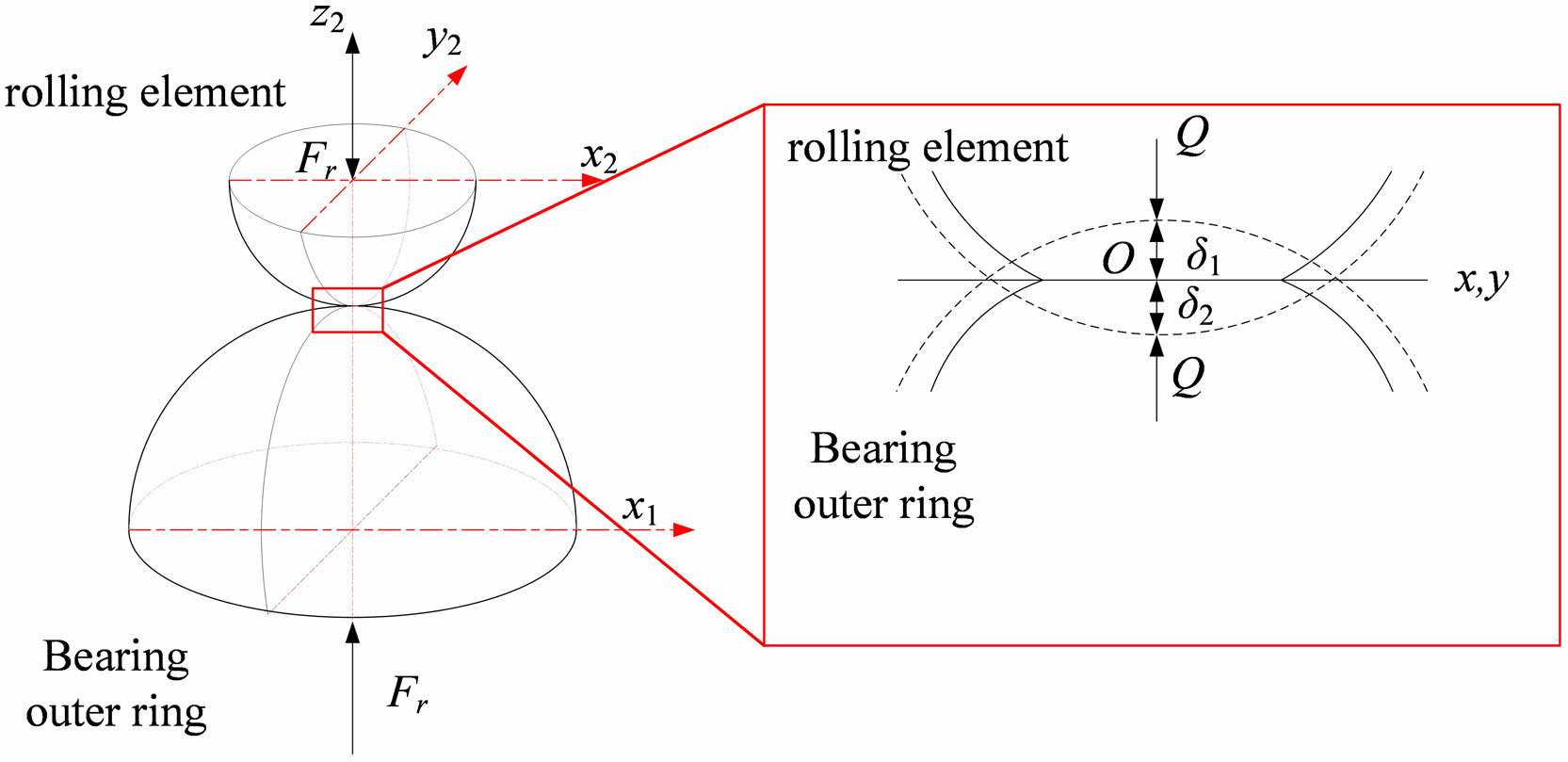
Figure 1 illustrates the contact between the rolling body and the outer ring of the bearing during the operation of a full ceramic ball bearing. When subjected to a radial force Fr, the contact surface between the rolling body and outer ring experiences elastic deformation.
The deformation δ at the contact surface between the rolling element and the outer ring of the bearing can be expressed as
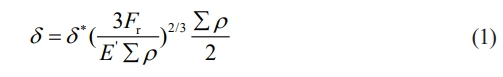
where Σρ is the curvature sum, E’ is the equivalent elastic modulus.
The contact pressure can be expressed as
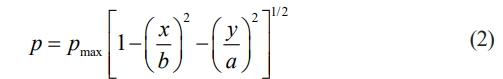
Where a and b are the long and short semiaxes of the contact ellipse, respectively, pmax is the maximum contact pressure.
The relationship between contact deformation and contact load can be obtained under the condition of elastic contact occurring between the elements:

According to the point contact deformation formula, the Hertz contact deformation stiffness KH in the point contact region is calculated as
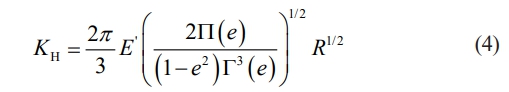
Since the ceramic material is less deformed under the same force, the force deformation is calculated for silicon nitride and steel materials, respectively, and it is known that the deformation of silicon nitride material is 67.7% of that of steel material under the same force condition. Therefore, equation (4) is corrected to get.
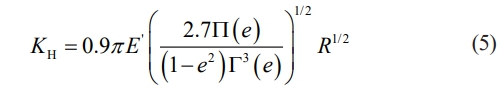
where Γ and Π are full elliptic integrals of type I and type II, respectively.
Differential equation of vibration
Calculate the contact deformation between the rolling body and the collar by considering the contact between the rolling body and the inner and outer rings of the bearing as two different radii of spheres in contact. the contact deformation is
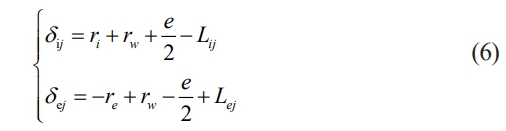
Where δij and δej are the contact deformation between the rolling element and the inner and outer rings of the bearing, respectively; ri and re are the inner raceway radius and outer raceway radius, respectively; rw is the radius of the rolling element, e is the radial clearance of the bearing, and Lij and Lej are the distances between the centers of the rolling element and the centers of the inner and outer rings, respectively. Lij and Lej can be expressed as follows
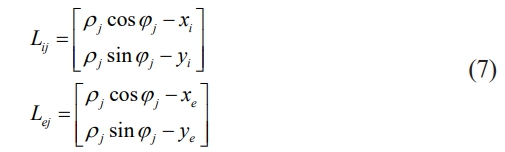
where ρj is the radial distance between the center of the fixed coordinate and the center of the rolling element, rm is the bearing pitch diameter, ρj = rm + rj.
By applying the Newtonian kinematics equation, the differential equation of motion between the components of the bearing can be derived. Specifically, the differential equation of motion for the inner ring can be obtained.
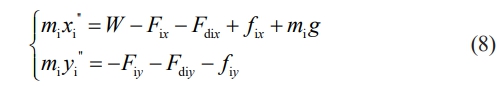
where mi is the mass of the inner ring, W is the external radial load applied, and fi is the friction of the inner ring. The equation of motion of the outer ring is.
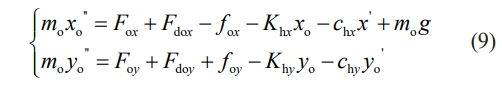
Where mo is the mass of the outer ring of the bearing, Km is the stiffness of the outer ring and housing, chx is the damping of the outer ring and housing, and fo is the friction of the outer ring.
The differential equation for the motion of the cage in the direction of rotation is.
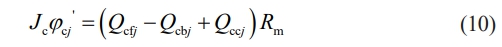
Where Jc is the cage moment of inertia and Q is the contact force.
The differential equation of motion of the rolling element of the bearing is given by.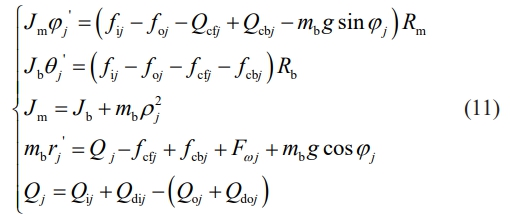
|
Fig. 1 Schematic diagram of point contact. |
Test equipment
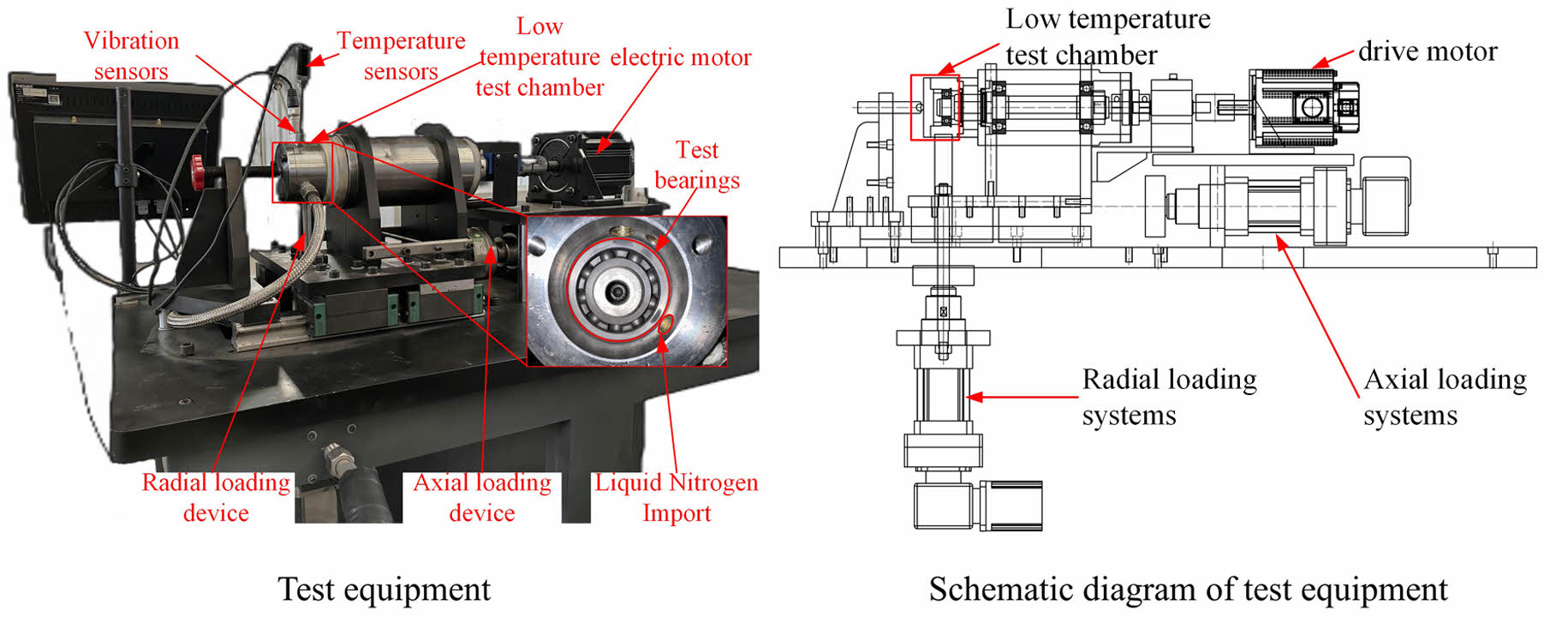
JH-200E Low Temperature Bearing Tester is specially designed for bearing performance testing in low temperature environment with advanced technology and precise control. The tester depicted in Fig. 2 guarantees the uniformity and reliability of the test chamber's temperature by employing servo control of the temperature sensor and flow control valve. Additionally, it is furnished with a contact vibration measuring device to precisely gauge the vibration levels of the bearing's outer ring, offering a dependable foundation for subsequent data analysis. Throughout the testing process, the contact vibration measuring instrument captures temperature and vibration of the test bearing's outer ring, storing them efficiently on the computer for future reference. These data can be monitored and subsequently processed in real time through the software system, providing important support for bearing performance analysis and optimization.
Test program
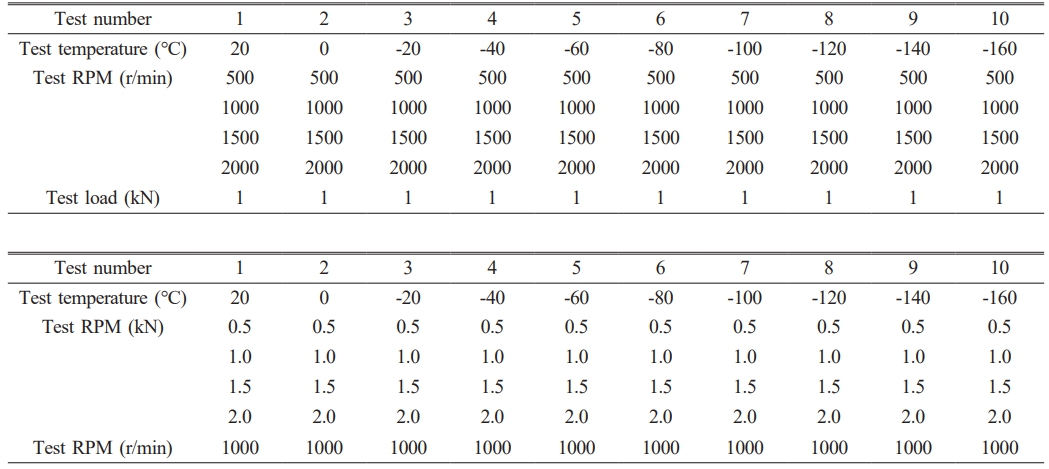
The test was carried out from room temperature to ultra-low temperature process, different temperatures under the bearing vibration test, but also in one of the temperatures, different loads and different rotational speeds bearing vibration test. low-temperature bearing test program as shown in Table 1. From room temperature to low temperature, respectively, different temperatures under the test. At the same time, experimental research was conducted on the vibration of bearings at different speeds and loads at a temperature of -100 ℃.
|
Fig. 2 Test equipment and schematic diagram. |
Effect of temperature on bearing vibration
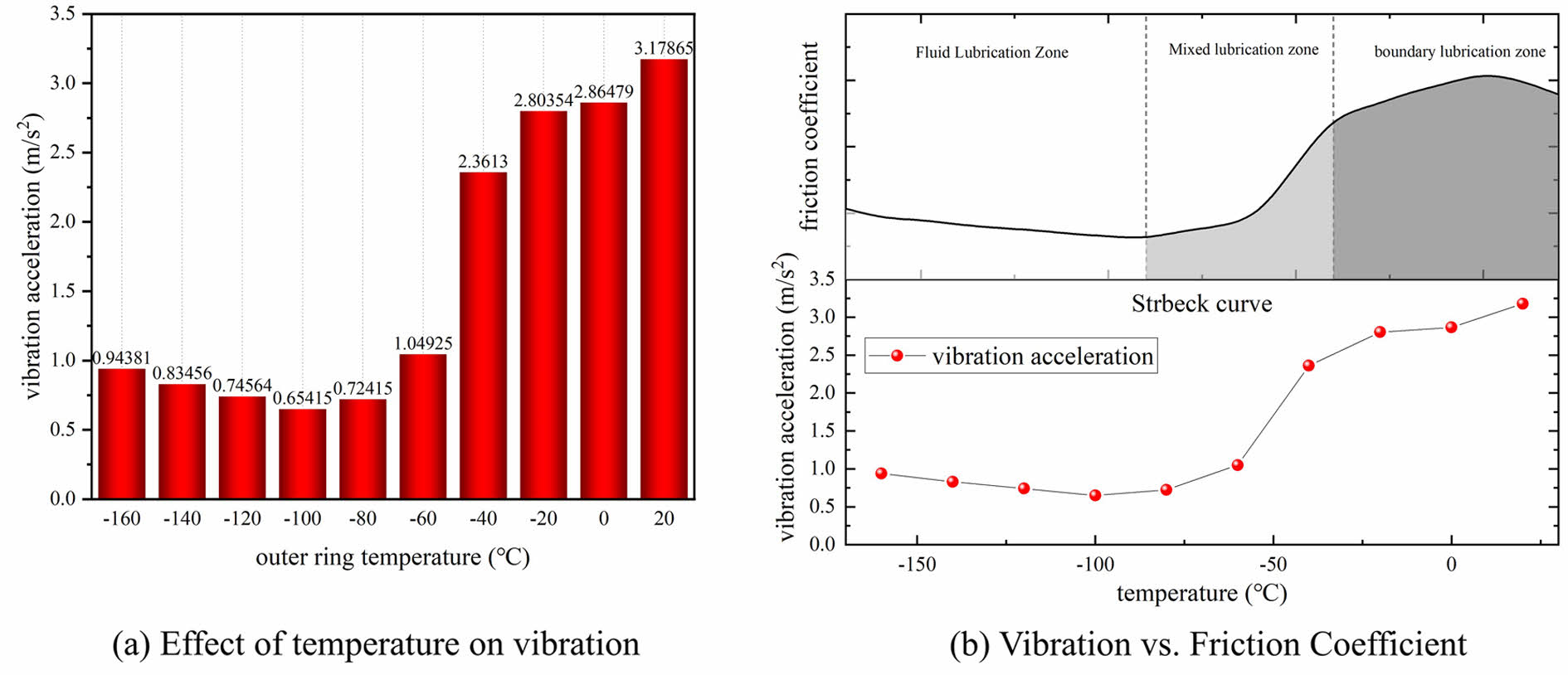
To investigate the vibration characteristics of full ceramic ball bearings under varying temperature conditions, a series of low-temperature tests were conducted. The results, as depicted in Fig. 3(a), reveal intriguing insights. Under different working conditions, the bearing vibration acceleration shows different characteristics. At room temperature, the vibration acceleration is up to 3.17865 m/s². As the temperature decreases, the vibration gradually decreases, especially when the temperature drops below -20 ℃, the vibration decreases sharply. At around -100 ℃, the vibration reaches a minimum of 0.65415 m/s². Subsequently, the vibration rises slightly and stabilizes at around 1 m/s². To avoid the bearings from "locking up", bearings with a clearance of class C3 were used.
As the test chamber temperature decreases, the presence of liquid nitrogen gradually increases, infiltrating the bearing and forming a lubricating film. This film effectively separates the ceramic balls from the inner and outer ring grooves, providing lubrication and reduce vibrations. With further temperature reduction and higher liquid nitrogen content, the effect of the liquid film intensifies, leading to a notable decline in bearing vibration acceleration. However, once the liquid nitrogen content reaches a certain threshold, the vibration reduction effect of liquid film is limited, stabilizing the vibration acceleration. Subsequent temperature drops result in reduced bearing clearance, elevating the contact stress between the ceramic balls and the inner and outer rings. This heightened stress intensifies collisions, slightly increasing vibration acceleration.
In Fig. 3(b), a comparison between the bearing vibration acceleration test results and the friction lubrication curve of the bearing reveals a similarity in trends. As temperature decreases and liquid nitrogen content rises in the test chamber, the lubrication state transitions from boundary to fluid lubrication. The formation of a lubricating film by liquid nitrogen in the bearing contact area diminishes collisions between the rolling elements and the rings, reducing contact forces and effectively lowering bearing vibration acceleration. This shift achieves the desired outcome of mitigating bearing vibrations.
Influence of different working conditions on bearing vibration
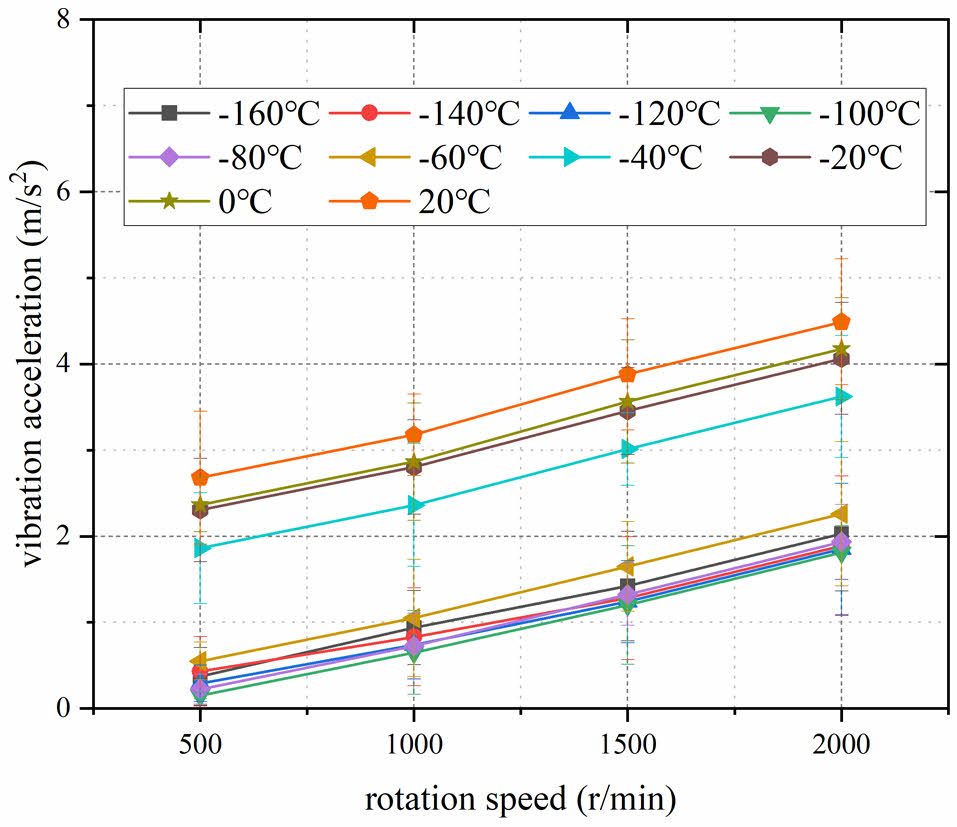
To investigate the effect of different speeds on the vibration of all-ceramic ball bearings in a low-temperature environment, tests were conducted at different speeds under the test conditions of T = -100 ℃ and radial load Fr = 1.0 kN, and the test results are shown in Fig. 4. The results show that in the low-temperature environment, the vibration acceleration of the bearing increases with the increase in bearing speed. This is because as the rotational speed increases, the contact stress between the ceramic balls and the grooves of the inner and outer rings increases, leading to increased friction between the ceramic balls and the grooves, which in an increase in the vibration acceleration of the bearing. Additionally, as the rotational speed increases, the overall heat generation of the bearing increases, causing the temperature inside the bearing to rise, which affects the liquid nitrogen content in the test chamber, resulting in changes in the distribution of liquid nitrogen inside the bearing, and subsequently affecting the bearing vibration.
It is also important to note that the vibration of full ceramic ball bearings is more stable under low-speed conditions. This is because the contact stress between the ceramic balls and the inner and outer raceways is small at low speeds, resulting in lighter collisions between the bearings and the inner and outer raceways, leading to lower vibration acceleration values. On the other hand, under high-speed conditions, the contact stress between the ceramic balls and the inner and outer raceways is higher, leading to more intense collisions between the ceramic balls and the inner and outer raceways, resulting in higher vibration acceleration values.
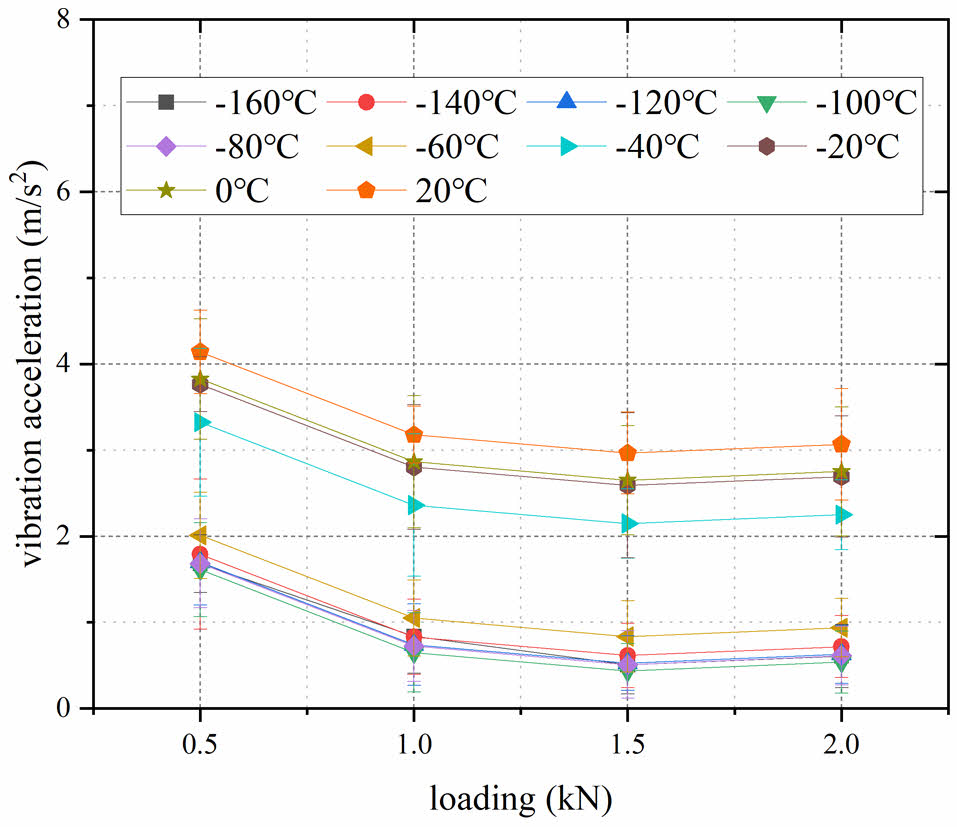
To further understand the effect of load on bearing vibration, tests and analysis were conducted on bearing vibration under different loads at T = -100 ℃ and speed n=1000 r/min conditions, and the test results are shown in Fig. 5. In the low-temperature environment, the vibration acceleration of the bearing shows a tendency to decrease and then stabilize with an increase in load. This phenomenon may be due to the restriction of the motion state of the ceramic balls in the bearing as the load increases. With an increase in load, the collision between the ceramic balls decreases, leading to a decrease in the vibration acceleration of the bearing. However, as the bearing load increases further, the overall heat generation of the bearing also increases. This increase in heat generation may affect the distribution of the liquid lubrication film, causing the lubrication damping effect to be somewhat affected. Therefore, after the load is increased to a certain level, the vibration acceleration of the bearing tends to slightly increase as the load continues to increase.
|
Fig. 3 Bearing vibration and lubrication status. |
|
Fig. 4 Bearing vibration at different speeds. |
|
Fig. 5 Bearing vibration under different loads. |
Modeling of bearing vibration
In the process of dynamic modeling of rolling bearings, the components of rolling bearings are often viewed separately, and the differential equations of motion are established to realize the real-time simulation of the operating state of the bearings. Due to the complexity of the rolling bearing contact problem, the following conditions are set to simplify the bearing, ignoring the minor factors that have less influence on the vibration, so the following assumptions are made for the bearing [21]:
(1) The balls are uniformly distributed with respect to the shaft.
(2) The movement of the balls on the raceway surface is pure rolling.
(3) Only the forces on the bearing in the radial direction (in the X, Y plane) are considered.
(4) The contact between the balls and the raceways conforms to the Hertz contact conditions.
(5) The stiffness and damping due to the lubricant are neglected.
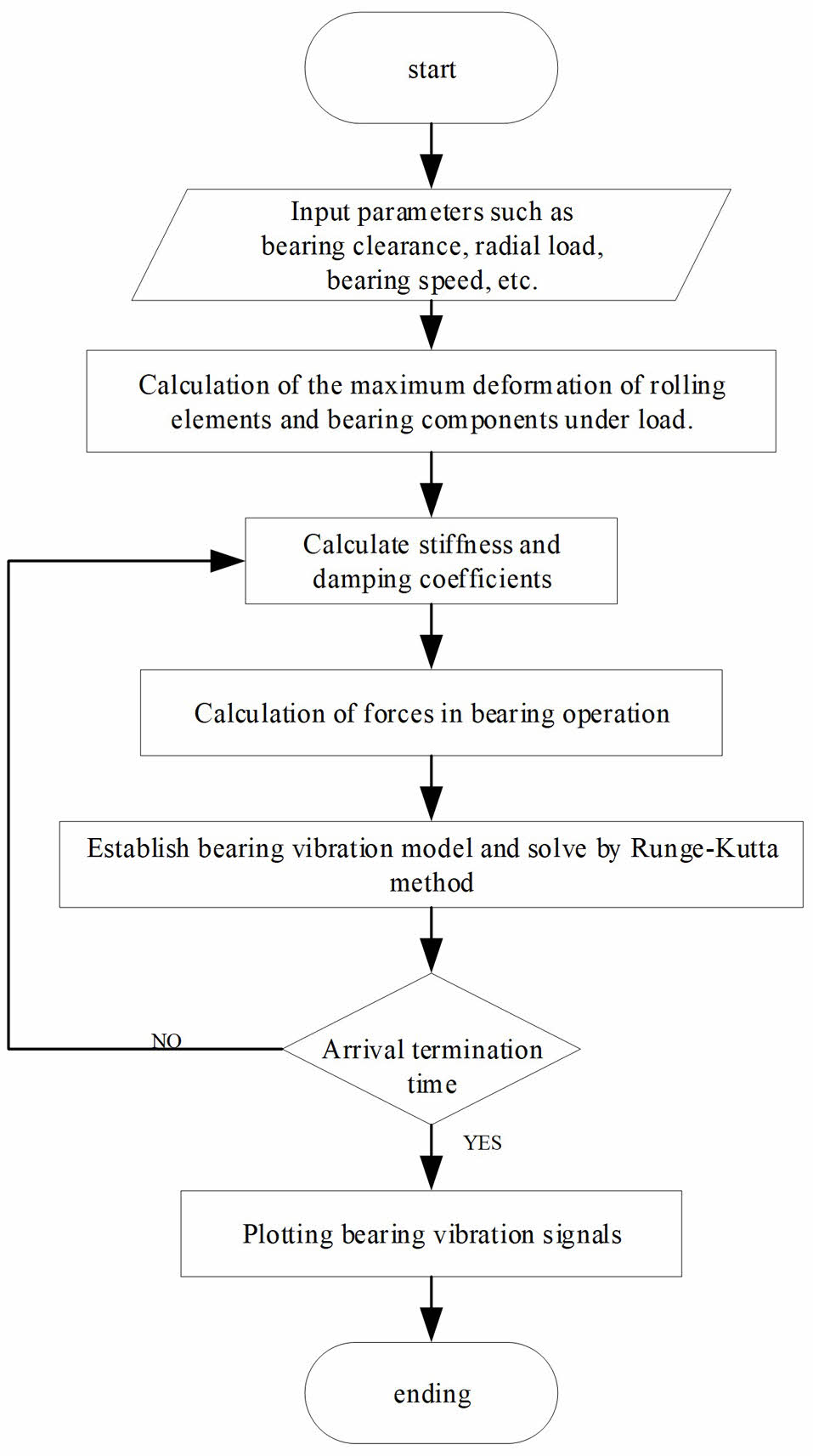
The established theoretical model was simulated by numerical simulation software, and the program flow was designed. The basic idea of the algorithm was shown in Fig. 6. The vibration equations composed of ternary second-order ordinary differential equations can be solved by Runge-Kutta algorithm in numerical simulation software. For the ordinary differential equation dy(t)/dt=f(t,y(t)), yn is the left endpoint, yn+1 is the right endpoint, tn is the starting point of the time value of each step, tn+1 is the end point of the time value of each step, h is the step length, four functions are used in the estimation of each step, and the estimated function f (t), The y value of the desired solution is then obtained by adding the linear combination of these f-values to the left end point of the function value yn.
Bearing Simulation Results and Analysis
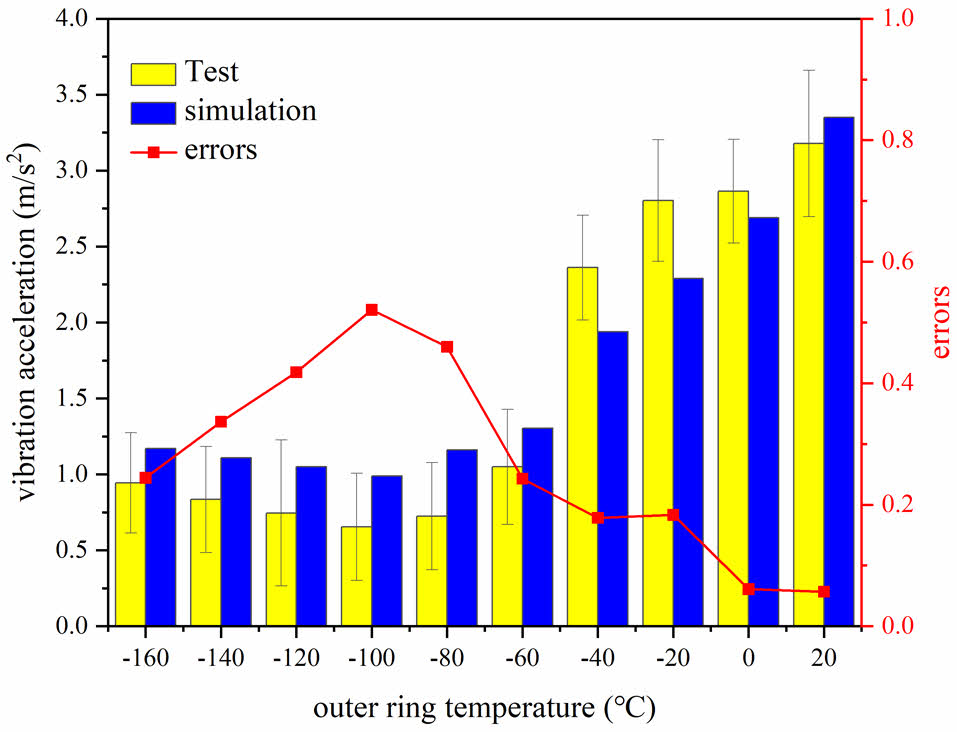
The simulation results of bearing vibration acceleration were obtained by conducting multiple sets of simulations at different temperatures, comparing them with test results, as shown in Fig. 7. As the bearing clearance decreases, the vibration simulation results for full ceramic ball bearings initially decrease and then slightly increase, consistent with the test results and confirming our hypothesis.
Upon further analysis, it was observed that the vibration acceleration simulation values of the bearing decrease as the temperature changes from 0 to -100 °C. However, the decrease is slightly smaller compared to the test results, with a significant relative error of up to 50%. This discrepancy can be attributed to the formation of a liquid lubrication film in the test using liquid nitrogen, which dampens vibrations. This factor was not considered in the numerical simulation, leading to differences between the simulation and test results.
In order to improve the accuracy of the simulation results, future simulations should take into account the presence of a liquid lubrication film and it reduce on vibrations. This will help reduce the relative error and improve the overall reliability of the simulation results.
Optimization of bearing simulation parameters
The presence of the liquid film reduces the contact stiffness between the rolling elements and the inner and outer rings, leading to a decrease in the natural frequency of the bearing system. If you want to get accurate bearing vibration simulation results, you need to carry out the calculation of the equivalent integrated stiffness of the contact zone of the bearing in a suitable way.
When the bearing is in a low-temperature environment, there is a liquid film in the contact area of the bearing, and the stiffness of this liquid film is
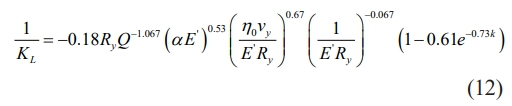
where, k is the ratio of the long and short half-axes of the contact ellipse; α is the coefficient of viscous pressure; Ry is the equivalent contact radius in the direction of motion, η0 is the coefficient of kinetic viscosity of the liquid; and vy is the velocity of coiling suction.
Then, based on the series model, the total stiffness of the contact zone is

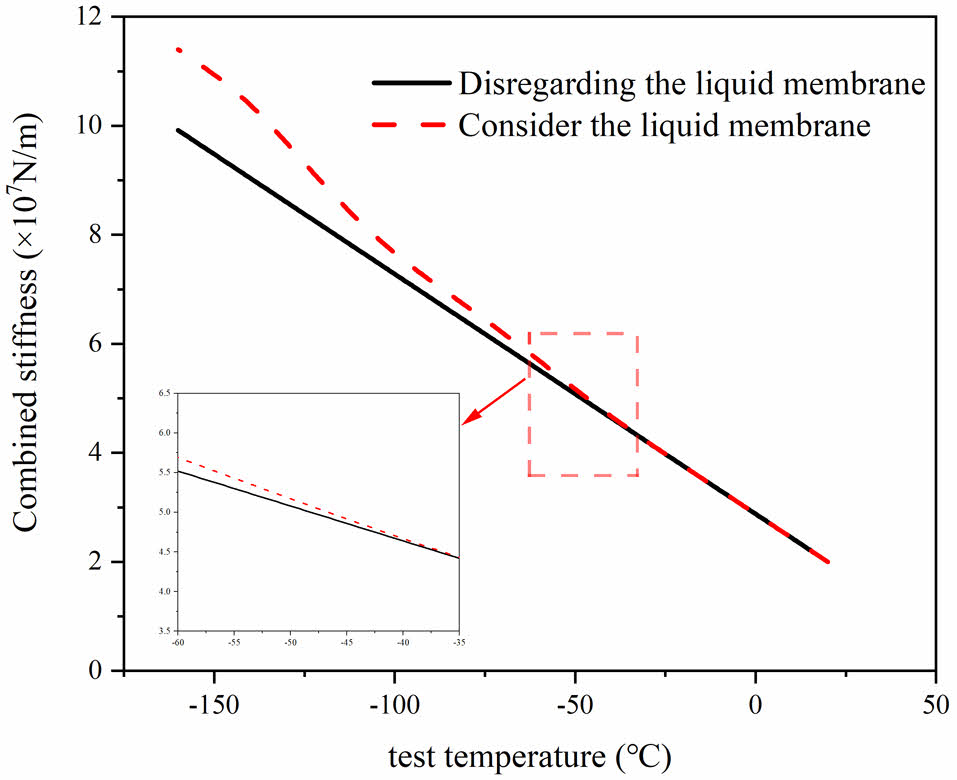
The curve illustrating the variation of bearing test temperature on its radial integrated stiffness is depicted in Fig. 8. It shows that the radial integrated stiffness of the bearings increases as the temperature decreases. Interestingly, at higher test temperatures, the trend of radial integrated stiffness remains consistent for bearings with and without a lubrication film. However, when the temperature falls below -40 °C, the combined radial stiffness of bearings with lubrication film surpasses that of bearings without lubrication film.
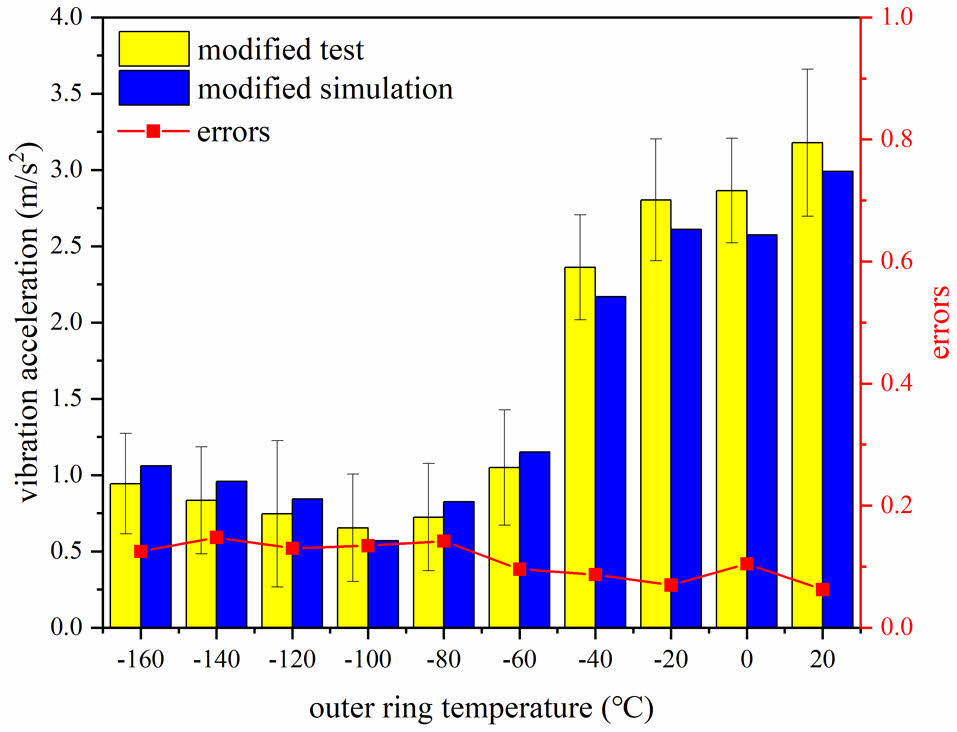
Incorporate the corrected radial comprehensive stiffness into the bearing vibration simulation program, as shown in Fig. 9. To enhance the accuracy of the simulation results, the simulation model was comprehensively corrected. The corrected model takes into full consideration of the material, geometric parameters and lubrication conditions of the bearing and other factors that affect the actual work. After comparison with the test data, we find that the error between the corrected simulation results and the test results is significantly reduced, with the maximum error not exceeding 15%. Compared with the previous mathematical calculation model, the accuracy is improved by about 70%. This result not only verifies the effectiveness of our optimized simulation model, but also provides strong support for the optimization of bearing vibration performance.
After optimization, the results of the effects of load and rotational speed on the vibration acceleration of the bearing are presented in Fig. 10. It is evident that as the bearing speed increases, the vibration acceleration of the bearing also rises. As the radial load on the bearing increases, the vibration acceleration initially decreases before stabilizing, aligning with the test results.
The simulation result plots clearly indicate that the impact of rotational speed on the vibration acceleration of the bearing is more pronounced. As the rotational speed rises, the vibration acceleration also increases, demonstrating a positive correlation. On the other hand, the influence of load on vibration acceleration is relatively minimal, with only slight changes observed even as the load varies.With the increase of load, the stiffness of liquid film also increases, and the effect of rotational speed is vice versa. The increase of liquid film stiffness leads to the decrease of bearing vibration, so the change of load has relatively little influence on the bearing. This finding is consistent with the test results, further validating the accuracy and reliability of the simulation model.
|
Fig. 6 Numerical simulation flow of bearing. |
|
Fig. 7 Vibration simulation of bearing with different clearances. |
|
Fig. 8 Comparison of radial integrated stiffness of bearings before and after optimization. |
|
Fig. 9 Comparison between simulation and test of the corrected bearing vibration. |

|
Fig. 10 Simulation results of bearing vibration under different working conditions. |
The study of full ceramic ball bearings under normal, low, and ultra-low temperature conditions has been meticulously conducted, focusing on the influence of temperature variations on vibration characteristics under varying rotational speeds and loads. By establishing a mathematical model for vibration acceleration in full ceramic ball bearings and integrating test data with simulations, the following key findings have been deduced:
(1) The test outcomes reveal a pattern where the vibration acceleration of full ceramic ball bearings decreases initially with decreasing ambient temperature, eventually stabilizing, and in some cases, experiencing a slight increase. At lower temperatures, subtle changes in the internal structure may impact the vibration characteristics. The vibration acceleration escalates with higher rotational speeds, underscoring the significant influence of speed on bearing vibrations. As the load increases, the vibration acceleration of the bearings tends to decrease before stabilizing. This trend is attributed to load variations affecting internal stress distribution and contact conditions, consequently impacting vibration characteristics.
(2) The numerical simulation method was employed to analyze the test results to deeply investigate the influencing factors of bearing vibration acceleration with temperature variations. The study revealed that while the numerical simulation results were largely in line with the test results, some disparities were observed. These differences could be attributed to the incomplete consideration of the impact of the liquid film on the vibration damping properties of the bearing at low and ultra-low temperatures. Particularly at low temperatures, the formation of the liquid film was found to significantly influence the vibration characteristics of the bearing. However, the vibration damping capacity of the liquid film was constrained by the low viscosity of liquid nitrogen. Further reduction in temperature might introduce additional factors affecting the bearing vibration acceleration, potentially leading to a slight increase.
(3) Overall, the research highlighted that temperature exerts a substantial influence on the vibration acceleration of full ceramic ball bearings, with rotational speed ranking next in significance, while load has the least impact. This discovery holds significant implications for comprehending the behavior of full ceramic ball bearings across diverse operational settings and serves as a valuable reference for future investigations. Subsequent research endeavors could focus on enhancing the performance of full ceramic ball bearings through material enhancements, structural design optimizations, and a comprehensive exploration of the liquid film's effect on the bearings' vibration characteristics.
Future research can focus on improving the performance of full ceramic ball bearings through material improvement. At extreme temperatures, the usual grease and oil lubrication will not be applicable, so we believe that materials with self-lubricating properties can reduce bearing vibration and increase bearing life.
In future studies, the structural design of full ceramic ball bearings will be optimized to enhance the overall bearing performance. Such as radial clearance, inner and outer ring groove curvature radius, ball diameter, ball number and so on.
National Natural Science Foundation of China: Research on lubricant film characteristics and discriminating mechanism of multi-field coupling all-ceramic ball bearing based on elastohydrodynamic lubrication, No.: 52105196; Department of Education of Liaoning Province Project: Study on Multi-factor Coupling mechanism and inhibition method of Micro-cracks in Channel surface of all-ceramic ball bearing, No.: LJKMZ20220936; Young and middle-aged innovative talents in Shenyang: high-precision all-ceramic ball bearings for CNC machine tool spindles, No.: RC210343.
- 1. L. Wang, R.W. Snidle, and L.Gu, Wear. 246[1-2] (2000) 159-173.
-

- 2. P. Cento and D.W. Dareing, Tribol. Trans. 42[4] (1999) 707-714.
-

- 3. W. Harrer, M. Deluca, and R. Morrell, Eng. Failure Anal. 36 (2014) 262-268.
-

- 4. B. Su, C. Lu, and C. Li, Machines. 12[8] (2024) 510.
-

- 5. P.M. Lugt, M.T. Zoelen, C. Vieillard, F. Berens, R. Gruell, G. Preisinger, and Meaney, P. Tribol. Trans. 65[1] (2021) 1-13.
-

- 6. X. Bai, H. Zheng, Z. Wang, and Z. Wang, Shock and Vib. 2021[1] (2021) 6650798.
-

- 7. H. Shi, M. Hou, Y. Wu, and B. Li, Int. J. Control, Autom. 20[3] (2022) 727-740.
-

- 8. H. Shi, M. Hou, Y. Wu, and B. Li, International Journal of Control, Autom. 20[3] (2022) 727-740.
-

- 9. J. Sun, R. Guan, J. Yao, X. Fang, Z. Zhang, and G. Zhang, High Temp. Mater. Processes. 28 (2024) 27-45.
-

- 10. J. Guo, Y. Wu, X. Zhang, H. Wang, X. Bai, Y. Zhang, and H. Lu, Lubr. Eng. 48[7] (2023) 0150-0254.
- 11. J. Sun, G. Zhang, Z. Xia, Z. Bao, J. Yao, X. Fang, Z. Zhang, and R. Guan, Ind. Lubr. Tribol. 75[4] (2023) 432-47.
-

- 12. J. Sun, X. Fang, J. Yao, Z. Zhang, R. Guan, and G. Zhang, Ind. Lubr. Tribol. 75[8] (2023) 919-932.
-

- 13. K. Zhang, Z. Wang, X. Bai, H. Shi, and Q. Wang, Adv. Mech. Eng. 12[1] (2020) 1687814020903851.
-

- 14. J. Guo, Y. Wu, X. Zhang, Y. Zhang, H. Wang, X. Bai, and H. Lu, Adv. Mech. Eng. 14[7] (2022) 16878132221109349.
-

- 15. H. Ohta and S. Satake, J. Trib. 124[3] (2002) 448-460.
-

- 16. Y. Wu, J. Guo, X. Zhang, Y. Zhang, H. Wang, X. Bai, J. Sun, and H. Lu, Int. J. Adv. Manuf. Tech. 127[9] (2023) 4943-4957.
-

- 17. Z. Xia, Y. Wu, T. Ma, Z. Bao, J. Tian, L. Gao, J. Sun, and S. Li, Tribol. Int. 175 (2022) 107849.
-

- 18. Y. Wang, S. Li, C. Wei, Y. Zhang, G. Lin, D. An, and J. Zhao, J. Ceram. Process Res. 25[4] (2024) 643-659.
-

- 19. J. Sun, Z. Zhang, Z. Xia, X. Fang, R. Guan, G. Zhang, and J. Yao, J. Ceram. Process Res. 24[3] (2023) 541-553.
-

- 20. F. Kong, W. Huang, Y. Jiang, W. Wang, and X. Zhao, A Shock Vib. 2018[1] (2018) 5424875.
-

- 21. B.J. Hamrock and D. Dowson, J. of Tribol. 99[2] (1977) 264-275.
-

 This Article
This Article
-
2024; 25(6): 975-984
Published on Dec 31, 2024
- 10.36410/jcpr.2024.25.6.975
- Received on Jul 3, 2024
- Revised on Sep 11, 2024
- Accepted on Oct 24, 2024
 Services
Services
- Abstract
introduction
full ceramic ball bearing vibration equation
test equipment and programs
test results and analysis
numerical simulation of bearing vibration conditions
conclusion
prospect
- Acknowledgements
- References
- Full Text PDF
Shared
 Correspondence to
Correspondence to
- ZhongXian Xia
-
School of Mechanical Engineering, Shenyang Jianzhu University, Shenyang 110168, China
Tel : 13719021640 - E-mail:






 Copyright 2019 International Orgranization for Ceramic Processing. All rights reserved.
Copyright 2019 International Orgranization for Ceramic Processing. All rights reserved.