- Examining the impact of sintering conditions on the microwave dielectric properties of Ca0.61M0.26TiO3 (M=La3+, Nd3+)
Chun-Hsu Shen*, Chih-Hsuan Hu, Jing-Yuan Chen, Wen-Hui Chen, Chen-Wei Tung, Yun-Hsien Yang and Ting-Yu Yang
Department of Electronic Engineering, Ming Chuan University, 5 De Ming Rd., Gui Shan District, Taoyuan City 333, Taiwan
This article is an open access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
This research, which takes a unique approach, investigates the influence of calcination temperatures on the microwave dielectric properties of Ca0.61M0.26TiO3 (M=La3+, Nd3+) ceramics. The samples were prepared using a conventional solid-state reaction method, with systematic variations in calcination temperatures. The sintering process, a crucial step in sample preparation, was conducted at a sintering temperature for a duration. The study focuses on critical dielectric parameters, such as dielectric constant (εr), quality factor (Qf values), and temperature coefficient (τfvalues), measured at microwave frequencies. The unique findings of this research highlight the importance of calcination temperatures in determining the ceramics’ phase purity, grain size, and density, thereby influencing their dielectric properties. These original findings, not previously reported, identify optimal calcination temperatures for both Ca0.61La0.26TiO3 and Ca0.61Nd0.26TiO3, with each material exhibiting distinct temperature dependencies due to the different ionic radii and chemical properties of La3+ and Nd3+. These original results significantly enhance our understanding of how calcination temperature affects microwave dielectric performance, offering essential guidance for developing high-performance dielectric materials for advanced communication technologies.
Keywords: Calcination temperature, Microwave, Dielectric properties, Dielectric materials.
Microwave dielectric materials, which are crucial to modern communication technologies such as satellite communications, mobile phones, and GPS systems, must exhibit specific dielectric properties, such as a high dielectric constant (εr), low dielectric loss (high-quality factor, Qf ), and a stable temperature coefficient of resonant frequency (τf) [1-7]. Among various ceramic materials, calcium titanate-based ceramics, particularly Ca0.61M0.26TiO3 (M=La3+, Nd3+), have shown promise due to their favorable dielectric properties and thermal stability [8-13]. Therefore, this research has significant practical implications for developing high-performance dielectric materials. By understanding the effect of calcination temperature on the dielectric properties of these materials, researchers and engineers can optimize the manufacturing process, leading to the production of more efficient and reliable communication technologies. This makes it a crucial study for professionals in the field.
The synthesis process of these ceramics, especially the calcination stage, is crucial in determining their final dielectric properties. Calcination, a thermal treatment process, influences the precursor powders’ phase formation, particle size, and homogeneity, subsequently affecting the microstructure and sintered ceramics’ performance [14-19]. Previous studies have shown that calcination temperature significantly impacts ceramic materials’ phase composition and densification behavior, ultimately affecting their dielectric properties. Despite the significance of calcination, there is a need for a systematic study to understand how different calcination temperatures impact the microwave dielectric properties of Ca0.61M0.26TiO3 (M=La3+, Nd3+) ceramics.
This study aims to fill this gap by investigating the effects of varying calcination conditions (temperatures and holding times) on the microwave dielectric properties of Ca0.61Nd0.26TiO3 and Ca0.61La0.26TiO3. By examining these effects, the research seeks to optimize the calcination conditions to achieve superior dielectric performance. Understanding these relationships will provide valuable insights for the fabrication of high-performance microwave dielectric materials, contributing to advancements in communication technology.
To investigate the impact of calcination temperature on the microwave dielectric properties of Ca0.61M0.26TiO3 (M=La3+, Nd3+) ceramics, the following experimental procedure was employed:
Material Preparation
High-purity raw materials, such as CaCO3, TiO2, La2O3, and Nd2O3, were used as the initial powders. These powders were measured according to the stoichiometric ratio of Ca0.61M0.26TiO3 (where M represents La3+ or Nd3+). They were then combined and thoroughly homogenized using a planetary ball mill with agate balls for 24 hours, utilizing distilled water as the milling medium.
Calcination
The homogenized powder mixtures were first dried and then calcined. This process was carried out at different temperatures, specifically 1100 °C and 1200 °C, with withholding times ranging from 1 to 6 hours in the air, to investigate the impact of temperature. Following calcination, the powders were ground to break up any agglomerates that had formed during the thermal treatment.
Sintering
The calcined powders were compressed into cylindrical pellets utilizing a uniaxial press at a pressure of 200 MPa. These pellets underwent sintering in air at temperatures ranging from 1350 °C to 1450 °C for durations spanning 1 to 5 hours. These sintering conditions were established through prior experimentation to achieve optimal densification.
Characterization
X-ray diffraction (XRD) was employed to analyze the phase composition of both the calcined and sintered samples, ensuring phase purity and detecting any secondary phases. Additionally, scanning electron microscopy (SEM) was utilized to investigate the microstructure and particle size of the sintered samples. The bulk density of these sintered samples was determined through the Archimedes method.
Microwave Dielectric Property Measurements
The dielectric constant (εr) and quality factor (Qf) were determined using a network analyzer operating within microwave frequency ranges. For the assessment of the temperature coefficient of resonant frequency (τf), measurements were conducted by tracking the resonant frequency over a temperature range spanning from 25 °C to 85 °C [20, 21].
Data Analysis
The influence of calcination temperature on dielectric properties was investigated by contrasting the εr, Qf, and τf values of samples subjected to varying calcination temperatures and durations. These findings were then correlated with the samples' phase composition, microstructure, and density to pinpoint the optimal calcination temperature for each composition Ca0.61M0.26TiO3 (M=La3+, Nd3+).
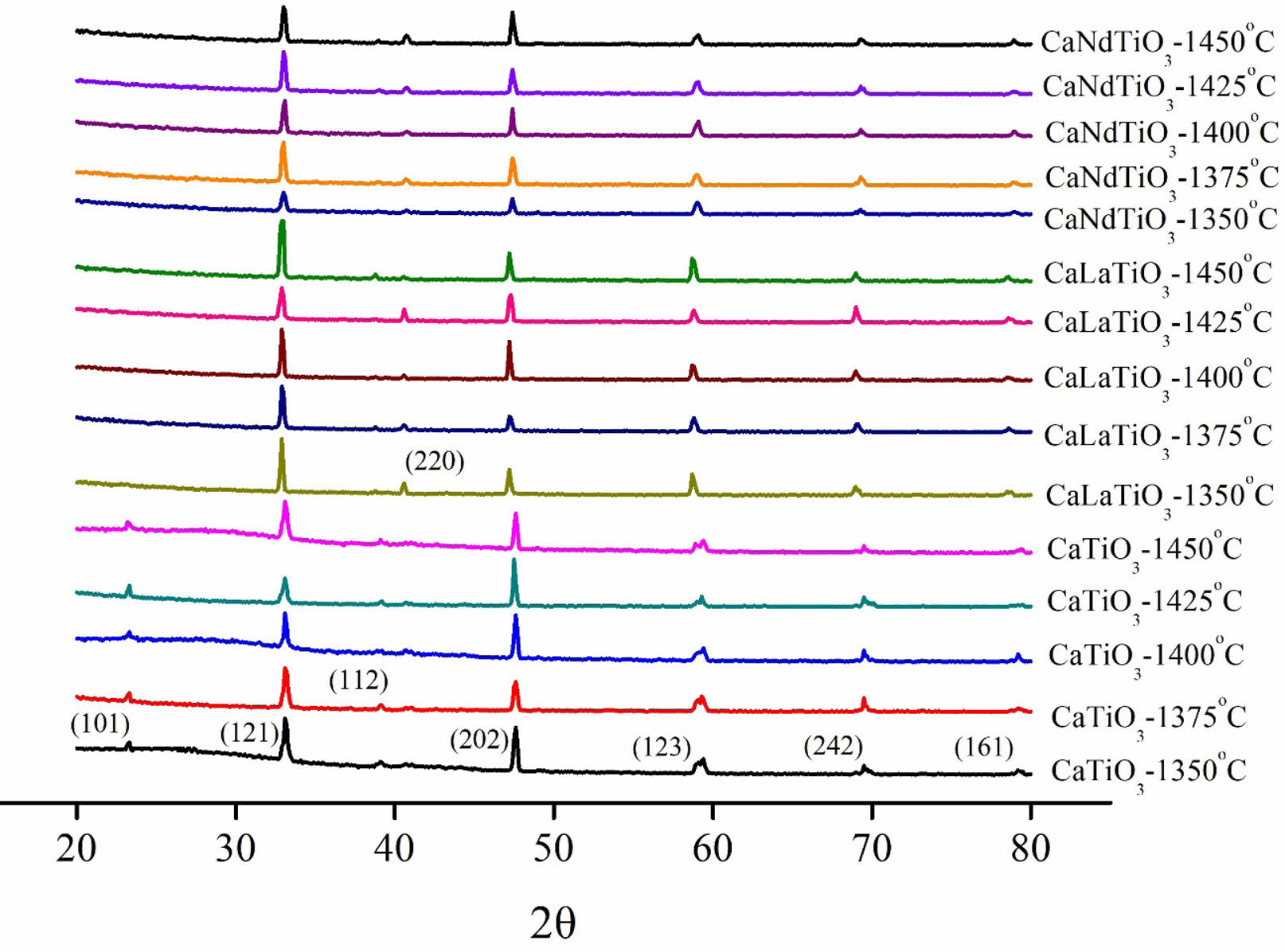
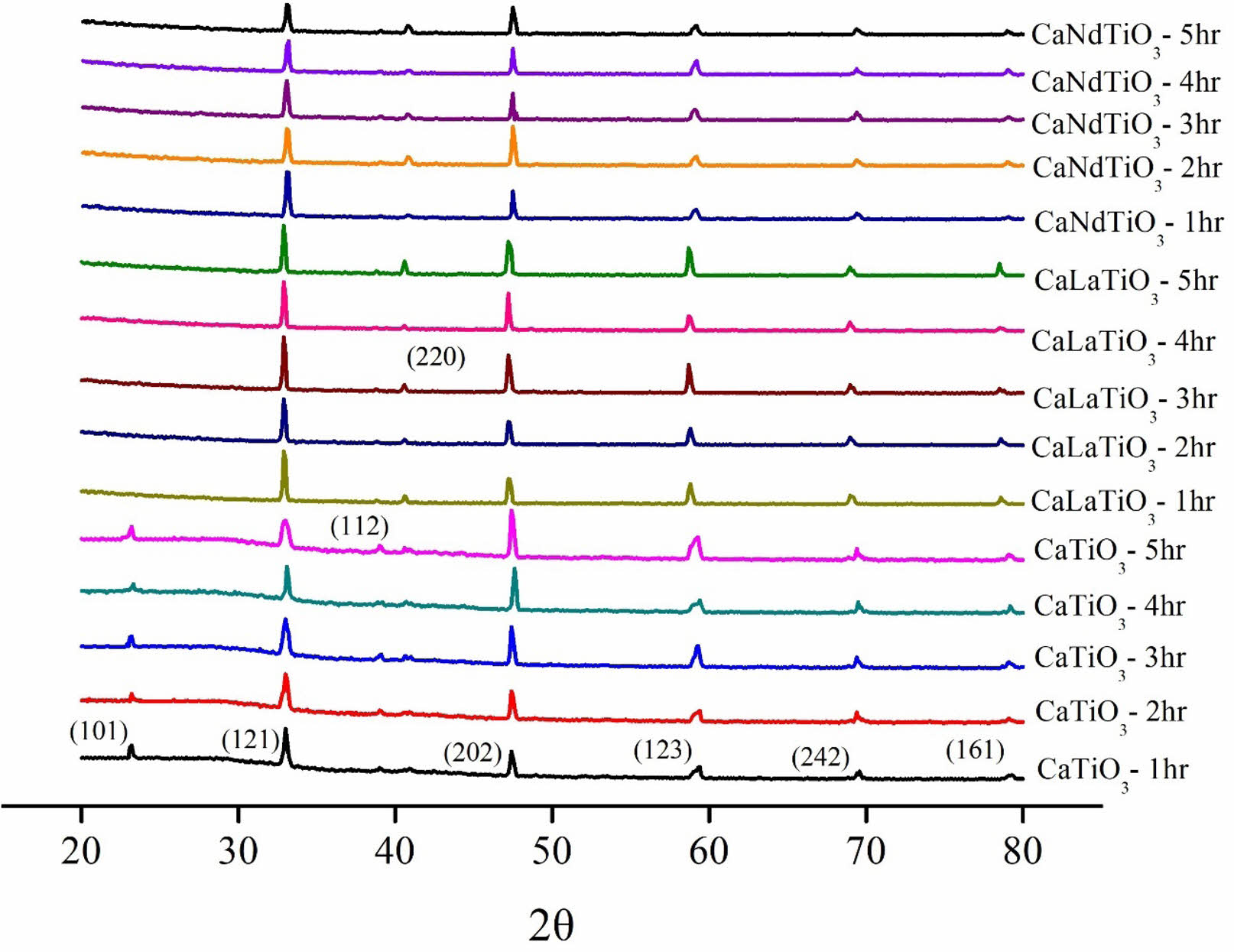
X-ray diffraction (XRD) analysis was conducted to examine the phase composition and crystallographic structure of Ca0.61M0.26TiO3 (M=La3+, Nd3+) ceramics calcined at various temperatures and holding times are shown in Table 1. Upon comparing with JCPDS (42-0423), we confirmed that all samples are perovskite compositions. We compared the four most substantial peaks and proceeded with the experimental step. The calcination conditions chosen are 1200 °C for 3 hours for Ca0.61La0.26TiO3 and 1200 °C for 1 hour for Ca0.61Nd0.26TiO3. Fig. 1 displays the XRD diffraction patterns of Ca0.61M0.26TiO3 (M=La3+, Nd3+) ceramics sintered at different temperatures (1350 °C to 1450 °C) for 4 hours. Fig. 2 shows the diffraction patterns of these ceramics sintered at their optimal temperatures for varying holding times. As depicted in the figure, all results exhibit a single perovskite structure, indicating that changes in calcination temperature have minimal effect on the composition of the crystalline phase.
Table 1 illustrates the lattice constants of Ca0.61M0.26TiO3 (M=La3+, Nd3+) ceramics after sintering for 4 hours at different temperatures, and Table 2 displays the lattice constants of Ca0.61M0.26TiO3 (M=La3+, Nd3+) ceramics sintered at 1400 °C for varying holding times. Typically, the effects of elemental substitution on the lattice constant encompass considerations such as ionic radius, valence, crystal structure, and other relevant factors. Based on the findings, the lattice constant remains relatively unchanged after substituting La3+ and Nd3+. This indicates that the ionic radii of La3+ (1.22 Å) and Nd3+ (1.15 Å) may not differ significantly from that of Ca2+ (1.06 Å) and that the chemical formula has attained a valence equilibrium. Additionally, the XRD analysis confirms the continued presence of the perovskite structure of CaTiO3, indicating no observable alteration resulting from the substitution of La3+ and Nd3+.
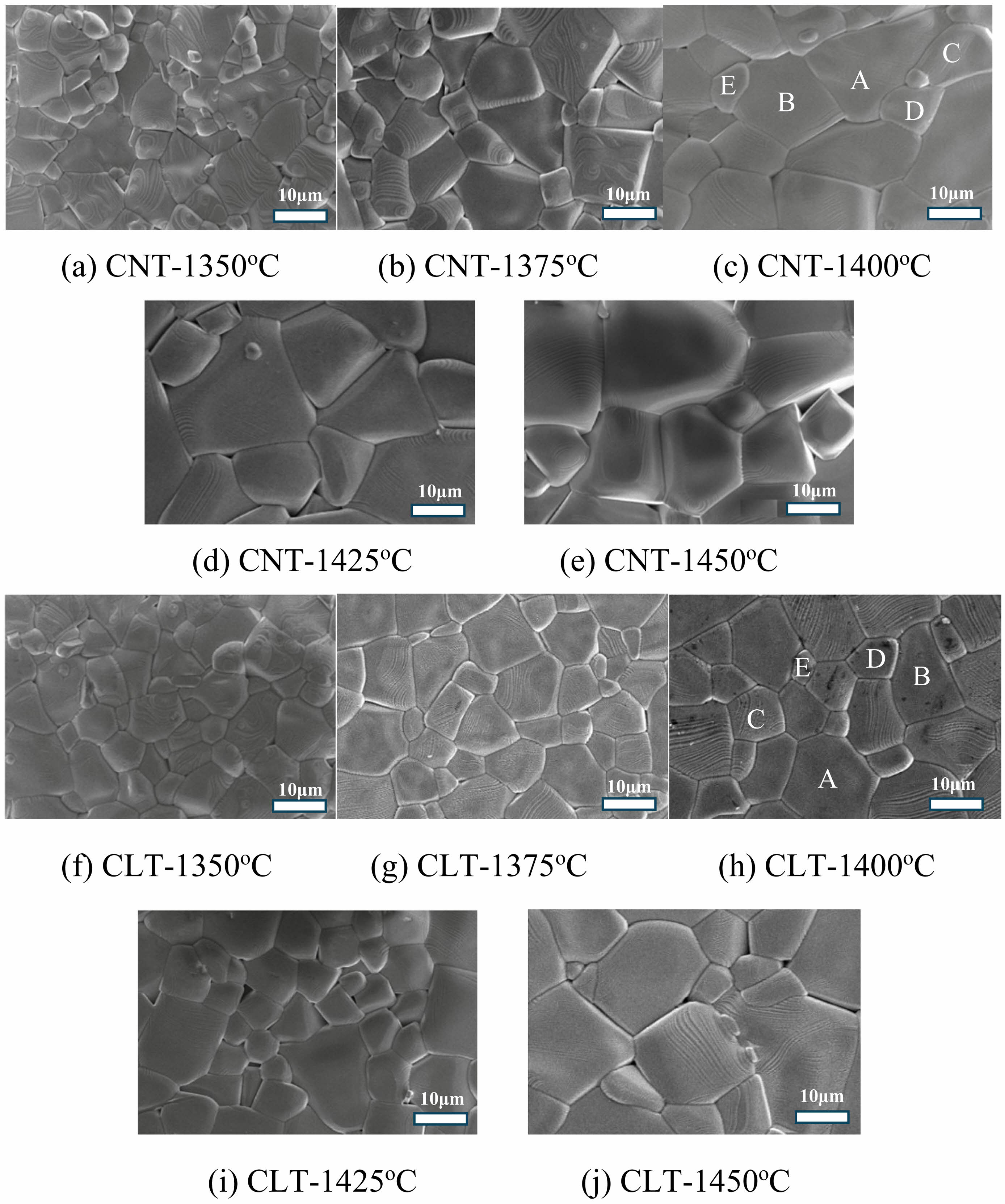
The utilization of scanning electron microscopy (SEM) offers valuable insights into the microstructural characteristics of Ca0.61M0.26TiO3 (M=La3+, Nd3+) ceramics are shown in Fig. 3 (for CaTiO3) and Fig. 4 (Ca0.61La0.26TiO3 and Ca0.61Nd0.26TiO3). The particle size variation with sintering temperature can be observed through SEM analysis of Ca0.61M0.26TiO3 (M=La3+, Nd3+) ceramics. Generally, at lower sintering temperatures, as shown in Fig. 3(a), Fig. 4(a), and (f), the particles tend to be smaller and more dispersed due to insufficient energy for grain growth and consolidation. As the sintering temperature increases, as shown in Fig. 3(c), Fig. 4(c), and (h), the energy available for atomic diffusion and grain boundary migration also increases, promoting particle growth. An optimal balance between particle growth and densification is achieved at intermediate sintering temperatures, resulting in well-defined grain boundaries and a uniform particle size distribution. This is often associated with enhanced mechanical properties and improved electrical conductivity. However, at excessively high sintering temperatures, as shown in Fig. 3(e), Fig. 4(e), and (j), particle coarsening may occur, leading to the formation of large particles and possible grain boundary discontinuities. This can adversely affect the material’s properties by increasing its susceptibility to mechanical failure and reducing its electrical performance [22-26]. In summary, SEM analysis of Ca0.61M0.26TiO3 (M=La3+, Nd3+) ceramics reveals that particle size tends to increase with sintering temperature up to an optimum, beyond which further increases may lead to detrimental effects on microstructural homogeneity and material properties. Comparable outcomes may arise concerning the holding time at a particular temperature, shown in Fig. 3(f)-(i), wherein particle size augmentation is observable until an optimal threshold is reached. Beyond this point, a continued increase in particle size could detrimentally impact microstructural consistency and material characteristics. Table 3
The Energy Dispersive X-ray Spectroscopy (EDS) analysis results provide valuable information regarding the elemental composition of Ca0.61M0.26TiO3 (M=La3+, Nd3+) ceramics are shown in Table 4. The EDS analysis reveals the elemental composition of the ceramic, including the concentrations of calcium (Ca), titanium (Ti), and the substituent elements La and Nd. The EDS findings indicate that, regardless of their visual characteristics, the grains predominantly consist of Ca0.61M0.26TiO3 (M=La3+, Nd3+), a conclusion that aligns with the XRD analysis results discussed earlier.
The relationship between density and dielectric constant (εr) with sintering temperature can be elucidated through experimental observations of Ca0.61M0.26TiO3 (M=La3+, Nd3+) ceramics are shown in Fig. 5. Generally, as the sintering temperature increases, the density of the ceramics tends to rise due to enhanced particle rearrangement and densification processes. This increase in density is often accompanied by a corresponding improvement in the dielectric constant (εr) of the ceramics, as a denser microstructure allows for more efficient polarization of the material under an applied electric field. At lower sintering temperatures, where densification is incomplete, the ceramics may exhibit lower densities and dielectric constants (εr) due to voids, pores, and incomplete particle bonding. As the sintering temperature is raised to an optimal range, densification becomes more complete, resulting in higher densities and improved dielectric properties. However, over-sintering may occur at excessively high sintering temperatures, leading to grain coarsening and the formation of voids or defects. This can result in a decrease in density and, consequently, a reduction in the dielectric constants (εr) of the ceramics. Additionally, excessive grain growth may disrupt the uniformity of the microstructure, leading to variations in dielectric properties across the material. In summary, the density and dielectric constant (εr) of Ca0.61M0.26TiO3 (M=La3+, Nd3+) ceramics generally increase with sintering temperature up to an optimal range, beyond which further increases may lead to diminishing returns or even deterioration in material properties due to over-sintering effects.
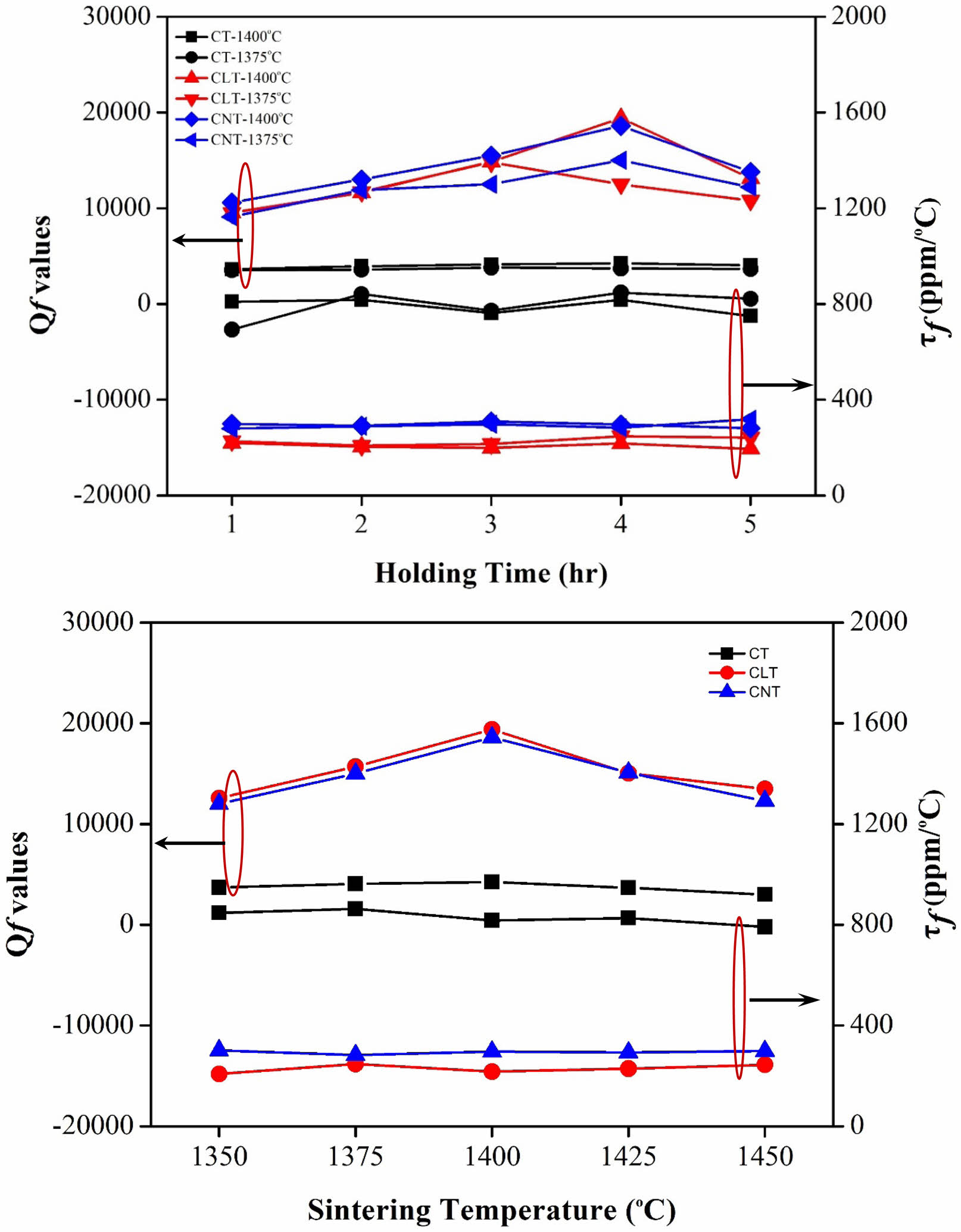
The variation of quality factor (Qf values) with sintering temperature can be observed through experimental measurements of Ca0.61M0.26TiO3 (M=La3+, Nd3+) ceramics are illustrated in Fig. 6. The quality factor, often denoted as Q, measures the energy losses in a resonant system, such as a capacitor or an inductor, relative to the stored energy. Typically, the Qf values of ceramics exhibit a non-linear relationship with sintering temperature. At lower sintering temperatures, where densification is incomplete, the material may contain defects, voids, or grain boundaries that contribute to energy losses and reduce the Qf values [27-30]. As the sintering temperature increases, densification improves, resulting in fewer defects and a more homogeneous microstructure. This can lead to a gradual increase in the Qf values of the ceramics. However, over-sintering may occur at excessively high sintering temperatures, causing grain coarsening and forming defects or grain boundary phases that can degrade the material’s performance. This can decrease the Qf values as energy losses increase due to the presence of these detrimental features. In summary, the Qf values of Ca0.61M0.26TiO3 ceramics typically increase with sintering temperature as densification improves, followed by a possible decline at excessively high temperatures due to over-sintering effects. When sintering at 1400 °C/4 h, the highest Qf value is 19,400 (GHz) for Ca0.61La0.26TiO3, 18,600 (GHz) for Ca0.61Nd0.26TiO3. Optimizing the sintering temperature is crucial to achieving the highest quality factor and maximizing the performance of the ceramic material in various applications.
The temperature coefficient (τf values) primarily investigates the susceptibility of materials' dielectric properties to ambient temperature changes. Generally, the τf values are predominantly influenced by the composition and presence of secondary phases within the material mixture. As can be seen from Fig. 6, the τf values do not change with the sintering temperature or holding times.
In summary, modifying the calcination conditions has improved the dielectric properties of Ca0.61M0.26TiO3 (M=La3+, Nd3+) ceramics. The corresponding dielectric properties are summarized in Table 5. To delve deeper into the enhancing use temperature characteristics, we blended Ca0.61La0.26TiO3 and MgTiO3 to mitigate the temperature-related variations. The corresponding dielectric properties are detailed in Table 6. The data from Table 6 illustrates that incorporating Ca0.61La0.26TiO3 enhances the temperature characteristics of MgTiO3. This implies that by appropriately adjusting the content of Ca0.61La0.26TiO3, the material composition can achieve superior temperature stability. Overall, the refinement of temperature characteristics in dielectric materials is vital for ensuring electronic components' reliability and optimal performance across varying thermal environments.
|
Fig. 1 The XRD results of Ca0.61M0.26TiO3 (M=La3+, Nd3+) ceramics at different sintering temperatures. |
|
Fig. 2 The XRD results of Ca0.61M0.26TiO3 (M=La3+, Nd3+) ceramics at their optimum sintering temperatures for various holding times. |

|
Fig. 3 The SEM images of CaTiO3 ceramics were obtained with various sintering temperatures and holding times. |
|
Fig. 4 The SEM images of Ca0.61M0.26TiO3 (M=La3+, Nd3+) ceramics were obtained with various sintering temperature for 4hr. |

|
Fig. 5 The apparent density (D) and dielectric constant (εr values) of Ca0.61M0.26TiO3 (M=La3+, Nd3+) ceramics with various holding times and sintering at varied temperatures. |
|
Fig. 6 Qf and τf values of Ca0.61M0.26TiO3 (M=La3+, Nd3+) ceramics with various holding times and sintering at varied temperatures. |
|
Table 1 XRD results of Ca0.61M0.26TiO3 (M=La3+, Nd3+) ceramics at different calcine temperatures and holding times (top 4 intensities). |
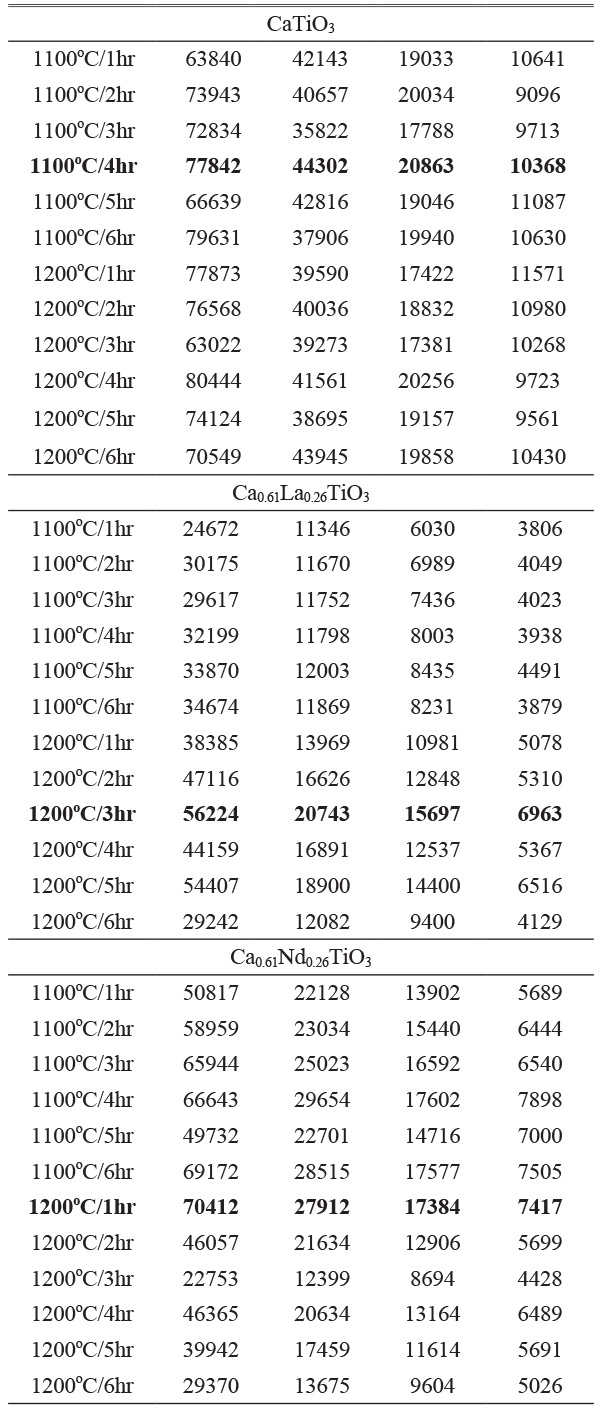
|
Table 2 The lattice parameters of Ca0.61M0.26TiO3 (M=La3+, Nd3+) ceramics sintered at varied temperatures for four h. |
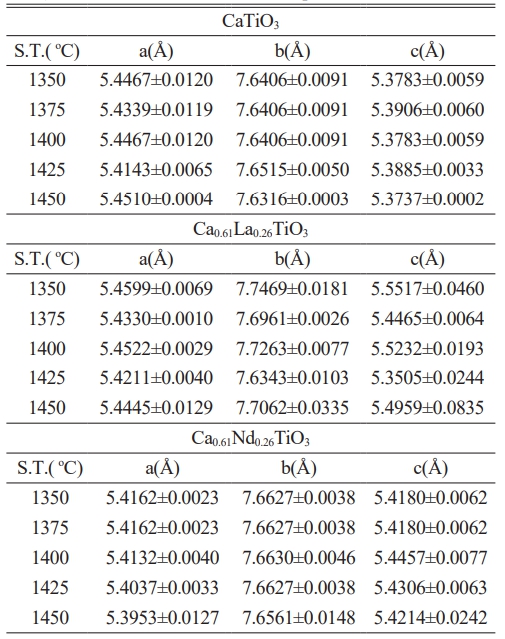
(S.T.: Sintering Temperature) |
|
Table 3 The lattice parameters of Ca0.61M0.26TiO3 (M=La3+, Nd3+) ceramics sintered at 1400 oC for varied holding times. |
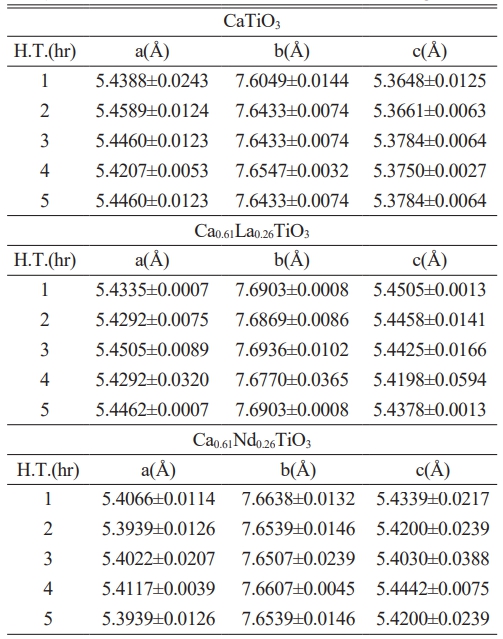
H.T.: Holding Time |
|
Table 4 The EDS results of particle formation for various spots are in Figure 3 (c), 4(c), and 4(h). |
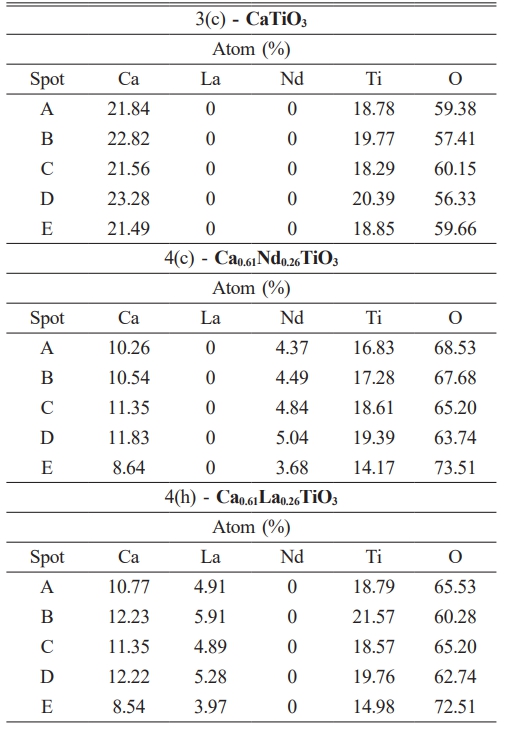
|
Table 5 The dielectric performances of Ca0.61M0.26TiO3 (M=La3+, Nd3+) ceramics with various calcine temperatures and sintering at their optimal temperature. |
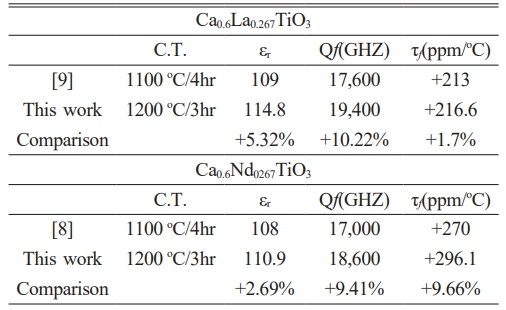
|
Table 6 The dielectric performances with various x values for (1-x) MgTiO3-xCa0.6La0.8/3TiO3 ceramics. |
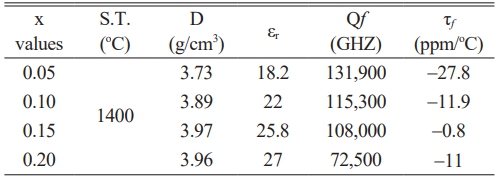
Through experimental verification, we have confirmed that modifying the calcination conditions of the material can positively influence the dielectric properties of the Ca0.61M0.26TiO3 (M=La3+, Nd3+) ceramics. Adjusting the calcination temperature increased the quality factor (Qf values) by 10% in Ca0.61La0.26TiO3 and 9% in Ca0.61Nd0.26TiO3. To evaluate the effect on temperature characteristics, we experimented with mixing Ca0.61La0.26TiO3 and MgTiO3 into a dielectric ceramic system. The results show significant improvements in temperature stability. Highly temperature-stable dielectric material composition can be achieved by appropriately adjusting the ratio of Ca0.61La0.26TiO3 to MgTiO3. When the ratio of Ca0.61La0.26TiO3 to MgTiO3 is 85:15, the dielectric characteristics obtained are a dielectric constant (εr) of 25.8, a Qf value of 108,000 (GHz), and a temperature coefficient (τf) of -0.8 (ppm/°C).
- 1. P.C. Chen, C.L. Pan, K.C. Lin, and C.H. Shen, J. Ceram. Process. Res. 25[2] (2024) 278-284.
-

- 2. Y.S. Park and E.S. Kim, J. Ceram. Process. Res. 23[6] (2022) 920-926.
-

- 3. S. Kim, J. Ceram. Process. Res. 18[6] (2017) 421-424.
-

- 4. M.C. Paul, A. Dhar, S. Das, M. Pal, S.K. Bhadra, A.M. Markom, N.S. Rosli, A. Hamzah, H. Ahmad, and S.W. Harun, IEEE Photonics J. 7[5] (2015).
-

- 5. Y. Jang, J. Kim, S. Kim, and K. Lee, IEEE Microw. Wirel. Common. Lett. 24 (2014) 665-667.
-

- 6. K. Wakino, K. Minal, and H. Tamura, J. Am. Ceram. Soc. 67[4] (1984) 278-281.
-

- 7. S. Nomura, K. Toyama, and K. Kaneta, Jpn. J. Appl. Phys. 21 (1982) L624-L626.
-

- 8. M. Yoshida, N. Hara, T. Takada, and A. Seki, Jpn. J. Appl. Phys. 36 (1997) 6818-6823.
-

- 9. C.L. Huang, J.T. Tasi, and Y.B. Chen, Mater. Res. Bull. 36[3-4] (2001) 547-556.
-

- 10. C.L. Huang, C.F. Tasi, and Y.B. Chen, J. Alloy Comp. 453[1-2] (2008) 337-340.
-

- 11. C.L. Huang, Y.B. Chen, and C.F. Tasi, J. Alloy Comp. 454[1-2] (2008) 454-459.
-

- 12. V. M. Ferreira, F. Azough, J.L. Baptista, and R. Freer, J. Mater. Res. 12[12] (1992) 3293-3299.
-

- 13. I.S. Kim, W.H. Jung, Y. Inaguma, and T. Nakamura, Mater. Res. Bull. 30[3] (1995) 307-316.
-

- 14. X. Kuang, G. Carotenuto, and L. Nicolais, Adv. Perform. Mater. 4 (1997) 257-274.
-

- 15. N. Saikumari, S. Monish Dev, and S. Avinaash Dev, Sci. Rep. 11 (2021) 1734-1751.
-

- 16. Y. Fang, A. Hu, S. Ouyang, and J.J. Oh, J. Eur. Ceram. Soc. 21 (2001) 2745-2750.
-

- 17. Y.F. Chen, C.Y. Lee, M.Y. Yeng, and H.T. Chiu, J. Cryst. Growth 247 (2003) 363-370.
-

- 18. Y.J. Choi, J.H. Park, J.H. Park, S. Nahm, and J.G. Park, J. Eur. Ceram. 27[4] (2007) 2017-2024.
-

- 19. T. Bongkarn and C. Wattanawikkam, Ferroelectrics 382 (2009) 42-48.
-

- 20. B.W. Hakki and P.D. Coleman, IRE Trans. Microwave Theory Tech. 8 (1960) 402-410.
-

- 21. W.E. Courtney, IEEE Trans. Microwave Theory Tech. 18 (1970) 476-485.
-

- 22. C.H. Shen and C.L. Pan, Int. J. Appl. Ceram. Technol. 12 (2015) E127-E133.
-

- 23. C.L. Huang and J.Y. Chen, J. Alloy. Compd. 485 (2009) 706-710.
-

- 24. C.L. Huang, S.S. Liu, and S.H. Chen, Jpn. J. Appl. Phys. 48 (2009) 071402-071404.
-

- 25. C.L. Huang and S.S. Liu, J. Alloy. Compd. 471 (2009) L9-L12.
-

- 26. C.L. Huang, J.J. Wang, and Y.P. Chang, J. Am. Ceram. Soc. 90 (2007) 858-862.
-

- 27. B.D. Silverman, Phys. Rev. 125 (1962) 1921-1928.
-

- 28. G.L. Gurevich and A.K. Tagantsev, Sov. Phys. JETP. 64 (1986) 142-151.
- 29. V.L. Gurevich and A.K. Tagantsev, Adv. Phys. 40 (1991) 719-767.
-

- 30. D. Kajfezz and P. Guillon, “Dielectric Resonators,” (Noble Publishing Corporation, Atlanta, US 1998).
 This Article
This Article
-
2024; 25(5): 790-797
Published on Oct 31, 2024
- 10.36410/jcpr.2024.25.5.790
- Received on Jun 14, 2024
- Revised on Jul 17, 2024
- Accepted on Jul 31, 2024
 Services
Services
Shared
 Correspondence to
Correspondence to
- Chun-Hsu Shen
-
Department of Electronic Engineering, Ming Chuan University, 5 De Ming Rd., Gui Shan District, Taoyuan City 333, Taiwan
Tel : +886 3 350-7001 ext. 3737 Fax: +886 3 359-3877 - E-mail: chshen0656@mail.mcu.edu.tw






 Copyright 2019 International Orgranization for Ceramic Processing. All rights reserved.
Copyright 2019 International Orgranization for Ceramic Processing. All rights reserved.