- Color-tunable nanopigments of ZnSxSe1−x: Preparation, optical properties, and first-principles evaluation
Ti Zhangb,c, Yanmin Wanga,*, Shanjun Keb,c,* and Zhidong Pana
aSouth China University of Technology, Guangzhou 510640, China
bFoshan Oceano Ceramics Co. Ltd., Foshan 528138, China
cGuangxi Oceano Ceramics Co. Ltd., Wuzhou 543300, ChinaThis article is an open access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
In this work, the effects of the crystalline structure and charge state distribution on the bandgap, dominant wavelength, and optical properties of ZnSxSe1−x color-tunable nanopigments were investigated for the first time. The first-principles calculation results of ZnSxSe1−x pigment based on density functional theory demonstrate that ZnSxSe1−x becomes a material with an adjustable optical bandgap due to the similarity of S and Se. Furthermore, the ZnSxSe1−x pigment color gradually changed from ivory white to bright yellow with increasing anion composition of x = [S]/([S] + [Se]), thereby obtaining tunable colors and optical properties to meet visual and aesthetic requirements.
Keywords: ZnSxSe1−x, Optical properties, Kubelka-Munk theory, First-principles evaluation.
Recently, inorganic nanopigments [1-5] with tunable colors [6, 7], aesthetic features [8], and nontoxic elements [9, 10] have become important candidates for thermal reflection cold materials in reducing the energy consumption of buildings [11-13]. Inorganic pigments can obtain different colors through selective absorption and reflection in the visible light region [14, 15]. The rational design of pigment compositions produces diversified colors to develop tunable colorful pigments [16].
With high solar/near-infrared (NIR) reflectance, low cost and color-turntable properties, ZnSxSe1−x has been paid much attention as a novel cool pigments. It can be applied to the complex inorganic color pigments (CICP), ceramic tiles, cool coatings and many others fields. The optical properties of ZnS/ZnSe systems are closely related with their band structure [17-20]. The bandgap of ZnSxSe1−x is affected by phase structure and the component ratios (x). The bandgap width and the energy levels between the conduction band and the valence band will have an affect on the color-turntable properties of the ZnSxSe1−x systems.
In this paper, we have aimed at exploring the Kubelka–Munk optical properties and band structure of ZnSxSe1−x pigments with a controllable crystalline structure and optical properties. The effects of the crystalline structure and charge state distribution on the bandgap, dominant wavelength, and optical properties of ZnSxSe1−x pigments were initially explored.
Synthesis
ZnSxSe1−x pigments (x = 1, 0.75, 0.55, and 0.35) were synthesized by acoprecipitation reaction and subsequent calcination (Fig. A1) using ZnSO4·7H2O (99.5%), Na2S·9H2O (98%), and Se (99%), NaOH (97%) as starting materials supplied by Sinopharm Group Co. Ltd., China. The value of x changes for compositions of ZnSxSe1−x precursors (see Table A1).
Theoretical method
The CASTEP package was employed to calculate the band structure of ZnSxSe1−x using first-principle calculations based on density functional theory (DFT). The geometric structure optimization of ZnS0.35Se0.65 was first performed by Perdew–Burke–Eruzerh (PBE) in the generalized gradient approximation (GGA) scheme to exchange–correlation effects, and ultrasoft pseudopotentials were used for electron interactions. In addition, the calculation functional used is PBE. A plane-wave cutoff energy of 460 eV was employed in the calculations, which assured a total energy convergence of 2.0 × 10−6 eV/atom. In order to build ZnS0.35Se0.65 crystals, the ZnS crystal was initially built as a basic model [21]. ZnS0.35Se0.65 was set up using GGA by changing the composition of S atoms by substituting 65% virtual Se atoms. The Brillouin zone (BZ) was set with the 6 × 6 × 6 Monkhorst–Pack k–point meshes (Fig. A2). Zn 3d104s2, S 3s23p4, and Se 4s24p4 were considered the valence states, respectively, and the electrons of the remaining orbitals are described by frozen-core approximation.
Characterizations
The crystalline phases of samples were examined on an X-ray diffractometer (PW-1710, Netherlands). The Fourier transform infrared spectra of samples were recorded on a Fourier infrared spectrometer (VERTEX 33, USA) in a frequency range of 400–4000 cm−1. Moreover, X-ray photoelectron spectroscopy (ESCALAB 250Xi, USA) and ultraviolet–visible–near-infrared (UV–vis–NIR) spectrophotometer (LAMBDA 950, USA) were used to determine the element valence state and diffuse reflectance of samples, respectively, using BaSO4 as a reference.
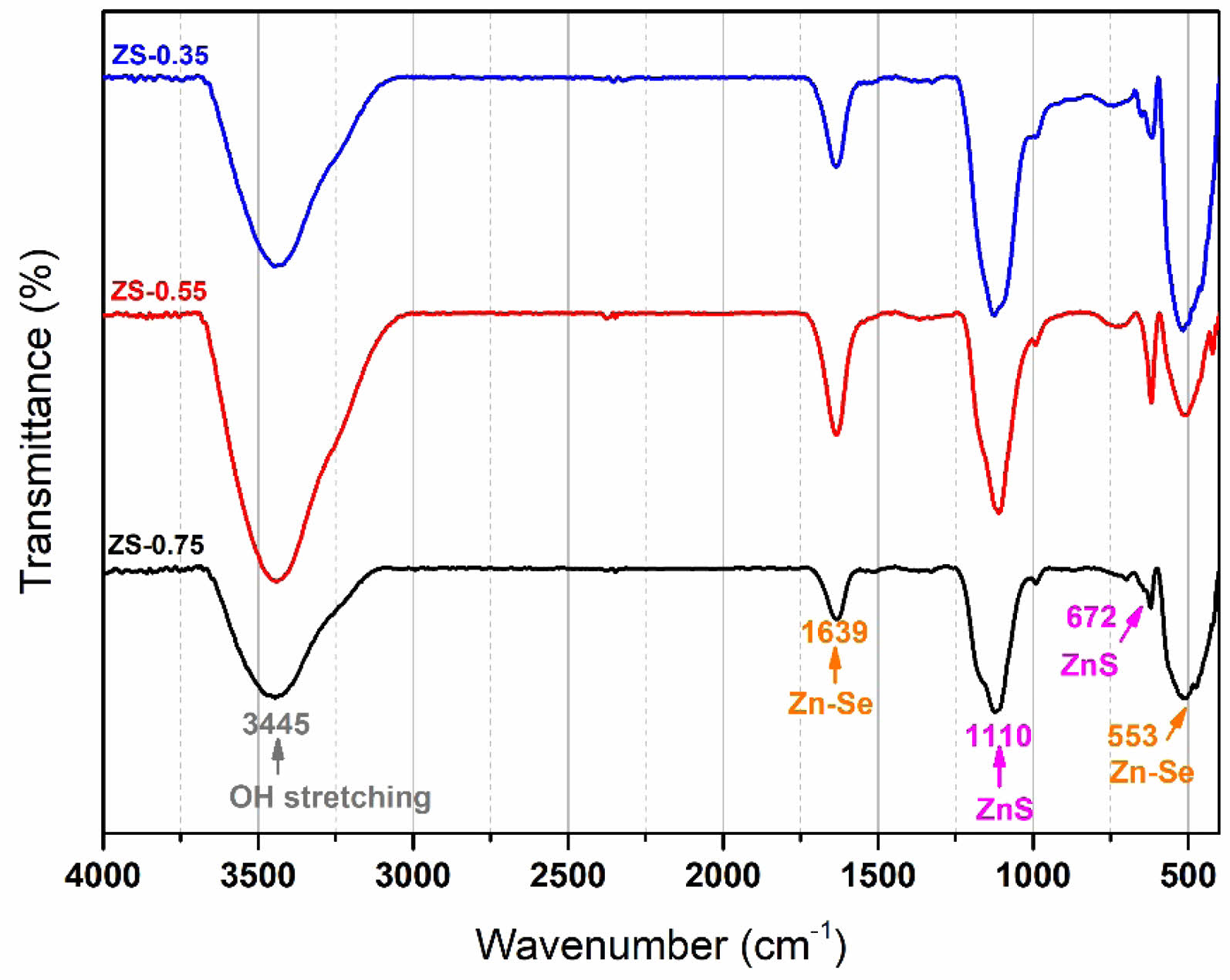
|
Fig. 1 Fourier-transform infrared spectra of ZnSxSe1−x
pigments. |
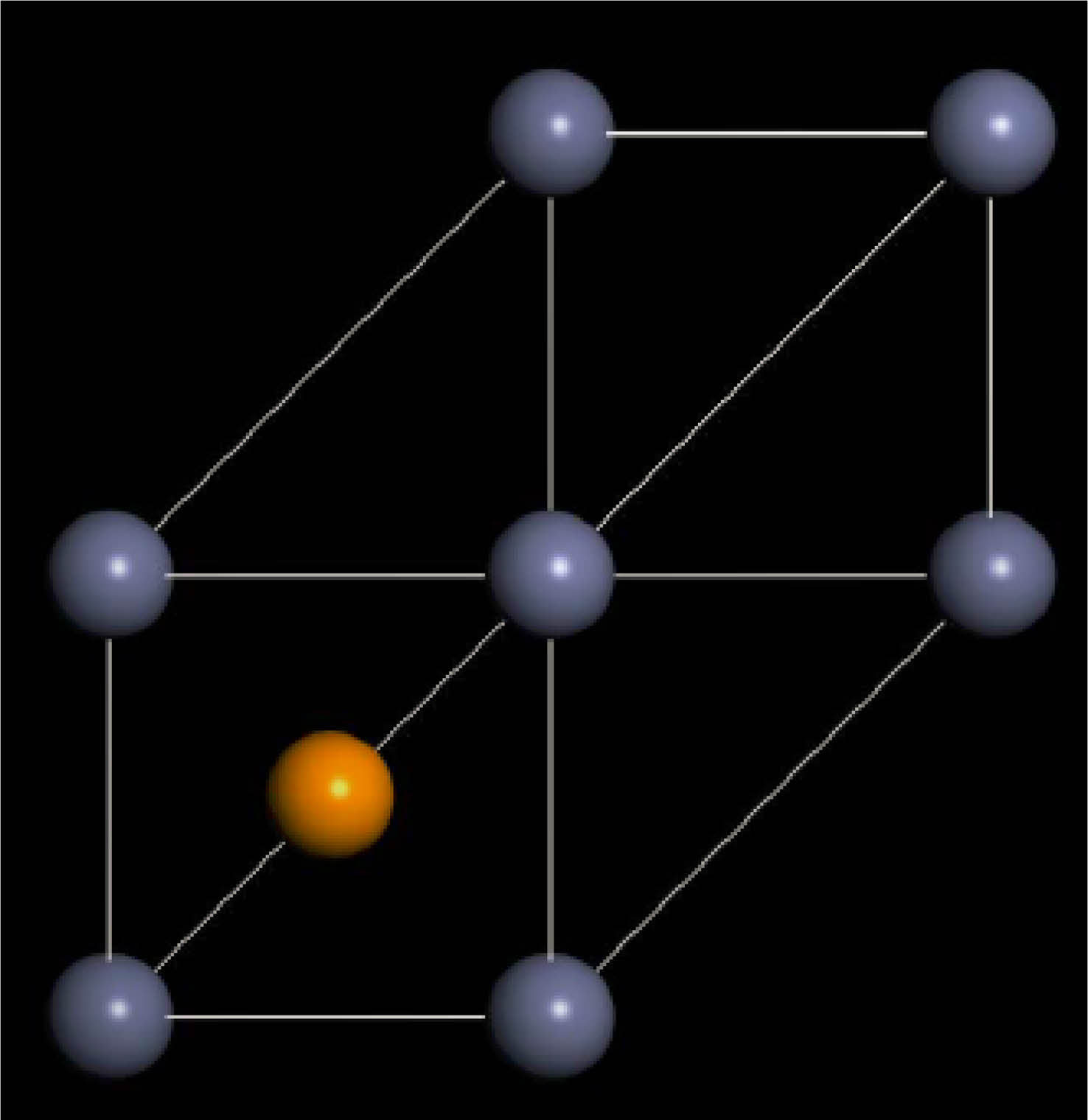
|
Fig. 2 Cell structure of ZnS0.35Se0.65 calculated on the basis of first principles. |
Crystalline structure analysis
Fig. 1 presents the Fourier-transform infrared (FTIR) spectra of ZnSxSe1−x pigments after annealing at 600℃. The FTIR spectra have sharp peaks at 1110 and 672 cm−1, assigned to the vibration of Zn–S and Zn–Se bonds (see Table 1), respectively. It was confirmed that a ZnSxSe1−x solid solution was formed in the samples.
Fig. A2 shows the X-ray diffraction patterns of ZnSxSe1−x(x = 1, 0.75, 0.55, and 0.35) pigments after annealing at 600℃. The possible reaction equation is as follows:
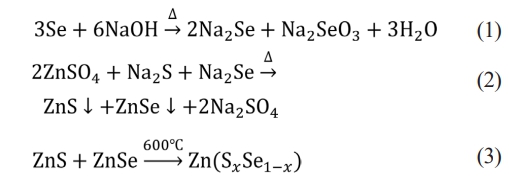
With an increase in Se content in ZnSxSe1−x, the (111) and (220) crystal planes of ZnSxSe1−x move in the direction of lower 2θ values, and the lattice parameters also increase (see Table 2).
First-principles study
The ideal zinc blende structure of ZnS and ZnSe belong to the cubic crystal system, F-43 m (no. 216) lattice group. The unit cell structure model following first-principles calculations is shown in Fig. 2, where the composition of S atoms in ZnS varies by substituting 65% virtual Se atoms. Furthermore, the unit cell parameter a of ZnS0.35Se0.65 is 5.497 Å, and the unit cell volume is 166.10 Å. The error between the unit cell parameter a and experimental test value (ZS-0.35, a = 5.6672 Å, Table 1) is 3.0%, which is within the allowable error range (±5%).
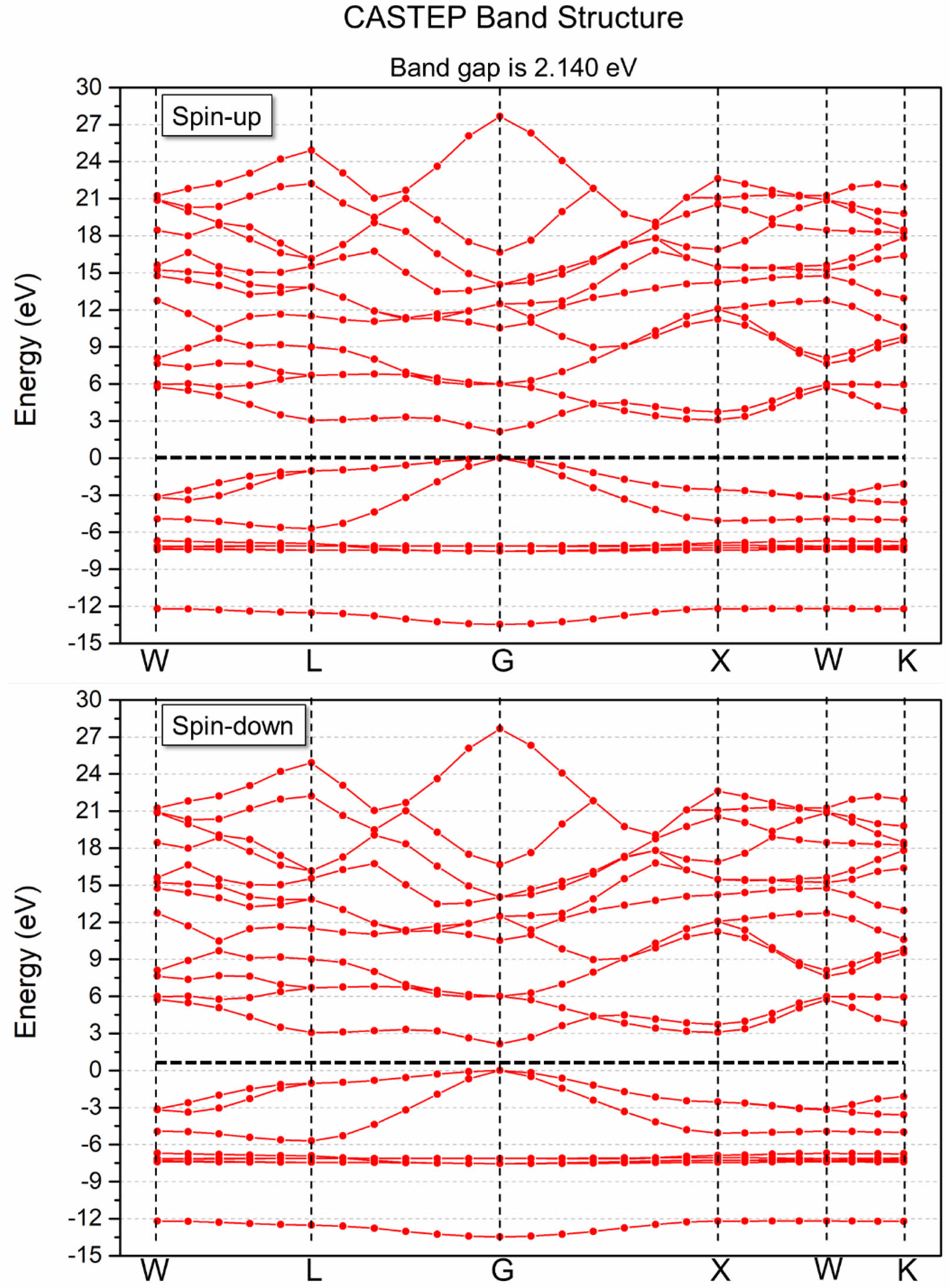
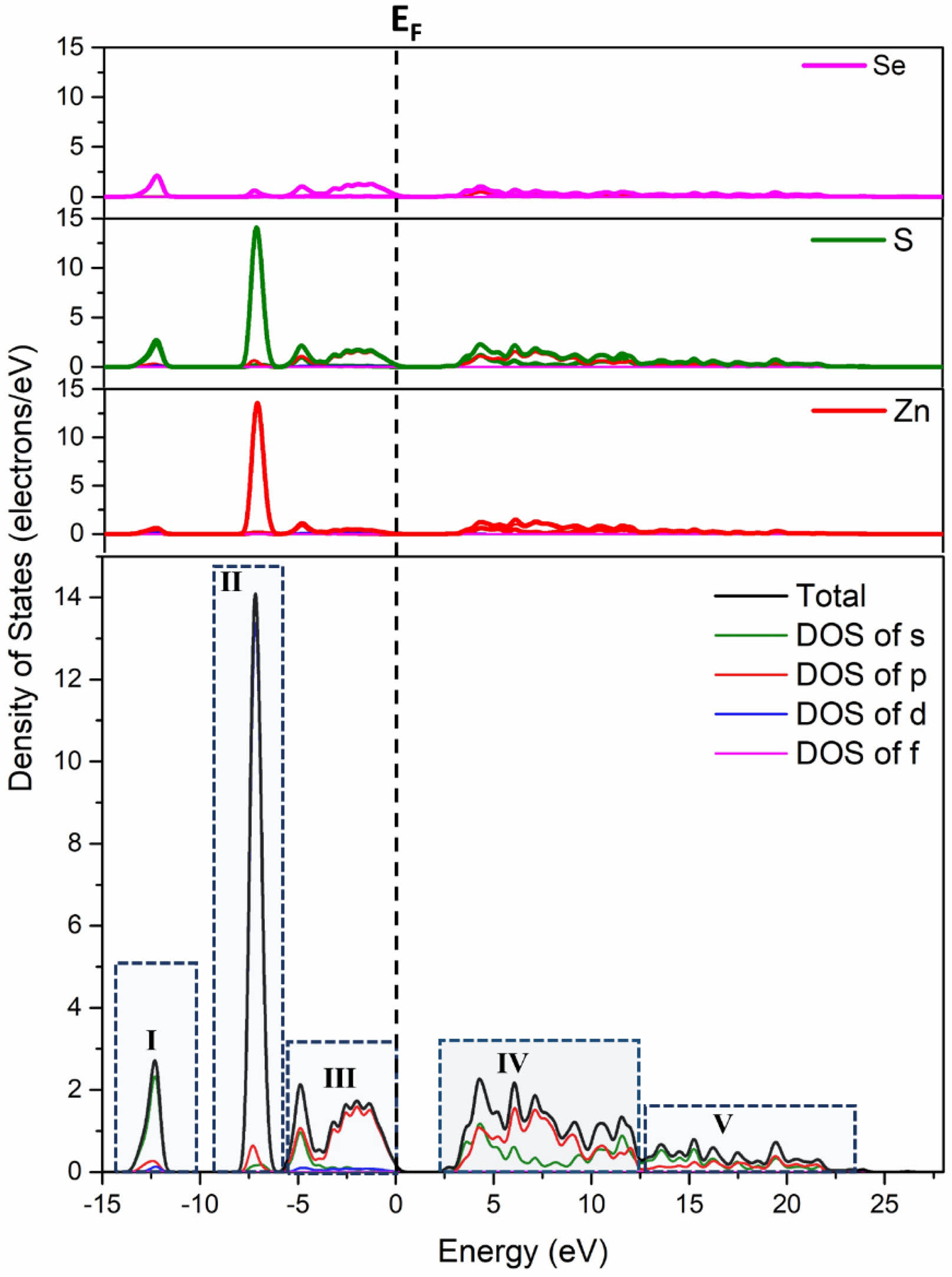
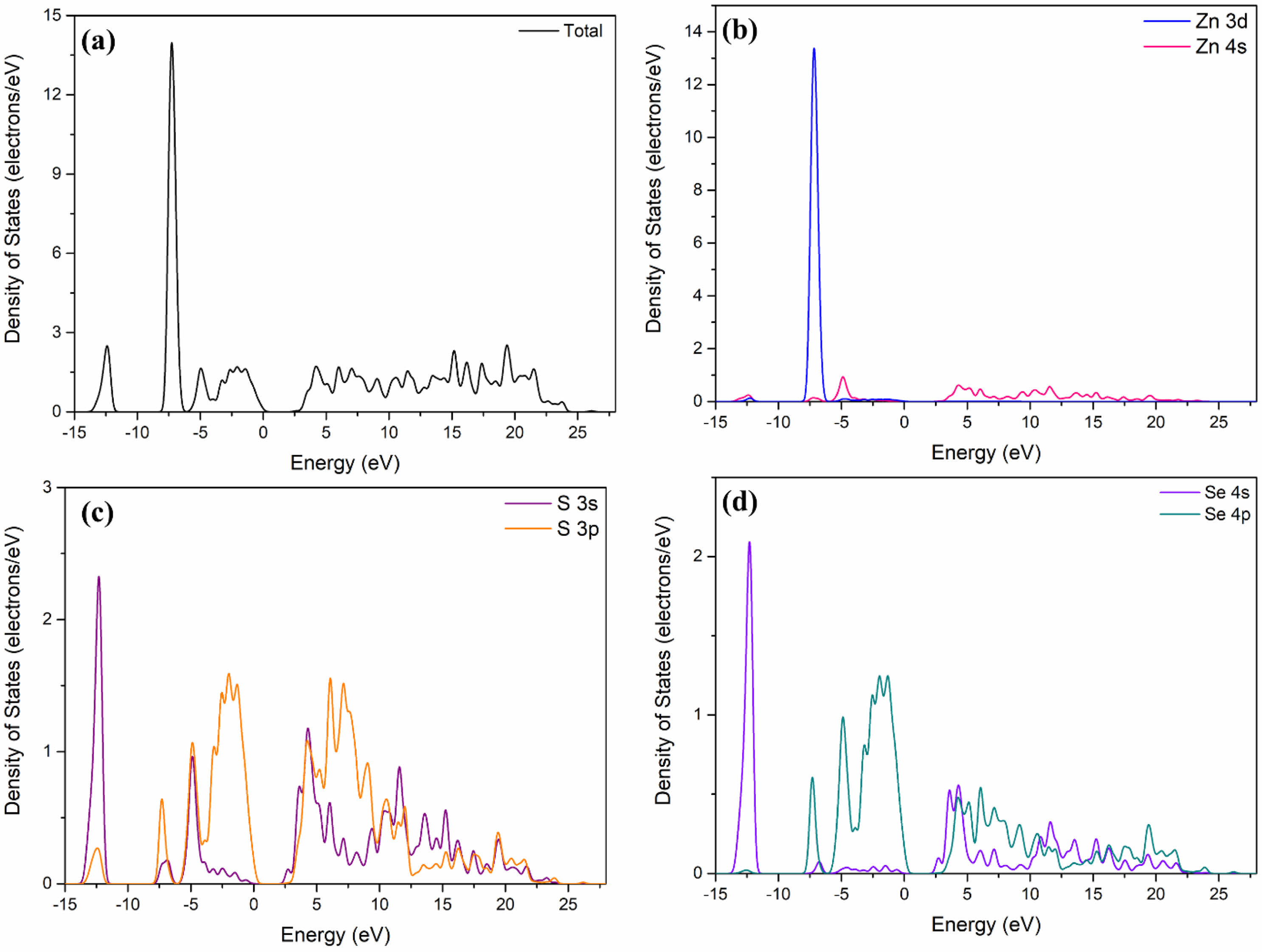
The calculated band structure of ZnS0.35Se0.65 based on the first principles is shown in Fig. 3. The bottom and top of the conduction and valence bands of ZnS0.35Se0.65, respectively, are located at point G in the BZ after setting the Fermi level EF = 0 eV. Moreover, ZnS0.35Se0.65 has an indirect electronic transition type, signifying that ZnSxSe1−x is a direct bandgap semiconductor material with a tunable optical bandgap [25]. The calculated bandgap value of ZnS0.35Se0.65 is 2.140 eV, which is lower [26] than the experimental test value (ZS-0.35, Eg = 2.68 eV, Table 3). The total state density distribution of ZnS0.35Se0.65 and partial state density distribution of Zn, S, and Se were calculated to determine the electronic contribution near the Fermi level (Fig. 4 and Fig. 5).
For ZnSe, the valence band region of -3–0 eV is composed of Se 4p states, while the conduction band of 2–4 eV is mainly composed of the hybridization of Zn 4s and Se 4p states. The existence of electrons in the Zn 4s state in the conduction band indicates that the charge is transferred from Zn to Se; the presence of electrons in the Se 4p state in the conduction band signifies that the charge transfer is incomplete. Similar to the structure of ZnSe, the valence band near the Fermi level of ZnS0.35Se0.65 mainly comes from the p state of S/Se.
Due to the similarity of S and Se, the first-principles calculation results of ZnSxSe1−x pigment based on DFT establish that ZnSxSe1−x becomes a material with an adjustable optical bandgap. The color of the ZnSxSe1−x pigment can be varied by changing the component value x, and tunable color and optical properties can be obtained (Fig. 6).
Kubelka–Munk optical properties
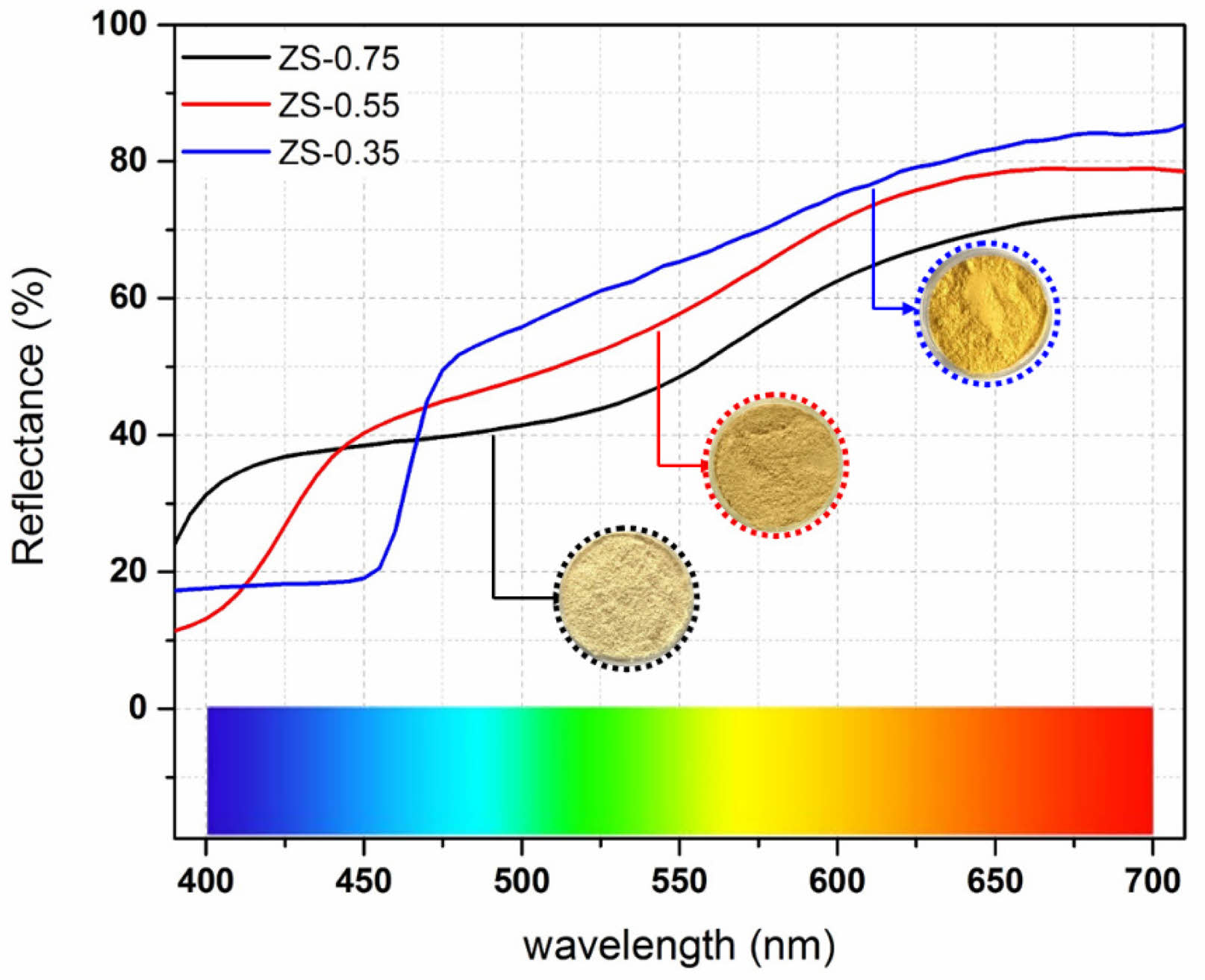
Fig. 6 displays the UV–vis diffuse reflectance spectra of ZnSxSe1−x pigments. The pigment reflectance in the UV–vis region rose varying degrees with increasing Se content in the ZnSxSe1−x pigments, so their color gradually changed from ivory white to bright yellow.
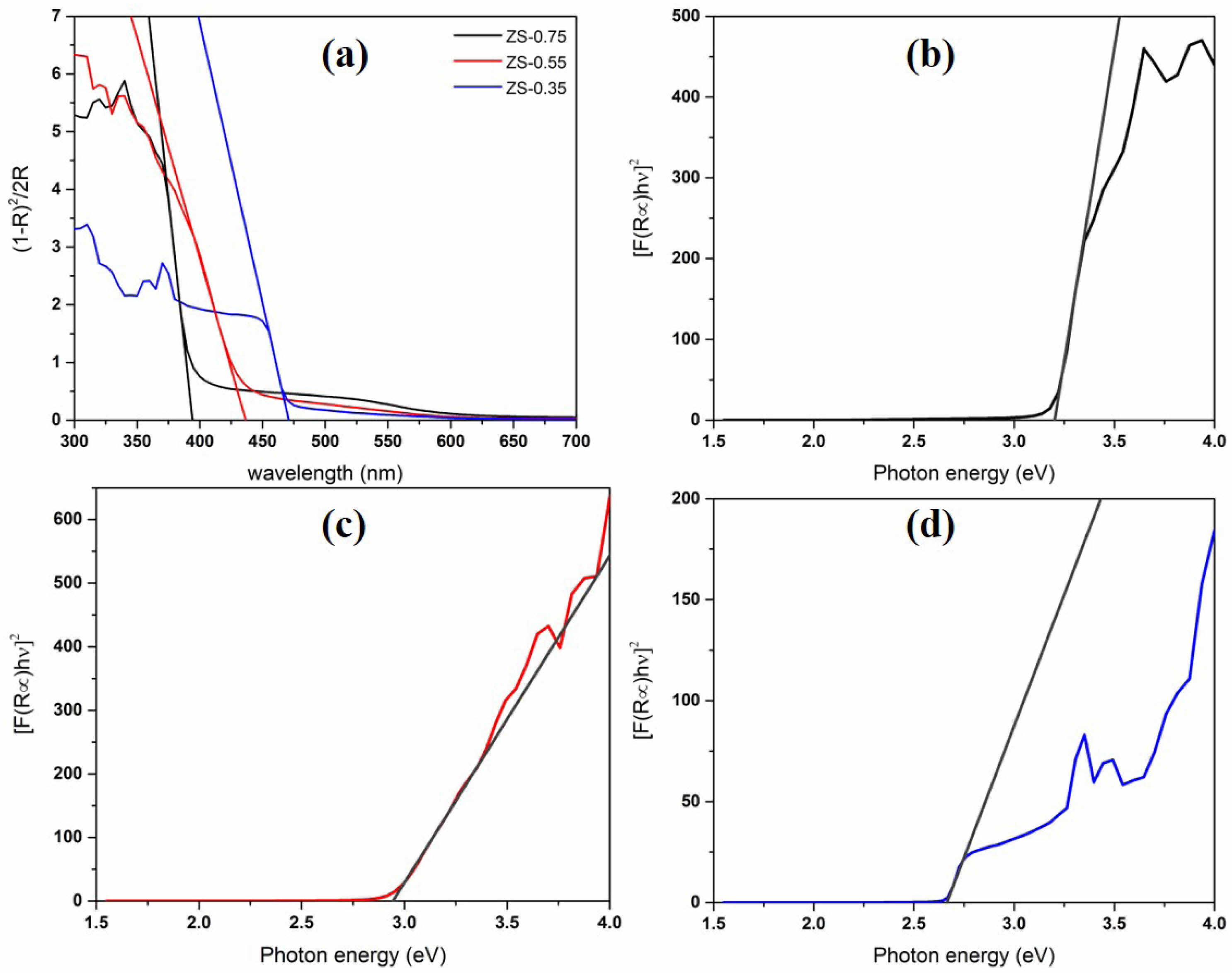
The Kubelka–Munk (K–M) model is used to describe the optical behavior of pigments in the visible light region. According to the K–M theory [27], the K–M transformed reflectance spectra are drawn from the UV–vis diffuse reflection spectra of ZnSxSe1−x pigments (Fig. 7).
The optical absorption edge of ZnSxSe1−x pigments shifts significantly from 394 ± 0.02 nm to a longer wavelength (i.e., 472 ± 0.03 nm) with rising Se content, representing that the sample can effectively reflect the yellow hue [Fig. 7 (a)]. With the changing of the anion composition x = [S]/([S] + [Se]), the continuous movement of the optical absorption edge further confirms the formation of ZnSxSe1−x solid solution in the pigment samples.
The calculated bandgap value and absorption wavelength of ZnSxSe1−x pigments are listed in Table 3. The Eg values of ZS-0.75, ZS-0.55, and ZS-0.35 samples are 3.21, 2.94, and 2.68 eV, respectively (the estimated error is ±0.02 eV). The shift of the optical absorption edge in the ZnSxSe1−-x pigments and the resulting bandgap variation make the sample color gradually change from white to yellow (Fig. 6).
These results confirm that the ZnSxSe1−x pigments are materials with an adjustable optical bandgap. The color of ZnSxSe1−x pigments can be varied by changing the component value x, thereby obtaining tunable colors and optical properties to meet visual and aesthetic requirements.
Analysis of Vegard’s law for ZnSxSe1−x
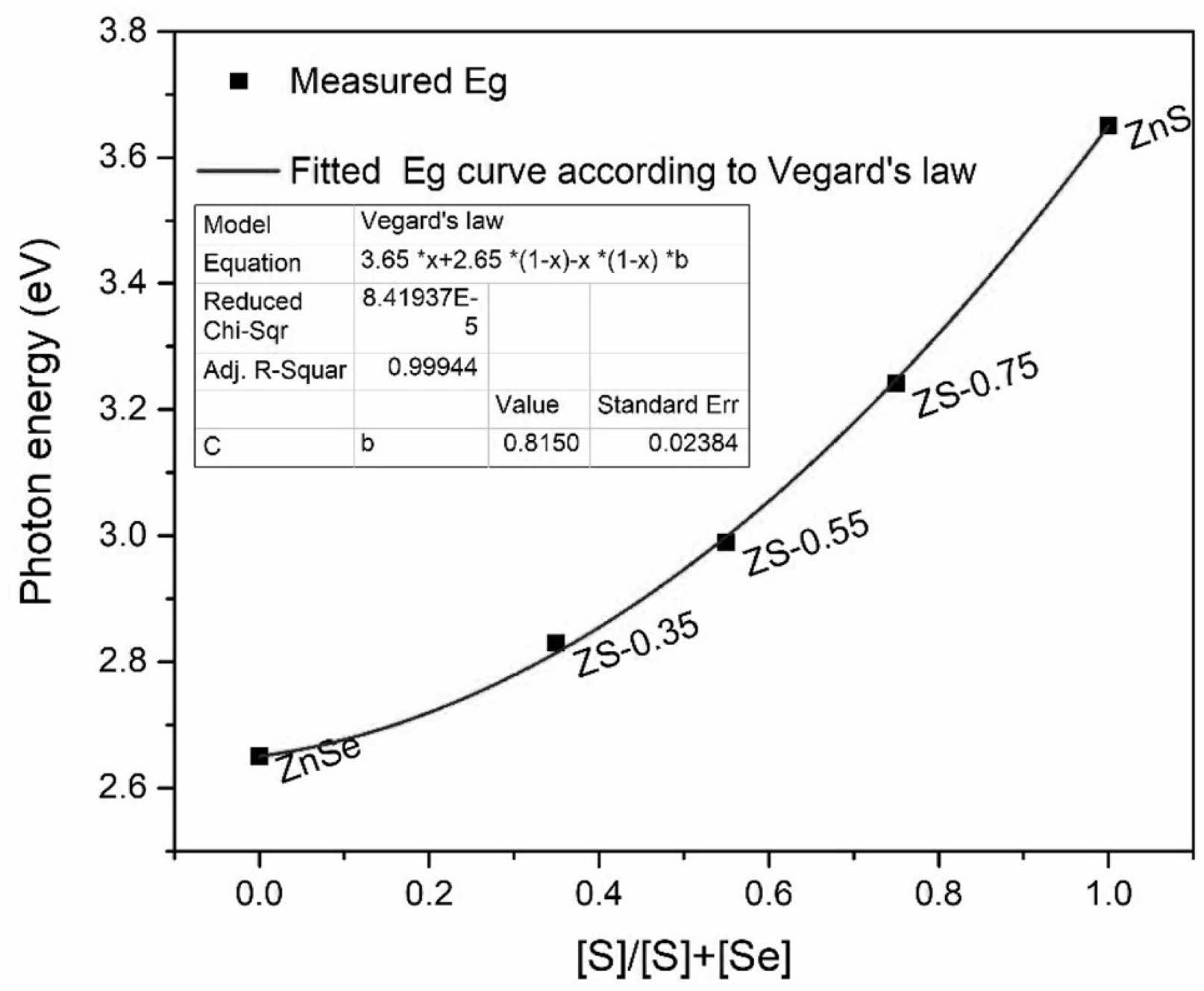
Vegard’s law [28] is used to explain the nonlinear changes in the optical bandgap and other physical properties of semiconductor alloy nanomaterials with changes in their composition. Vegard’s law shows that the lattice parameters of a ternary solid solution tend to vary linearly with the changing composition, but other physical properties, such as optical bandgap [29], usually exhibit nonlinear changes. The bandgap value of ZnSxSe1−x pigments varies with the anion composition x = [S]/([S] + [Se]), which can be fitted to the quadratic function of x,
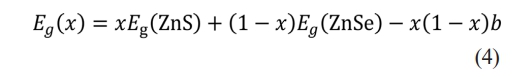
where Eg(ZnS), Eg(ZnSe), and Eg(x) are the bandgap values of ZnS, ZnSe, and ZnSxSe1−x pigments, respectively, and b is the optical bowing constant. The bending constant b describes the degree of nonlinear changes in the optical bandgap.
In the ZnSxSe1−x ternary solid solution, changing the ratio between S2− and Se2− atoms leads to the redistribution of electrons in the atom, and the variation in the negative ion bond length adapts to the ZnSxSe1−x composition of each x value [30]. Studies by Swafford et al. [30] and Ingole et al. [31] have shown that the constant b is insensitive to lattice parameters. Therefore, the optical bandgap value of the ZnSxSe1−x pigments measured in Table 3 was fitted by Origin according to Vegard’s law to obtain the value of b (Fig. 8). The dots in Fig. 8 are the experimental data, and the curve is the quadratic fitting based on the experimental results. The Origin’s best fit is b = 0.815, consistent with the results reported by Dimitrievskaet al. [21] and Chuo et al.[32].
In this study, a relatively small b value indicates that ZnSe and ZnS have excellent compatibility. Therefore, in the synthesis of ZnSxSe1−x pigments with different x component values, the predetermined optical bandgap can be adjusted by changing the molar ratio of S to Se in the raw materials so that the ZnSxSe1−x pigments can exhibit color changes (Fig. 6).
|
Fig. 3 Band structure of ZnS0.35Se0.65 based on first principles (Fermi-level EF is set to zero energy, which is represented by the horizontal black dashed lines). |
|
Fig. 4 Total state density and partial state density of ZnS0.35Se0.65 single cell (Fermi level EF is set to zero energy which is denoted by black vertical dashed lines). |
|
Fig. 5 tom state density distribution of ZnS0.35Se0.65. |
|
Fig. 6 Ultraviolet–visible diffuse reflectance spectra of ZnSxSe1−x pigments |
|
Fig. 7 Absorption edge calculated based on the Kubelka–Munk (K–M) theory (a), K–M transformed reflectance spectra (b), (c), and (d) of ZnSxSe1−x pigments. |
|
Fig. 8 Bandgap value of ZnSxSe1−x as a function of composition x (dots are the experimental data, and the curve is the quadratic fitting based on the experimental results). |
|
Table 2 Variation in lattice parameters and average crystallite size with Se concentrations. |

(1) The first-principles calculation results of ZnSxSe1−x pigment based on DFT show that ZnSxSe1−x transforms into a material with an adjustable optical bandgap due to the similarity of S and Se. The color of the ZnSxSe1−x pigment can be varied by changing the x component value, and tunable color and optical properties can be obtained.
(2) The Kubelka–Munk (K–M) model was used to describe the optical behavior of ZnSxSe1−x pigment in the visible light region. With increasing anion composition x = [S]/([S] + [Se]), the pigment lattice parameters increase, and the ZnSxSe1−x pigments’ colors gradually changed from ivory white to bright yellow. The continuous movement of the optical absorption edge further confirms the formation of ZnSxSe1−x solid solution in the pigment samples.
(3) The Analysis of Vegard’s law for ZnSxSe1−x shows that changing the ratio between S2− and Se2− atoms leads to the redistribution of electrons in the atom, and the variation in the negative ion bond length adapts to the ZnSxSe1−x composition of each x value. A relatively small optical bowing constant (b) value indicates that ZnSe and ZnS have excellent compatibility.
(4) The color of ZnSxSe1−x pigments can be varied by changing the x component value, thereby obtaining tunable colors and optical properties to meet visual and aesthetic requirements.
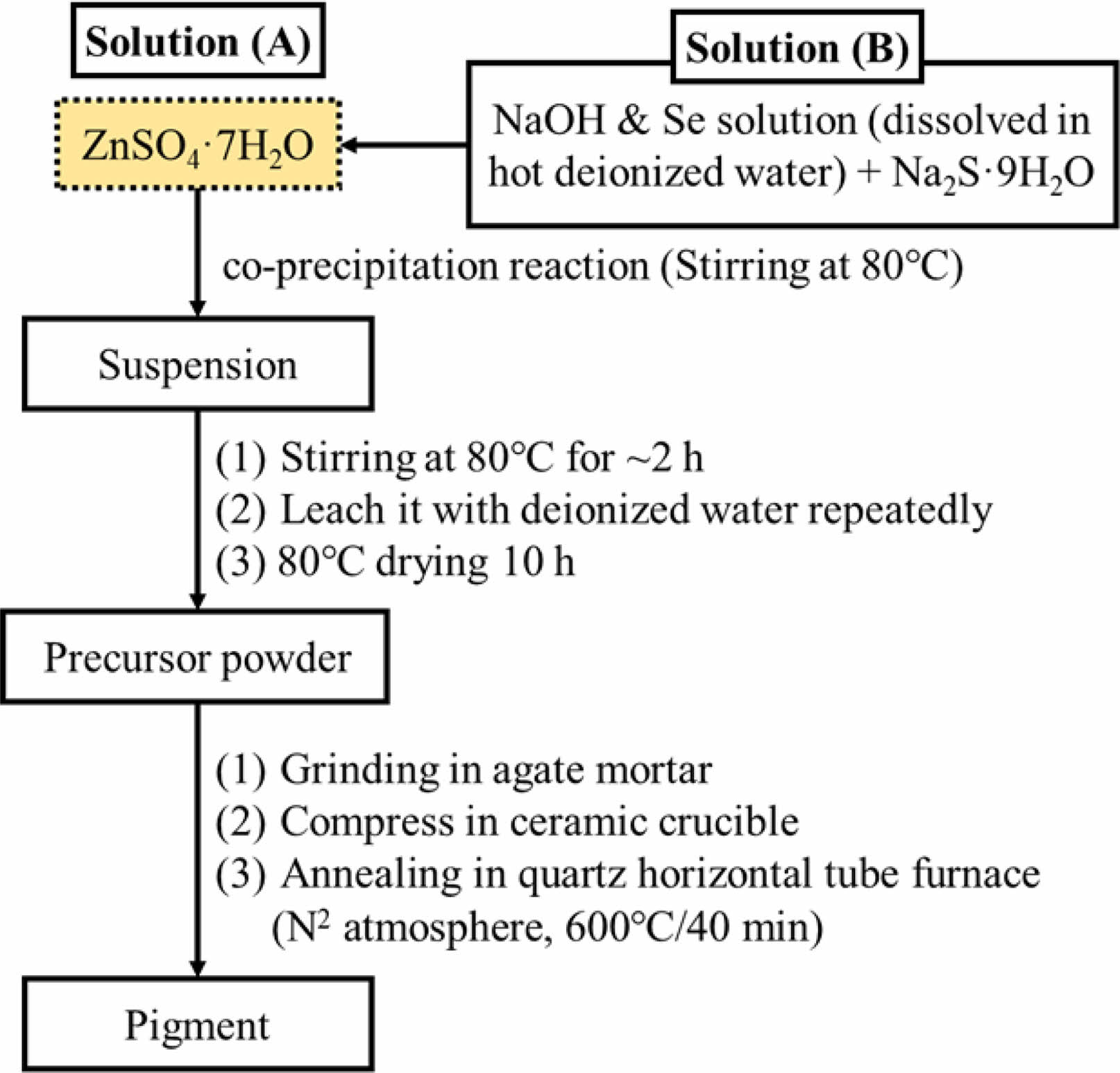
Fig. A1. Flowchart for synthesis procedure of ZnSxSe1−x pigments.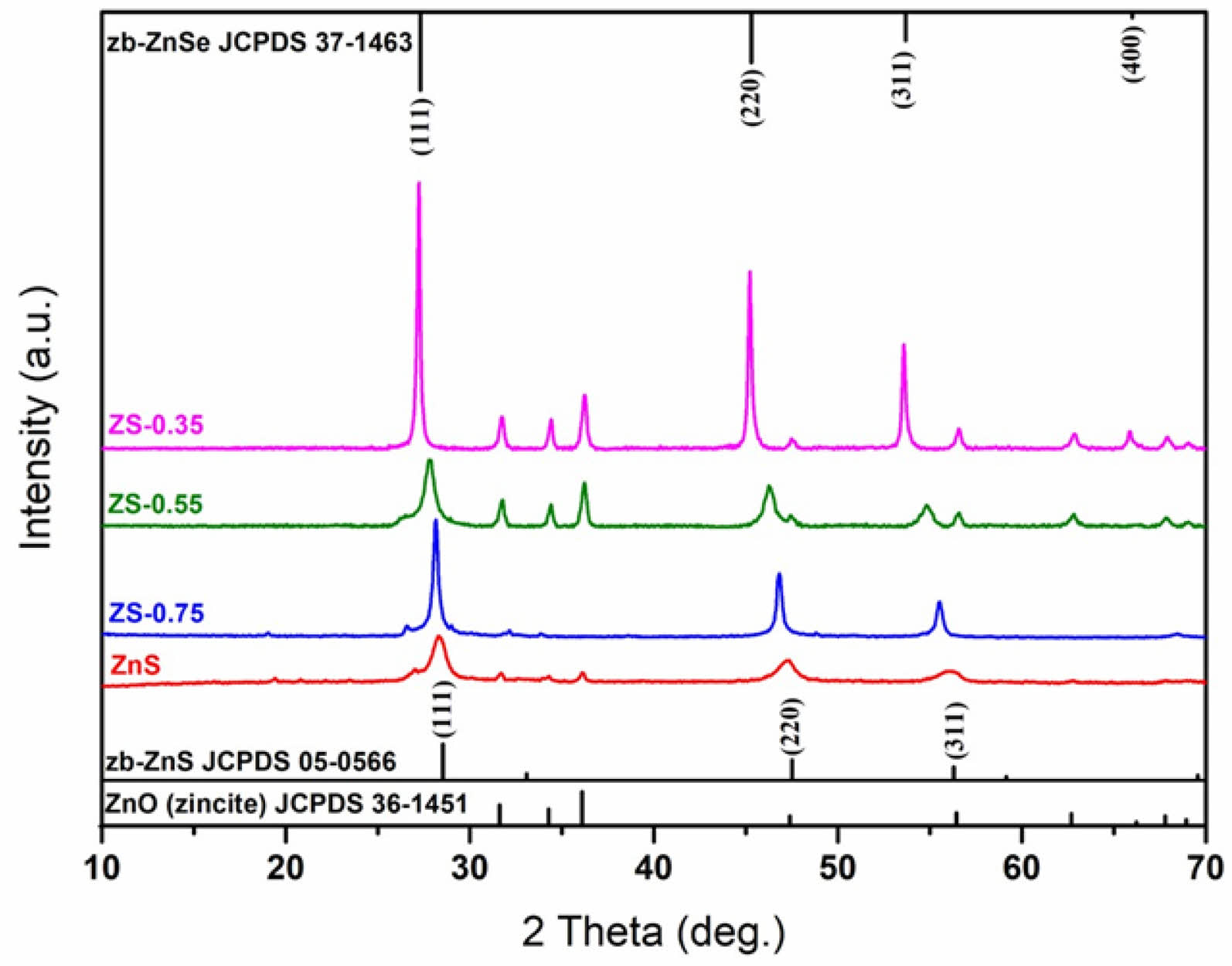
Fig. A2. X-ray diffraction patterns of ZnSxSe1−x (x = 1, 0.75,
0.55, and 0.35) pigments.
Fig. A3. Selection rules for high-symmetry points of the Brillouin
zones of ZnS0.35Se0.65 structure.
Table A1. Compositions of ZnSxSe1−x precursors.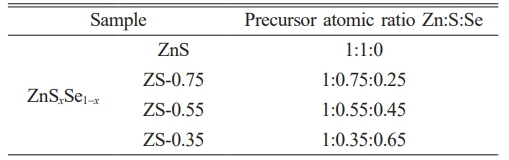
This work was supported by the Guangdong Basic and Applied Basic Research Foundation (No. 2021A1515110487) and Natural Science Foundation of Guangxi (2024GXNSFAA010520).
- 1. S. Jamshidi, S. Rasouli, B. Janipour, and B. Mirhadi, J. Ceram. Process. Res. 16 (2015) 667-673.
-

- 2. W. Chatjuthamanee, R. Muanghlua, B. Boonchom, and N. Vittayakorn, J. Ceram. Process. Res. 13 (2012) 713-716.
-

- 3. B. Tanisan and S. Turan, J. Ceram. Process. Res. 12 (2011) 462-467.
-

- 4. Y.Z. Halefoglu and E. Kusvuran, J. Ceram. Process. Res. 11 (2010) 92-95.
-

- 5. J. Zhang, Y.M. Park, X.Y. Tan, M.K. Bae, D.J. Kim, T.H. Jang, M.S. Kim, S.W. Lee, and T.G. Kim, J. Ceram. Process. Res. 20 (2019) 589-596.
-

- 6. J.H. Lee, H.J. Hwang, J.W. Kwon, J.H. Kim, K.T. Hwang, and K.S. Han, J. Ceram. Process. Res. 20 (2019) 127-132.
-

- 7. L.L. Wang, X.X. Liu, X.P. Li, X.F. Wang, L.N. Feng, and X.R. Hou, J. Ceram. Process. Res. 22 (2021) 240-245.
-

- 8. K.R. Pyon, K.S. Han, and B.H. Lee, J. Ceram. Process. Res. 12 (2011) 279-288.
-

- 9. S. Rasouli, M. Valefi, S.J. Moeen, and A.M. Arabi, J. Ceram. Process. Res. 12 (2011) 450-455.
-

- 10. S. Rasouli, J. Ceram. Process. Res. 12 (2011) 668-672.
-

- 11. M. Suwan, P. Premjit, P. Thavorniti, P. Kidkhunthod, S. Supothina, J. Ceram. Process. Res. 18 (2017) 10-15.
-

- 12. T.N. Rao, I. Hussain, Riyazuddin, and B.H. Koo, J. Ceram. Process. Res. 20 (2019) 411-417.
-

- 13. M. Ullah, H.J. Kim, J.G. Heo, D.K. Roh, and D.S. Kim, J. Ceram. Process. Res. 20 (2019) 86-91.
-

- 14. R. Azizi, S. Rasouli, N.P. Ahmadi, A.J.J. Kolaei, and M. Azizie, J. Ceram. Process. Res. 13 (2012) 164-169.
-

- 15. N. Gurbuz, E. Coskun, and E. Ozel, J. Ceram. Process. Res. 11 (2010) 184-190.
-

- 16. W. Zhou, J. Ye, Z. Liu, L. Wang, L. Chen, S. Zhuo, Y. Liu, and W. Chen, Inorg. Chem. (2021).
-

- 17. X. Tian, Z. Chen, J. Wen, Y. Du, J. Hu, S. Wang, H. Peng, J. Li, and Y. Peng, J. Ceram. Process. Res. 18 (2017) 116-121.
-

- 18. M.R. Bodke, Y. Purushotham, and B.N. Dole, J. Ceram. Process. Res. 16 (2015) 601-604.
-

- 19. K. Liu, W. Song, Y. Xu, J. Li, and Z. Wang, J. Ceram. Process. Res. 19 (2018) 146-149.
-

- 20. S.D. Yoon, J.W. Yun, and Y.H. Yun, J. Ceram. Process. Res. 21 (2020) 479-487.
-

- 21. M. Dimitrievska, H. Xie, A.J. Jackson, X. Fontane, M. Espindola-Rodriguez, E. Saucedo, A. Perez-Rodriguez, A. Walsh, and V. Izquierdo-Roca, PCCP 18 (2016) 7632-7640.
-

- 22. X.L. Guo, Q.L. Rao, L.L. Li, Y. Zou, and C. Wu, J. Ceram. Process. Res. 17 (2016) 815-817.
-

- 23. K. Petzke, Physica B 273-274 (1999) 866-869.
-

- 24. W.K. Jung, J.W. Hong, and D.H. Choi, J. Ceram. Process. Res. 22 (2021) 86-90.
-

- 25. J. Zhou and X. Wu, J. Alloys Compd. 695 (2017) 1392-1396.
-

- 26. J.P. Perdew, Int. J. Quantum Chem. 28 (1985) 497-523.
-

- 27. P. Kubelka and F. Munk, Zeitschrift fur Technische Physik 12 (1931) 593-601.
- 28. L. Vegard, Zeitschrift für Physik 5 (1921) 17-26.
-

- 29. P. Jitti-a-porn, S. Suwanboon, P. Amornpitoksuk, and O. Patarapaiboolchai, J. Ceram. Process. Res. 12 (2011) 85-89.
-

- 30. L.A. Swafford, L.A. Weigand, M.J. Bowers, J.R. McBride, J.L. Rapaport, T.L. Watt, S.K. Dixit, L.C. Feldman, and S.J. Rosenthal, J. Am. Chem. Soc. 128 (2006) 12299-12306.
-

- 31. P.P. Ingole, G.B. Markad, D. Saraf, L. Tatikondewar, O. Nene, A. Kshirsagar, and S.K. Haram, The Journal of Physical Chemistry C 117 (2013) 7376-7383.
-

- 32. H.X. Chuo, T.Y. Wang, and W.G. Zhang, J. Alloys Compd. 606 (2014) 231-235.
-

 This Article
This Article
-
2024; 25(4): 617-623
Published on Aug 31, 2024
- 10.36410/jcpr.2024.25.4.617
- Received on Mar 29, 2024
- Revised on Jul 13, 2024
- Accepted on Jul 31, 2024
 Services
Services
- Abstract
introduction
experimental
results and discussion
conclusions
appendix a.
- Acknowledgements
- References
- Full Text PDF
Shared
 Correspondence to
Correspondence to
- Yanmin Wang a, Shanjun Ke b,c
-
aSouth China University of Technology, Guangzhou 510640, China
bFoshan Oceano Ceramics Co. Ltd., Foshan 528138, China
cGuangxi Oceano Ceramics Co. Ltd., Wuzhou 543300, China
Tel : +86 20 87114883 Fax: +86 20 87110273 - E-mail: wangym@scut.edu.cn (Y. Wang), sjkescut@163.com (S.








 Copyright 2019 International Orgranization for Ceramic Processing. All rights reserved.
Copyright 2019 International Orgranization for Ceramic Processing. All rights reserved.