The present study investigated the effects of sulfuric acid doping on the structure, morphology, and sintering behavior of nano Y₂O₃ powders. The sintering kinetics of the resultant compacts during the initial sintering stage were assessed, using constant rates of heating (CRH). Compared to the undoped Y₂O₃ powder, the powder doped with sulfuric acid exhibited improved nano-scale uniformity in particle size and enhanced homogeneity in particle dispersion. The introduction of sulfuric acid as a dopant significantly boosted the densification rate of Y₂O₃ at temperatures exceeding ~1350 °C. This addition decreased the activation energy required for sintering and transformed the diffusion mechanism, shifting it from grain boundary (GB) diffusion to volume diffusion (VD) during the initial sintering stage. Microstructural and optical characterization of as-fabricated ceramics were employed to further evaluate the sintering behavior of powders. When being sintered at 1500 ℃ in vacuum, a homogeneous microstructure was observed in the ceramic derived from the doped Y₂O₃ powder, whereas large amounts of pores were presented in the undoped sample. At a sintering temperature of 1700 ℃ for 5 h, the undoped ceramic appeared opaque, while the doped sample exhibited remarkable transparency, achieving a transmittance of approximately 74% at a wavelength of 2000 nm.

Keywords: Sintering behaviour, Transparent ceramics, Y₂O₃ nano-powders, Sulfuric acid.

Yttria (Y₂O₃) transparent ceramics possess various outstanding physical, mechanical, and chemical characteristics, such as high-temperature stability, robust corrosion resistance, and excellent optical transparency. These exceptional qualities of Y₂O₃ transparent ceramics have led to their extensive development and employment in various optical applications, including missile infrared domes, semiconductor components, host materials for scintillators, as well as solid lasers, etc. [1-4].
In order to achieve superior transparency in sintered materials, internal porosity must be eliminated entirely in the final sintering stage [5, 6]. More recent works have been focused on the utilization of nanopowders with high sintering activity [2], as well as various sintering techniques such as hot pressing (HP) [7], hot isostatic pressing (HIP) [8], spark plasma sintering (SPS) [9, 10], or their combinations [11]. Furthermore, doping with sintering additives containing HfO₂ [12], La₂O₃ [13], ThO₂ [14], LiF [15], and ZrO₂ [16] has been investigated as a potential method to enhance the transparency of ceramics. Fu et al. [17] obtained transparent Y₂O₃ by a combination of air presintering at 1500 ℃ and HIP sintering at 1550 ℃ under 200 MPa pressure, using ZrO₂ as sintering additives. ZrO₂ suppressed grain boundary mobility while promoted pore pinning, causing highly dense ceramics. The in-line transmittance at 1100 nm (1.0 mm thick) wavelength reached 81.4%. Although pressure-assisted sintering methods are effective for producing highly transparent ceramics, these methods have substantial limitations, particularly when producing components with large sizes and complex geometrical shapes. Additionally, the high-pressure operating environment also poses some risks and high costs. Recently, Park et al. [13] fabricated transparent Y₂O₃ ceramics via SPS method, adding 3 mol% La₂O₃. The sintered sample showed excellent transmittance of 79.44% at a wavelength of 600 nm. However, SPS technology has the drawback of high equipment costs. Unfortunately, the use of a significant amount of sintering additives can alter the stoichiometry of the material, leading to the formation of a secondary phase that may separate from the boundary, ultimately resulting in a negative impact on transparency of ceramics [18].
Hence, to produce high-quality Y₂O₃ transparent ceramics by pressureless sintering, preparing nano-powder endowed with well sinterability is widely accepted as a critical process [19]. Among numerous preparation methods, the precipitation synthesis method is preferred for preparing ceramic powders due to its high yield and minimal equipment requirements [20]. Many studies on precipitation techniques for producing sinterable Y₂O₃ powders often utilize additives, including SO₄²⁻-ions, as dopants to achieve dispersion and regulate the shape of the resulting Y₂O₃ powders [21-29]. Zhang et al. synthesized nano-Y₂O₃ powders with weak agglomeration by calcining hydroxyl-carbonate precursors obtained from a spray co-precipitation technique. The mean particle size of the powders calcined at 1250 ℃ was approximately 140 nm. (NH₄)₂SO₄ was used as a regulator during the process. The Y₂O₃ ceramic, subjected to vacuum sintering at 1800 ℃ for 8 h, demonstrated an in-line transmittance of 78.7% at a wavelength of 1064 nm [29]. Our earlier study [30] examined the impact of introducing doped SO₄^2--ions to a commercially available Y₂O₃ powder. This process involved treating the starting powders with sulfuric acid. Loosely agglomerated and sinterable powder upon calcination was obtained from the powders treated with 7 mol% sulfuric acid and calcined at 1100 ℃ for 4 h. This was due to the presence of a single layer coverage of SO₄²⁻-ions on the surfaces of the particles, which inhibited the formation of hard agglomerates by facilitating the movement of particles during the calcination process, leading to particle coarsening.
Moreover, it is noted that the exploration of the sintering process kinetics of ceramic powder, especially at the initial sintering stage, holds significant importance for improving sintering technology [31]. Numerous researchers have previously examined the initial sintering of various ceramic powders, and various sintering-rate equations utilized for kinetic analysis during the initial sintering stage have been reported [32-37]. By utilizing sintering models, it is feasible to determine the mechanism, the activation energy of the process, and various other physical constants of the system. Among them, the assessment of quantitative densification during the initial sintering stage, executed under constant rate of heating (CHR), is widely acknowledged. Koji Matsui et al. studied the kinetic behavior of the initial sintering stage in Y-TZP powders doped and undoped Al₂O₃ [38]. The results showed that a minor quantity of Al₂O₃ increased the densification rate at the initial sintering stage, owing to a decrease in the activation energy of volume diffusions (VD) and a change of diffusion mechanism from grain-boundary diffusion mechanism (GBD) to (VD). Subsequently, he reported that the elevated Y₂O₃ concentration in fine zirconia powder led to a increase in the activation energy of GBD [39]. Prior endeavors have mostly concentrated on investigating the impact of synthetic conditions on the properties of Y₂O₃ powders. Nevertheless, the sintering kinetics of Y₂O₃ ceramic nano-powders, vital for producing densely packed ceramics, have yet to receive sufficient attention.
The present study focused on obtaining Y₂O₃ nano-powders with varying morphologies and particle size distribution (PSD) through calcination, both with and without the addition of sulfuric acid. This study employed constant rates of heating (CRH) to examine the influence of sulfuric acid doping on the sintering kinetics of nano-Y₂O₃ powders during the initial sintering stage. Additionally, the microstructure and optical properties of as-prepared ceramics that were vacuum-sintered were thoroughly analyzed to detect the sintering behaviors of the powders.

Preparation process
The starting material for this research was commercially available Y₂O₃ powder, a 99.99% purity level, acquired from Huizhou Ruier Rare Chemical Hi-Tech Co., Ltd., Huizhou, China. This powder exhibited a Brunauer-Emmett-Teller (BET) surface area of 31.5 m²/g. Two distinct batches of Y₂O₃ powder were prepared: one undoped and the other doped with 7 mol% sulfuric acid. The sulfuric acid concentration was calculated based on the molar percentage relative to the Y₂O₃ powder. Both powders groups underwent ball-milling, drying, and sieving through a 200-mesh nylon sieve. For comprehensive details, refer to our prior publication [30]. In atmospheric conditions, the so-obtained powders were calcined at 1100 ℃ for 4 h. Subsequently, they were uniaxially pressed into green compacts at a pressure of 100 MPa and then cold isostatically pressed at 200 MPa. The green compacts finally underwent sintering at 1500 ℃ and 1700 ℃ for 5 h in a vacuum furnace equipped with a molybdenum heating element (VSF-7, Shenyang, China).
Characterization
High-resolution transmission electron microscopy (TEM), employing a JEM-2100F microscope from JEOL, Tokyo, Japan, was utilized to examine the morphologies of the calcined Y₂O₃ powders.
Phase identification of calcined Y₂O₃ powders was carried out through X-ray diffractometry, employing a Philips Model PW3040/60 instrument based in Eindhoven, The Netherlands. Operating conditions for the XRD included a current of 40 mA, alongside the use of graphite monochromatic CuKα radiation (λ=0.15406 nm). Particle size distribution was analyzed utilizing LA-920 particle size analyzer (HORIBA, Japan), with distilled water serving as the dispersing medium.
The densification of powder compacts was evaluated in an oxygen environment (flow rate: 20 mL/min) via dilatometry using a thermal mechanical analyzer (SETSYS Evolution 2400, Setaram, Caluire, France). The analyzer maintained a constant heating rate from 2.5 ℃/min to 20 ℃/min, reaching a maximum temperature of 1600 ℃.
The green density of the green compacts was calculated using the geometric measurement technique. The density of the sintered bodies was determined through the Archimedes method, employing deionized water as the immersion medium at ambient temperature. Subsequently, the relative density was calculated by comparing the actual density of the sintered bodies with the theoretical density of Y₂O₃.
The in-line transmittance of the polished ceramic specimens, which were 1.5 mm thick, was evaluated utilizing a UV/Visible/NIR spectrophotometer (Model Lambda 750S, Perkin Elmer, CT, US).
A scanning electron microscope was employed to analyze the fracture surfaces of vacuum-sintered specimens. In order to prevent surface charge effects, especially at high magnification and voltage, prior to observation, the samples were uniformly coated with a gold layer.

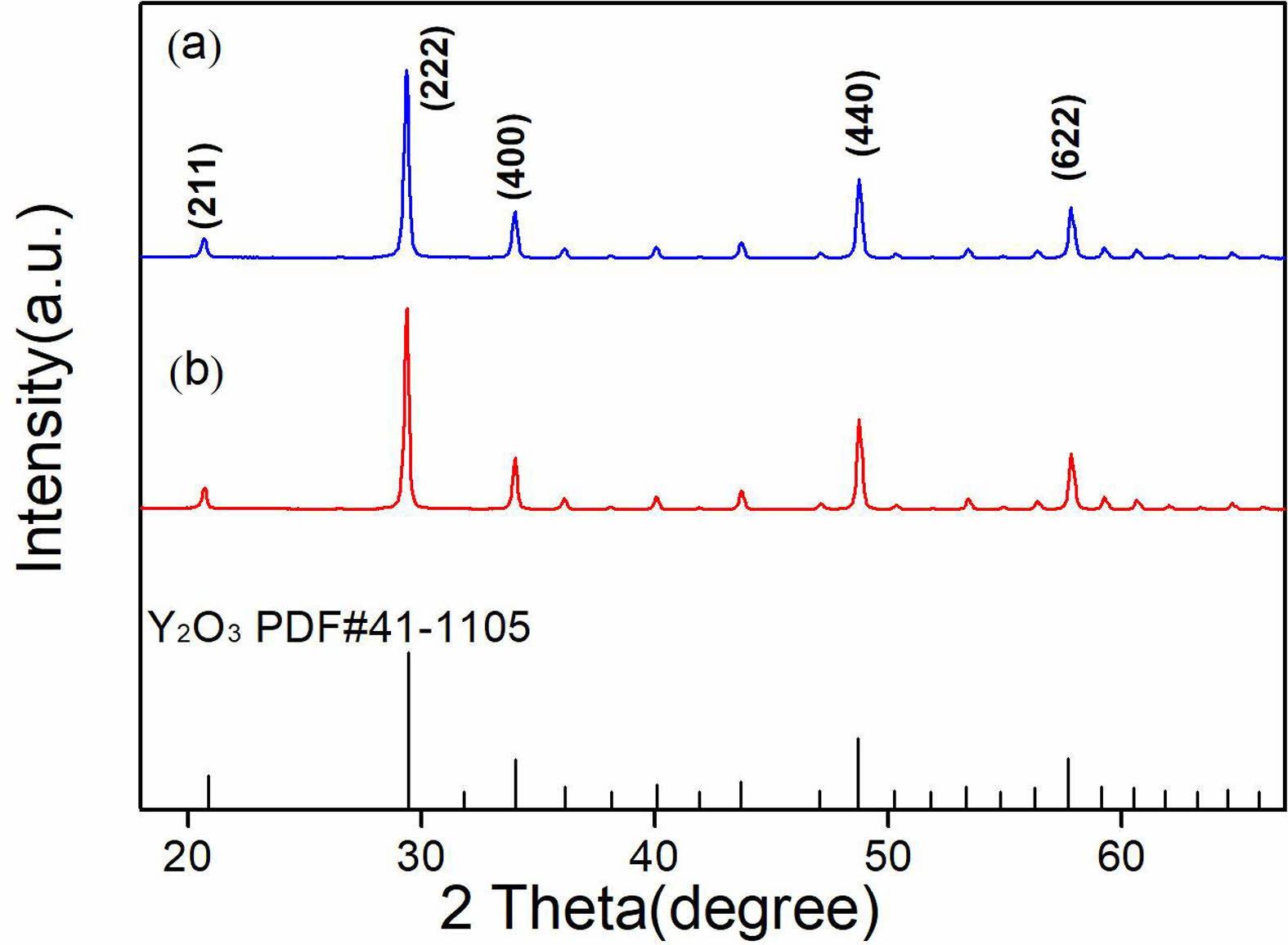
Figure 1 presents the XRD patterns of calcined Y₂O₃ powders, undoped (a) and doped (b) with sulfuric acid. The XRD patterns exhibited a similarity, corresponding to the cubic yttria phase (JCPDS#41-1105). Both characteristic diffraction peaks were sharp, indicating a high degree of crystallinity. Additionally, the results suggest that including sulfuric acid did not affect the formation of the Y₂O₃ phase.
Figure 2 illustrates the morphologies of Y₂O₃ powders that were calcined at 1100 ℃ for 4 h. A comparison is made between the undoped powder (Fig. 2(a)) and the powder doped with sulfuric acid (Fig. 2(b)). Figure 2(a) shows that the powders mainly consisted of severely agglomerated and irregular particles, with sharp edges and flat surfaces. The average particle size (d_TEM) was approximately 107 nm. However, when sulfuric acid was used, the resulting powders were less-aggregated and more evenly dispersed. As illustrated in Fig. 2(b), the powders exhibited an average particle size (d_TEM) of approximately 90 nm. Additionally, most particles exhibited round surfaces, indicating a relatively isotropic structure.
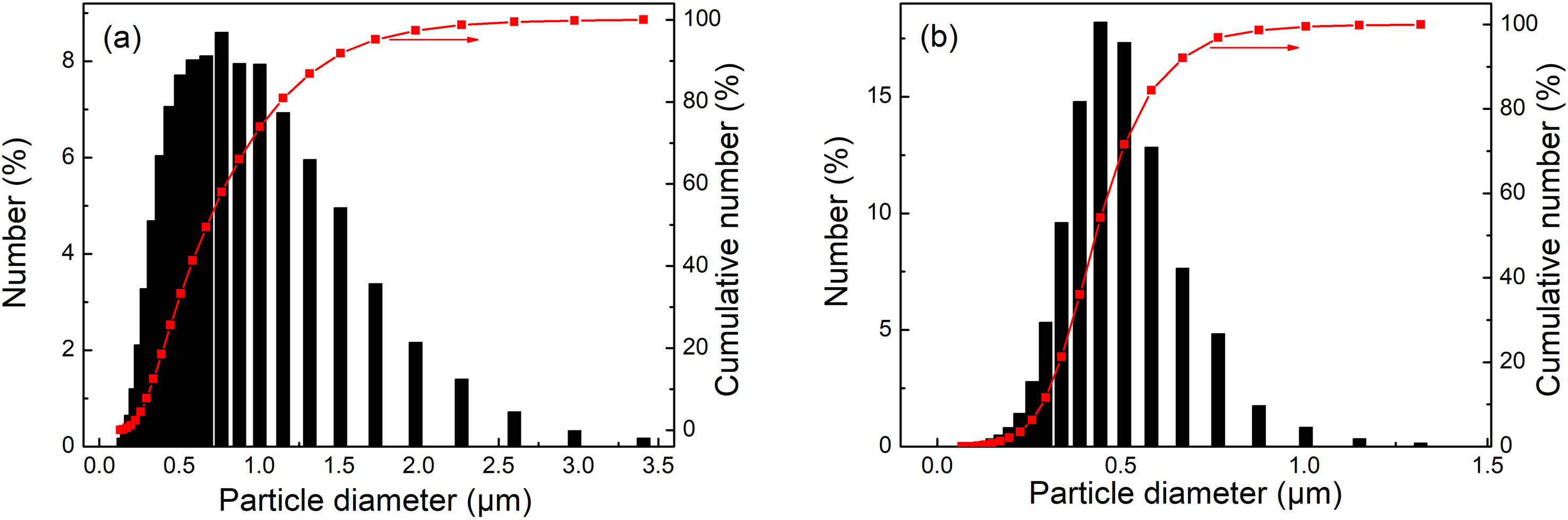
Figure 3 displays the particle size distribution and the cumulative particle size of the as-calcined powders, both undoped and doped with sulfuric acid. Both powders exhibited a single-mode distribution. Despite the small diversity of the primary particle size between undoped and doped Y₂O₃ powders (as shown in Fig. 2), there is a notable difference in the average agglomerate size. The undoped Y₂O₃ powder produced agglomerates with a maximum diameter of 3.4 µm (mean particle size D50 = 0.79 µm). Conversely, the as-doped Y₂O₃ powders had a narrower size distribution and a smaller D50 of 0.45 µm, indicating a more loosely agglomerated state. The particle size of doped Y₂O₃ powders is smaller than that of undoped ones, suggesting that adding sulfuric acid as a dopant significantly decreased the agglomeration degree of the powders during the calcination process. As demonstrated in our prior work, adding sulfate can effectively inhibit mass transfer processes associated with densification. Consequently, the addition of sulfate into Y₂O₃ powder during the calcination process contributed to a pronounced tendency towards particle coarsening, ultimately yielding Y₂O₃ powder with significantly reduced agglomeration [30].
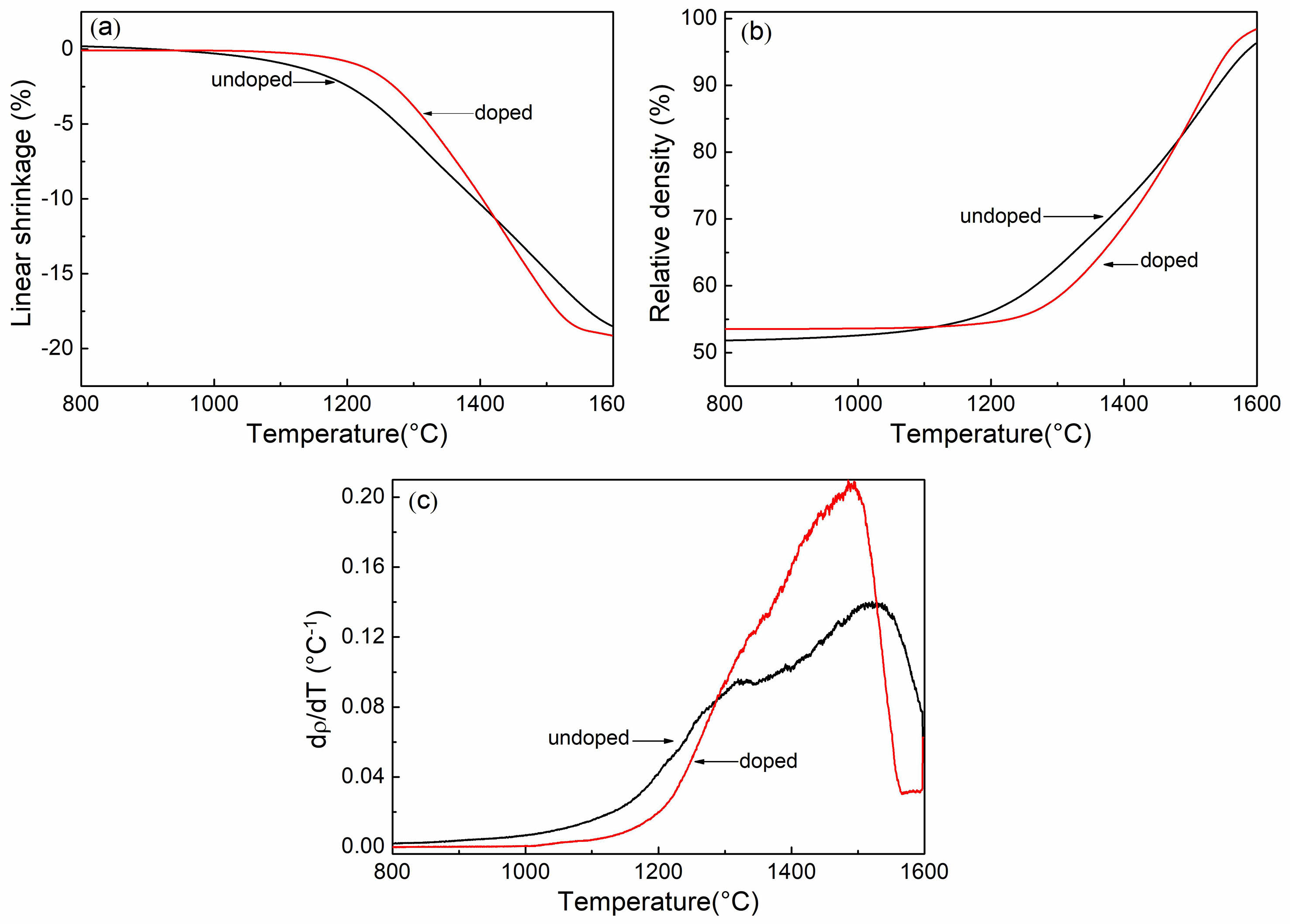
To investigate the impact of sulfuric acid on the sintering rate, the shrinkage behavior of green compacts made from both undoped and doped Y₂O₃ powders in a constant heating rate was examined, using a dilatometric method. Fig. 4 shows the shrinkage curves for a heating rate of 2.5 °C/min. As discernible from Fig. 4(a), the doped Y₂O₃ started shrinking at a slightly higher temperature (~1170 ℃) in comparison to the undoped Y₂O₃. Furthermore, beyond ~1425 °C, the doped Y₂O₃ demonstrated a higher degree of shrinkage in contrast to the undoped Y₂O₃. The total shrinkage was 18.4% for the undoped Y₂O₃ and 19.2% for the doped Y₂O₃. By analyzing the shrinkage curves in Fig. 4(a), the change in relative density (ρ) and densification rate (dρ/dT) with respect to sintering temperature was determined using Eq. (1) [31].



The density (ρ) of the powder compact at any given sintering temperature can be calculated using the initial green density (ρ₀) and the measured linear shrinkage (∆L/L₀). Here, L₀ represents the initial sample length; ∆L = L-L₀, L is the instantaneous sample length. As shown in Fig.4(b), At temperatures below 1250 °C, undoped Y₂O₃ exhibited a more rapid increase in relative density compared to doped Y₂O₃. The relative density of doped Y₂O₃ was higher than that of undoped Y₂O₃ at higher temperatures exceeding ~1480 ℃, and attained 98.4% of the theoretical density at 1600 ℃. Additionally, Fig. 4(c) illustrates the sintering temperature at which the densification-rate of undoped Y₂O₃ reached its maximum value shifted to a higher temperature of 1510 ℃ than that of doped Y₂O₃.
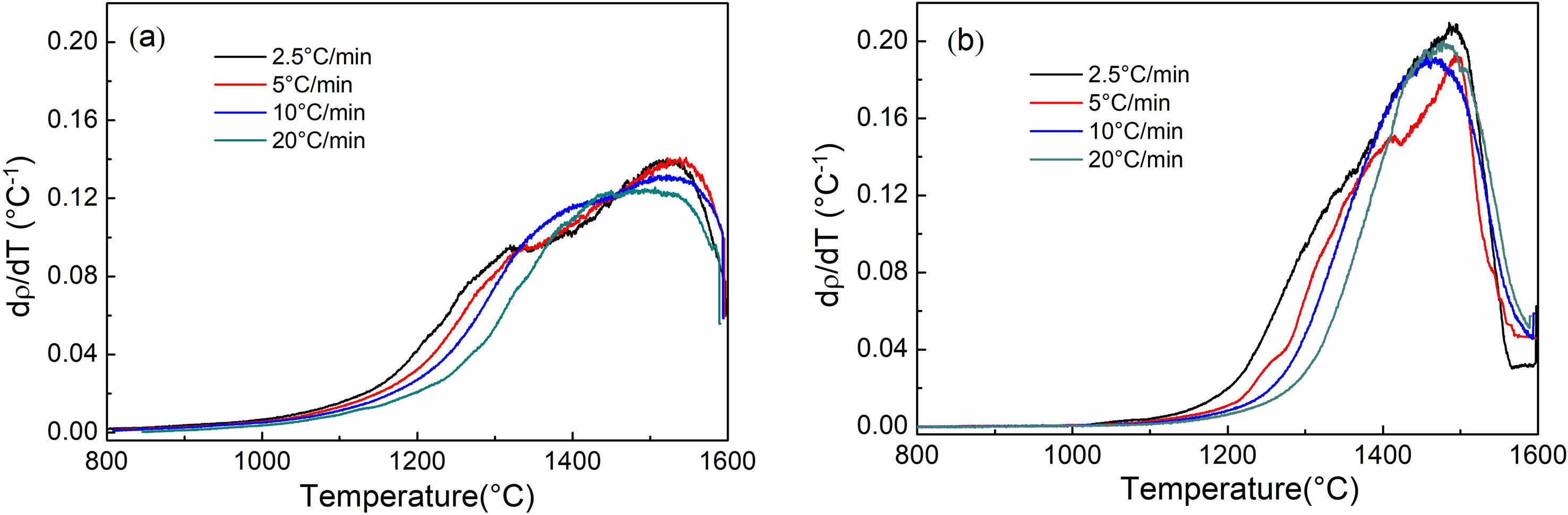
Figure 5 illustrates the densification rates of Y₂O₃ powders as a function of sintering temperature. These rates were observed at heating rates ranging from 2.5 to 20 ℃/min, and there was a noticeable shift in the densification rate curves toward higher temperatures, correlating with increased heating rates. At temperatures below ~1350 ℃, the doped Y₂O₃ exhibited a lower densification rate rather than the undoped Y₂O₃, regardless of the heating rate. However, beyond this temperature, the doped Y₂O₃ showed a higher densification rate, reaching 0.18 ℃^-1 at approximately 1460 ℃, employing a heating rate of 10 ℃/min.
Wang and Raj introduced the sintering-rate equation (Eq. 2) [33, 34], which has been employed to quantitatively evaluate shrinkage and shrinkage rate data, employing the constant rate of heating (CRH) method [40].



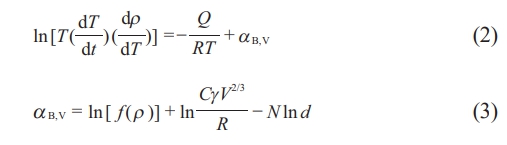
In this study, the variables used are as follows: ρ represents the density obtained from Eq. (1), Q represents the activation energy, and T represents the absolute temperature. R, C, and V are the gas constant, a constant, and the molar volume, respectively. The function f(ρ) is only dependent on density. In these models, d and N symbolize the grain size and its power law exponent, respectively. Equation (2) is applicable for fractional shrinkages below 4%, during which the initial sintering stage occurs without grain growth. A fractional shrinkage of less than 4% corresponds to a relative density range from 54% to 58% for the green compacts investigated in this study.
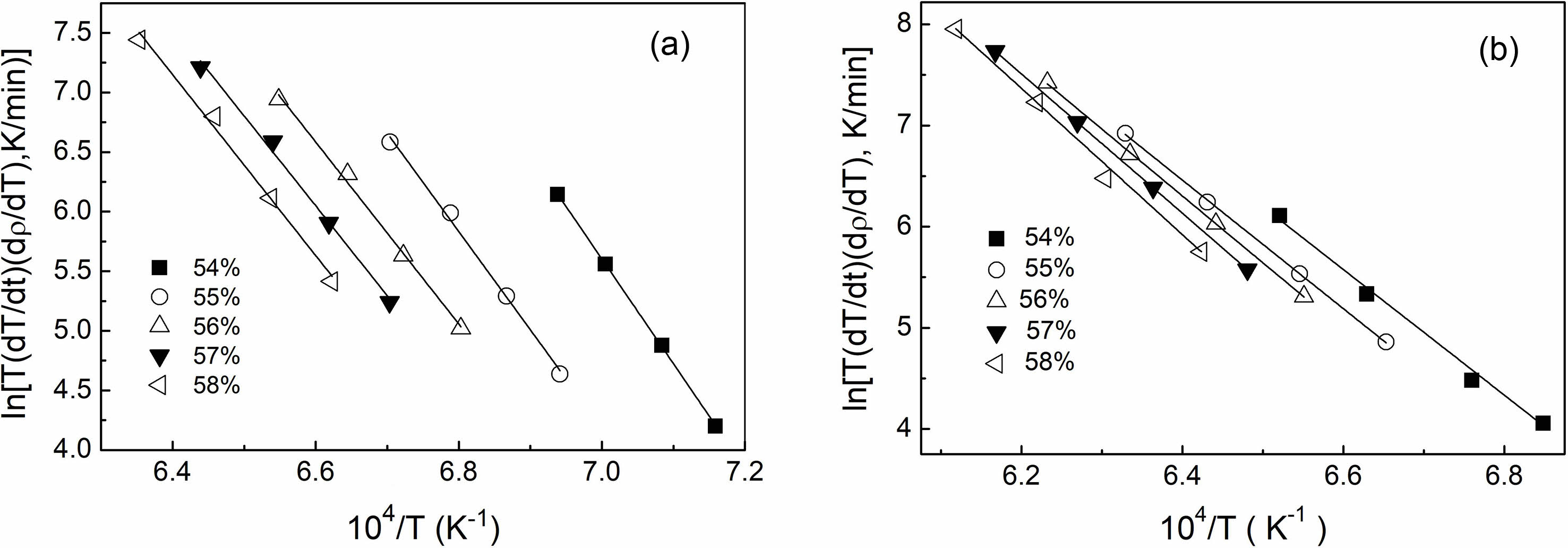
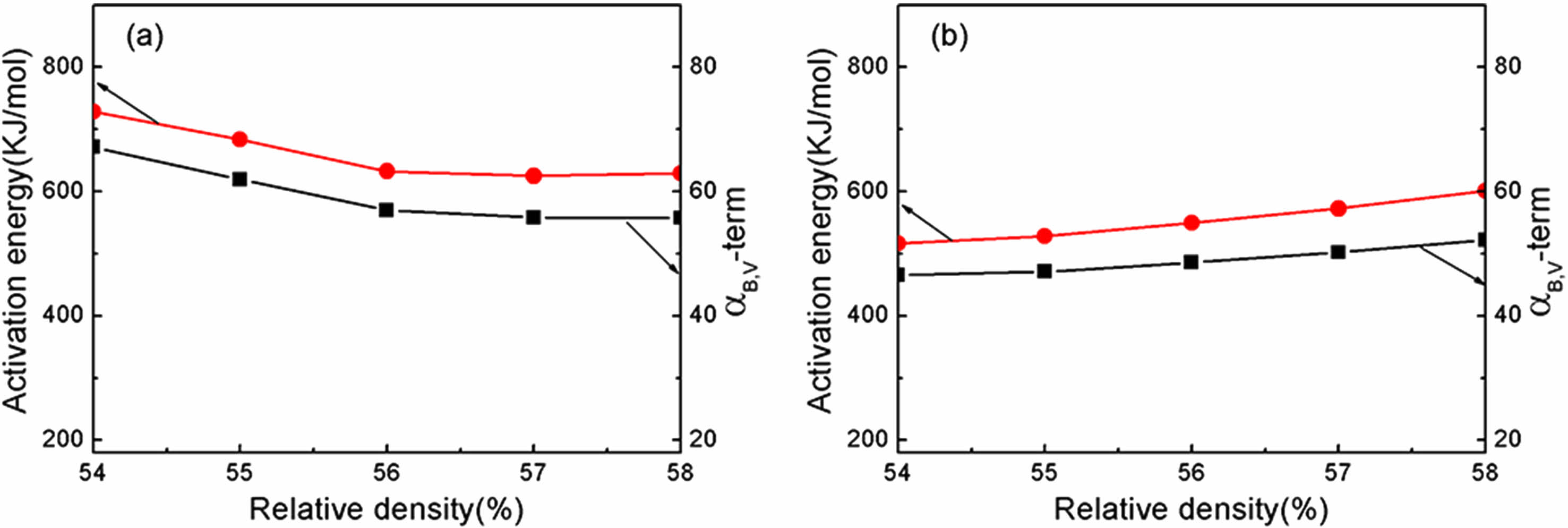
Based on the results of the densification rate of undoped and doped samples at various heating rates provided in Fig. 5, the activation energy (Q) value at each relative density can be estimated from the slope of an Arrhenius-type plot of ln[T(dT/dt)(dρ/dT)] against 1/T, as displayed in Fig. 6. The value of α_B,V term was also derived from the intercept of the straight line in the plot. Fig. 7 displays the activation energy and α_B,V term for the relative density range between 54% and 58%. The undoped Y₂O₃ exhibited significantly larger activation energies (Q) and α_B,V term compared to the doped Y₂O₃ at each given relative density. The average activation energies for both samples were likewise calculated within the relative density range of 54% to 58%, as shown in Table 1. The undoped Y₂O₃ had a Q value of 656 kJ/mol, whereas the doped one only displayed a Q value (553 kJ/mol). Wang calculated the activation energy of a Y₂O₃ ceramic to be 410 kJ/mol [41]. In this study, the activation energies are much higher than this value, possibly due to the discrepancy of the analysis model and the particle size of powders. The agglomeration state of powder significantly impacts the activation energy required for the initial sintering process. The initial sintering process between primary particles for the doped Y₂O₃ with low-agglomerated particles only necessitates a low sintering temperature and activation energy because of the short diffusion distance between these particles. In the case of hard agglomerated powder for undoped Y₂O₃, the sintering process within these particles facilitates the formation of dense particles with larger particle sizes, increasing the diffusion mass transfer distance and eventually requiring a higher activation energy for sintering. The present results demonstrated that the addition of sulfuric acid to Y₂O₃ powder reduced the average activation energy during the initial sintering stage.
To determine the diffusion mechanism of undoped and doped Y₂O₃ powder during the initial sintering process, the activation energies of both powders were calculated using the sintering-rate eqs. (4) and (5), as given by Young [33].



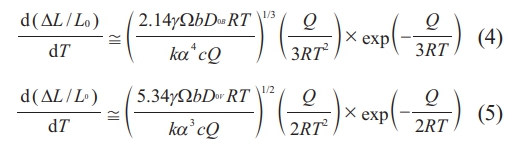
Here, eqs. (4) and (5) are employed to represent grain boundary diffusion (GBD) and volume diffusion (VD), respectively. Q is the activation energy for GBD or VD, γ denotes surface energy, Ω is atomic volume, bD_B is the coefficient for GBD, bD_v is the coefficient for VD, t represents time, T for absolute temperature, k for the Boltzmann constant, c for the heating rate (dT/dt), and α for the particle radius of powder.
By applying eqs. (4) and (5) to the shrinkage data obtained through the CRH technique, the apparent activation energy Q/m can be calculated by analyzing the slope of the plot of ln[T ^5/3 d (∆L/L₀)/dT] or ln[T ^3/2 d(∆L/L₀)/dT] versus 1/T (GBD- or VD-type plot) [38], by assuming GBD or VD. Additionally, applying eqs. (4)-(5), the order (m) associated with the diffusion mechanism was determined during the initial sintering stage, as expressed in eq. (6).



The value of m is 3 when sintering is regulated grain boundary diffusion and 2 when it is controlled by volume diffusion.
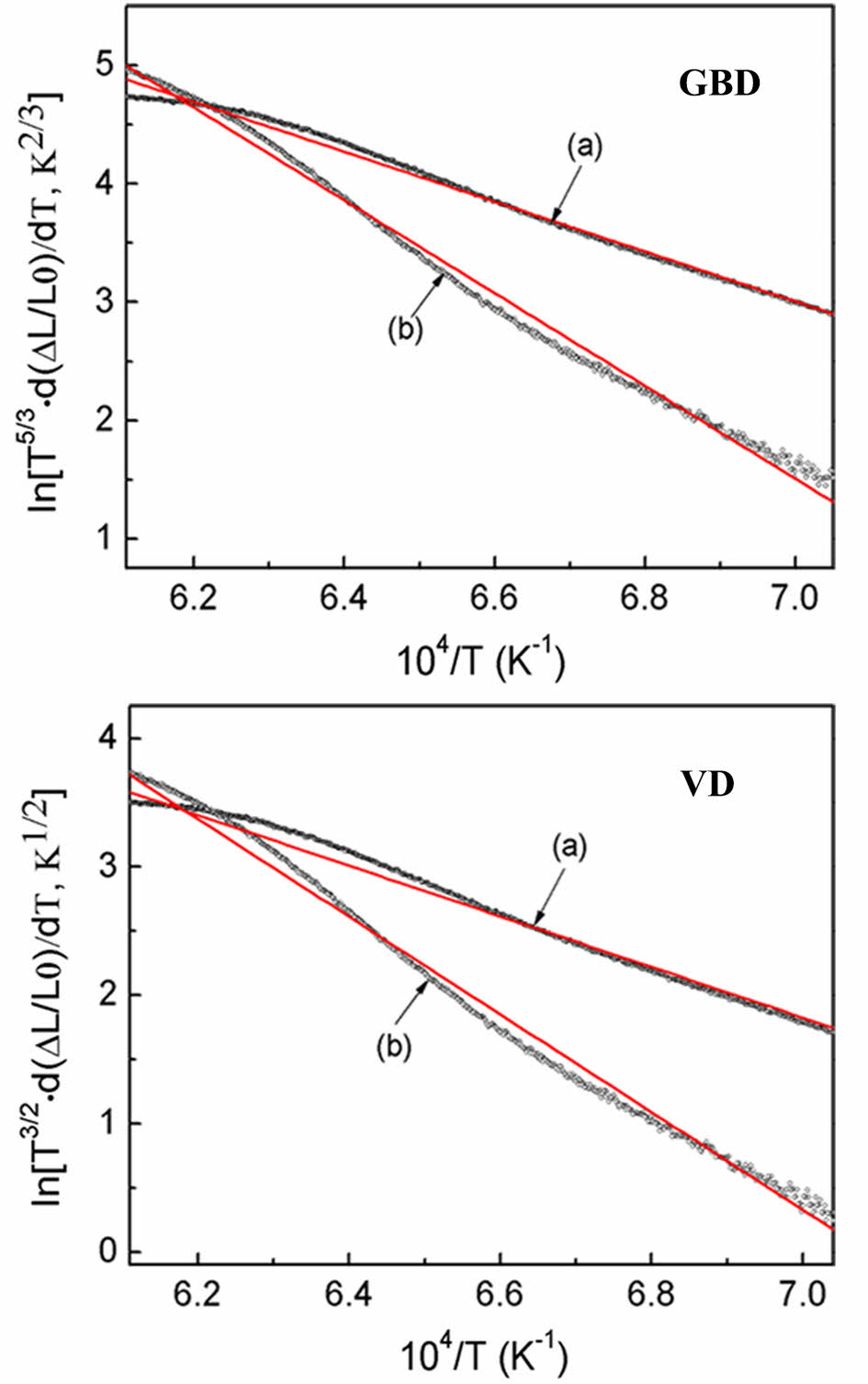
Figure 8 displays the GBD- and VD- type plots for Y₂O₃ powders, employing a heating rate of 2.5 ℃/min. The slopes for doped Y₂O₃ exhibited a higher magnitude compared to the undoped Y₂O₃, indicating an increase in the apparent activation energy during the initial sintering stage, due to the introduction of sulfuric acid doping. The average apparent activation energies (Q/m) were calculated for heating rates ranging from 2.5 to 20 ℃/min, as detailed in Table 1. Eq. (6) was employed to determine the order (m), thereby elucidating that the diffusion mechanism during the initial sintering stage was investigated by evaluating the Q values and the Q/m ratio. The values of m for the (GBD) and (VD) of the undoped sample were approximately 3.3, approaching the m value of GBD, which is m = 3. This observation implies that the diffusion mechanism for undoped Y₂O₃ can be ascribed to GBD. The m value of the doped Y₂O₃, which was nearly 1.8, revealed a strong correlation with the m value characteristic of VD (m = 2), indicating that the sintering mechanism was dominated by VD. It is widely recognized that the activation energy required for GBD of oxide ceramics is lower than that of VD [38]. Therefore, it is hypothesized that the activation energy for VD in undoped Y₂O₃ exceeded 656 kJ/mol, based on the activation energy obtained (656 kJ/mol) for GBD in undoped Y₂O₃ using the present CRH shrinkage analysis. Unlike the general tendency above, the addition of sulfuric acid caused a shift in the diffusion mechanism from GBD to VD during the initial sintering stage. This change is evident in Table 1 and yielded a lower activation energy for VD (553 kJ/mol) in doped Y₂O₃ rather than that for GBD in undoped Y₂O₃. These results further suggest that the addition of sulfuric acid directly impacts the diffusion process during the initial sintering stage of nano Y₂O₃ powder. Interestingly, as observed in Fig. 4, compared to the undoped Y₂O₃, the doped Y₂O₃ exhibited a higher onset temperature of shrinkage, which contrasted with the activation energy of both Y₂O₃ powders. Our previously published research has revealed that when the calcination temperature of the powder reached 1100 °C, there were still sulfur residues in the powders. Under high-temperature conditions, the decomposition of these residues initiated a mass transfer mechanism that promoted the loose growth of the powder particles rather than densification, ultimately elevating the sintering temperature at which the doped powder began to shrink.
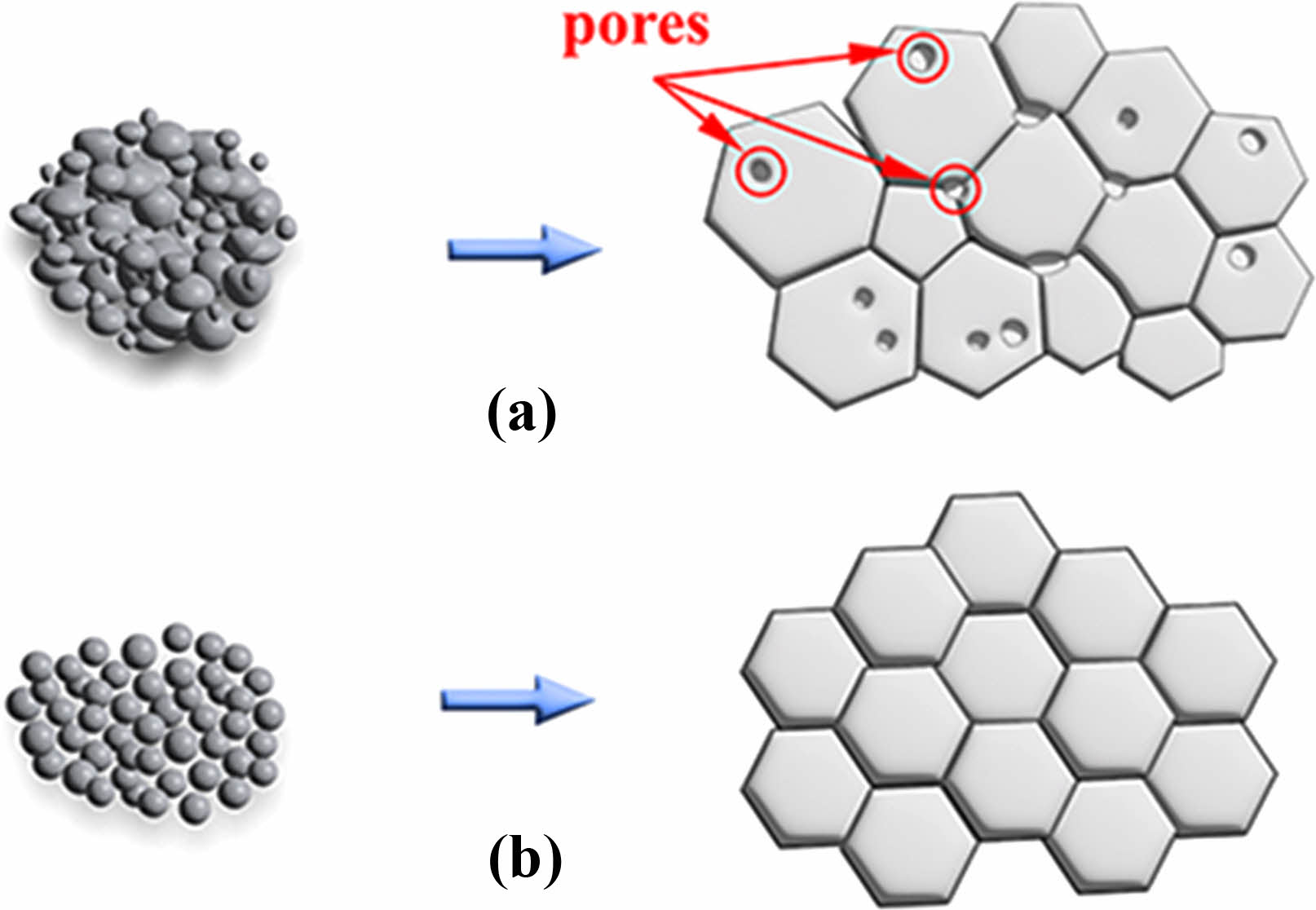
Figure 9 displays the microstructure of the fracture surfaces of Y₂O₃ ceramics sintered at a temperature of 1500 ℃ for 4 h in a vacuum atmosphere. The sintered ceramic produced from undoped Y₂O₃ powders contained a mass of pores within the grains and at the grain boundaries. This is attributed to the significantly elevated activation energy of the agglomerated Y₂O₃ powder. Despite employing high sintering temperatures in the final sintering stage, effectively eliminating these pores, which were wrapped in the grains, proved challenging. Moreover, the sintered ceramic obtained from doped Y₂O₃ powders possessed a well-defined microstructure, and only a few pores were observed (Fig. 9(b)), demonstrating their exceptional sintering activity. The enhanced sintering activity of doped Y₂O₃ can be attributed to its reduced activation energy during the initial sintering stage. The above results can be illustrated in Fig. 10, which is a schematic illustration of microstructures for undoped powder and doped powders and their resultant ceramics.
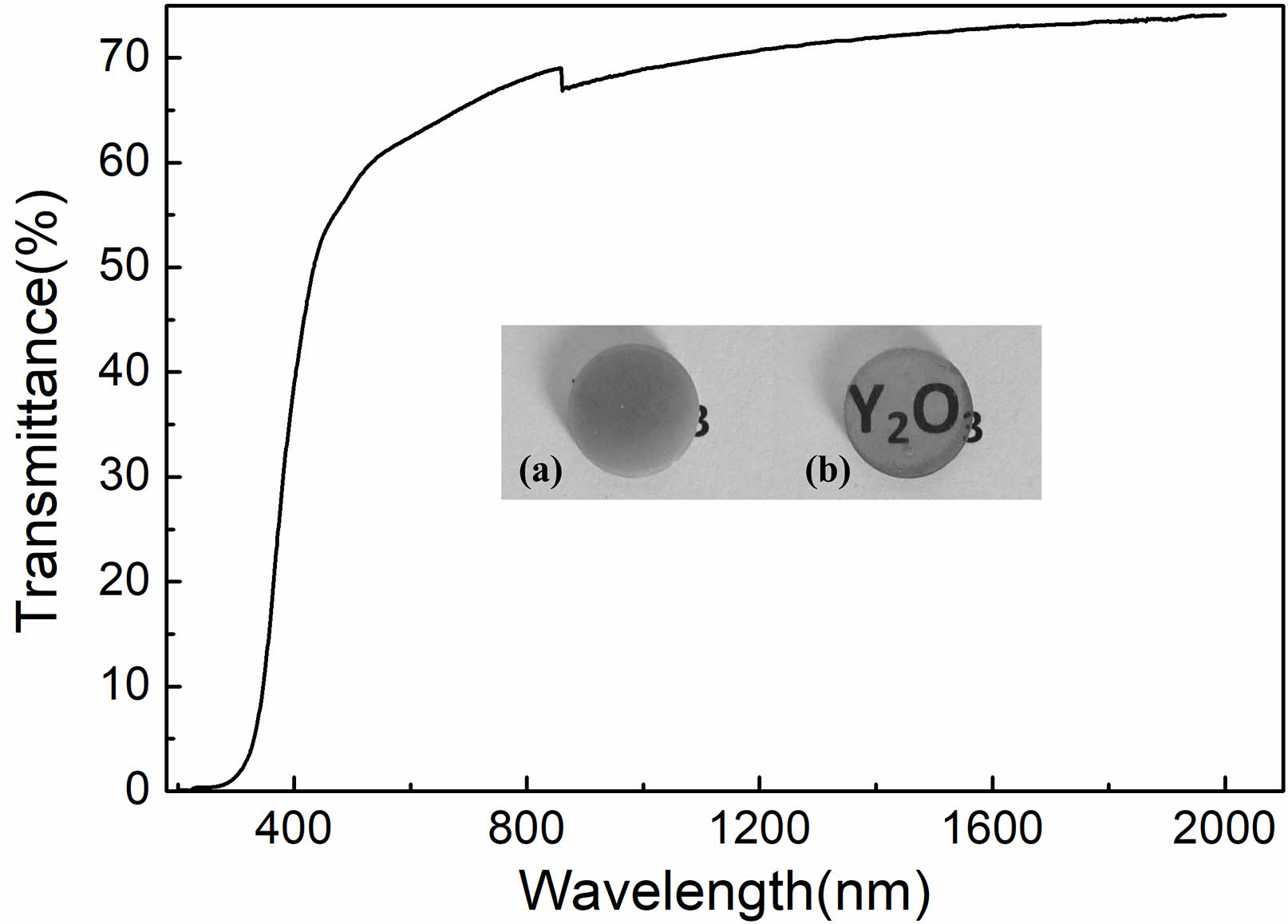
The mirror polished Y₂O₃ ceramic, derived from doped Y₂O₃ powder, had a thickness of 1.5 mm. The spectral transmittance of the ceramic was quantified across a wavelength range of 200 to 2000 nm, as shown in Fig. 11. The transmittance of the ceramic increased as the wavelength increased, reaching approximately 70% at 800 nm and 74% at 2000 nm. Conversely, the Y₂O₃ ceramic obtained from undoped Y₂O₃ powders was opaque, as shown in the inset picture in Fig. 11. The high transparency of the Y₂O₃ ceramic from doped powders further suggested that introducing sulfuric acid can effectively improve the sinterability of Y₂O₃ powders.

Transparent Y₂O₃ ceramics were prepared from nano-sized, sulfuric acid-doped Y₂O₃ powders using a vacuum sintering method. The doped Y₂O₃ powders revealed particles of finer size and less aggregates instead of the undoped Y₂O₃ powders. The sintering behaviors of powder compacts at the initial sintering stage were assessed using the CRH method. The addition of sulfuric acid remarkably increased the densification rate of Y₂O₃ powders, especially above ~1350 ℃, yielding a decline in the average activation energy (Q value) from 656 kJ/mol for the undoped Y₂O₃ to 553 kJ/mol for the doped Y₂O₃ in the initial sintering stage. Besides, it caused a shift in the diffusion mechanism from GBD to VD. Upon vacuum sintering at 1500 ℃, the ceramic for doped powders exhibited increased density and reduced residual pores compared to undoped one. In the case of the doped powder with sulfuric acid, a dense, transparent Y₂O₃ ceramic, with 74% transparency at 2000 nm wavelength, was achieved under vacuum sintering at 1700 ℃ for 5 h, unlike the opaque ceramic produced from undoped Y₂O₃.

This work was supported by the National Natural Science Foundation of China (Grant No. 51802136), Foundation of Liaoning Educational Committee (Grant No. L2020043).