Metal-based composites, such as those used in the aerospace and automotive industries, are becoming increasingly popular due to their intrinsic advantages like higher strength-to-weight ratios and less wear rates. An aluminium 7475 alloy based on MMC was tested using the Taguchi design of the experiment. The major goal is to use the Taguchi method to anticipate the best parameters for castings with the highest tensile strength and hardness. Good quality castings can only be made with precise control of the process parameters. Stir casting was employed to make test samples with varying reinforcement weight percentages, stirring speeds, and processing temperatures. Analytical variance and orthogonal arrays were used to explore the influence of process factors on the desired attributes. The Taguchi method was used to identify the best settings for maximizing the mechanical characteristics of composites. The fundamental objective of this investigation is to find how various parameters can be altered to produce defect-free castings with the necessary tensile strength and hardness for certain applications. The Taguchi optimization method was demonstrated by conducting a test at the optimal level of processing parameters

Keywords: Zirconium carbide, Alumina, Taguchi, Hybrid, Optimization, ANOVA

Composites made of the aluminium matrix are becoming increasingly popular due to their low density, larger specific strength, and exceptional resistance to wear and tear [1]. Adding discontinuous second-phase particles to aluminium alloys provides higher strength, higher modulus, better wear resistance, outstanding workability, more pleasing thermal expansion, and isotropy in terms of thermal expansion and strength [2, 3]. There is currently no monolithic material that can match the mix of qualities offered by AMCs, which is why they are called "superior". There have been several structural, non-structural, and functional uses for AMCs in the past in a variety of engineering fields [4-6]. Performance, economics, and environmental benefits are all important factors in the decision to use AMCs in these industries. Monolithic materials such as AA, Ti alloys, and polymer-based composites can be replaced by AMCs in various applications [7]. The matrix phase in AMCs is made up of aluminum/aluminum alloy, which forms a percolating network. Non-metallic and ceramics substances like ZrC and Al₂O₃ are widely utilized as strengthening in this aluminium alloy matrix. Materials like ZrC, Al₂O₃, and Gr are frequently utilized as particle reinforcements in MMC [8-10]. Composites strengthened with ceramic particles have good abrasion resistance. AMCs' parameters can be adjusted by altering the composition and volume fraction of their constituents. Less fuel usage, reduced noise, and reduced airborne emissions are three of the primary advantages of AMCs in transportation. Hybrid composites, in particular, were thought to have better characteristics than single-reinforced composites in this study [11-13].
Increased silicon carbide content results in an improvement in hardness and toughness, respectively, over the unreinforced aluminium alloy [14, 15]. When compared to unreinforced matrix metal, MMCs have a higher level of toughness. Increasing the wt.% of ZrCp in cast compounds results in a linear rise in hardness (silicon carbide particulates) [16]. The Cast composite's tensile strength improves with ZrCp weight percentage. Elongation reduces when the ZrCp content in the matrix metal increases, i.e. LM6. To improve wear resistance and reduce thermal expansion, a variety of hybrid composites have been developed in recent years [17, 18]. It is the addition of particles that has the greatest mechanical characteristics impact of PRAMCs (particulate-reinforced AMCs). The volume fraction (vf), size, figure, and dispersal of strengthened particles within the MMC are all important in the determination of the mechanical characteristics of PRAMCs [19]. As far as influencing factors go, the volume fraction is the most important (vf). Stir casting's greatest advantage is its capacity to produce massive quantities of product. For MMC production, stir casting is the cheapest method out of those that have been thoroughly tested. For mass manufacturing, stir casting can save as little as a third to a tenth of the cost of other methods. As a result, commercial stir casting is now the most extensively utilized technique for creating aluminium based composites [20-22].
Varying processing factors have an impact on composite material quality. When it comes to factors like particle size and percentage of reinforcement, there must be at least one or two that are more important than the others [23-25]. A manufacturing process can only operate at its maximum economic and technological capacity if its parameters are optimized. Taguchi method is a significant optimization approach [26]. High-quality systems can be designed with the help of the Taguchi approach [27]. Optimizing the efficiency of a Taguchi parameter design can lower the system's responsiveness to the source of variation through the use of predefined parametric settings. Individual and combination parametric settings can be learned from a small number of simulations using Taguchi's approach. To obtain a good understanding of the product or process performance, numerous stages must be performed [28-30].
The study focuses on the use of the Taguchi method to optimize the process parameters for the fabrication of AA7475/ZrC/Al₂O₃ hybrid composites, which are increasingly popular in the aerospace and automotive industries due to their high strength-to-weight ratios and low wear rates. The paper contributes to the field of materials science and engineering by providing a comprehensive analysis of the factors that affect the mechanical properties of these composites and identifying the optimal processing parameters for their fabrication.
The motivation of the article is to explore the use of the Taguchi method to optimize the process parameters for the fabrication of AA7475/ZrC/Al₂O₃ hybrid composites. The objective is to find how various parameters can be altered to produce defect-free castings with the necessary tensile strength and hardness for certain applications.
The developed composite has potential applications in the aerospace and automotive industries due to its high strength-to-weight ratio and low wear rates. The production process involves melting and solidifying the matrix alloy with dispersed reinforcing particles using the stir-casting method. The potential applications of the composite include structural components, engine components, and other applications that require high strength and low weight.
The distribution of reinforcing particles in the molten matrix during the stir casting process is affected by several factors such as mechanical stirrer shape and settings, particle properties, melt temperature, and the placement of the mechanical stirrer.
The matrix used in this study is made of AA 7475, which is melted and solidified to form a metal. Zirconium carbide and alumina particles are used as reinforcing materials, which are dispersed into molten aluminum using the stir-casting method.
There has been a lot of work done in characters improvement of aluminum MMCs by stir casting, according to the substantial literature review done for this research. Only a very small amount of research has been done to explain how AMCs' mechanical qualities, such as tensile strength, are affected. On AMCs properties, few studies have been done on the combination of alumina and Zirconium carbide (ZrC). Using the Taguchi approach, this study examined the tensile and hardness parameters of an Al 7475/Zirconium carbide/alumina hybrid compound made by altering stir-casting procedure parameters.

Methodology
The matrix in this investigation is made up of AA 7475. Table 1 lists the matrix alloy's chemical constituents in weight percent. Zirconium carbide (220 mesh) and alumina particles are used as reinforcing materials in this project.
The melting and solidification process of the matrix alloy involves first melting and then solidifying it. The introduction of the reinforcing particles affects the microstructure of the composite by enhancing the mechanical parameters of material matrix composites through the introduction of a scattered phase order. A strong interfacial connection (wetting) should be achieved between the dispersed phase and the melted matrix, which can be improved by covering the dispersed phase particles. Factors such as mechanical stirrer shape and settings, particle properties, melt temperature, and the placement of the mechanical stirrer all affect particle distribution in the molten matrix.
Metal is fabricated by first melting and then solidifying it. The mechanical parameters of material matrix composites are enhanced by the introduction of scattered phase order. During the procedure, a strong interfacial connection (wetting) should be achieved between the dispersed phase and the melted matrix. By covering the dispersed phase particles, wetting can be improved. Interfacial energy reduction is just as critical as preventing scattered phase interactions with the matrix. Reinforcing materials (typically in powder form) are dispersed into molten Al using a stir-casting method [31]. The stir-casting method has a major problem with the segregation of reinforcing particles during melting and casting. These particles are segregated because of the surfacing or settling of reinforcing particles. In the molten matrix, factors such as mechanical stirrer shape and settings, particle properties, melt temperature, and the placement of the mechanical stirrer all affect particle distribution. Fig. 1 displays the stir casting procedure utilized to make the AMCs which consists of a resistive heating furnace, a mechanical impeller powered by a variable speed motor, and a temperature-measuring thermocouple.
An electrical furnace melted a specific volume of matrix alloy to a temperature of 600 °C. In the preheating furnace, a precise amount of Al and ZrC powder was heated to 1000 °C for two hrs. With varied speeds and 10 minutes to create a vortex, the melt was churned inside the furnace to spread out the powder in the melted. The melting temperature was monitored and verified using thermocouples before diecasting in a carbon steel mold. Afterward, magnesium was introduced into the melted metal to create a better link between matrix alloy and strengthening particles. The fluidity of molten metal is also improved by the addition of pure magnesium. It was found by dividing the volume of the particles by the composite volume of the die, which was derived by taking their weight and density into account.
Application of the Taguchi method
Experiment design using the Taguchi method is a method for laying out trials in the most logical, cost-effective, and statistically sound manner [32]. The Taguchi technique steps are depicted in Fig. 2. Using Taguchi's parameters design method, it is possible to identify the parameters that have the best performance and efficiency. It saves time, money, and resources by eliminating the need for repeated trials. Table 2 lists the three parameters (A, B, and C) that were examined in the composite preparation procedure to determine the degree to which they influenced the final product, as well as their respective levels of influence. Several pieces of Literature were studied in this research [33, 34].
The Taguchi method is a statistical technique used for the optimization of a manufacturing or engineering process. It is based on the design of experiments and uses orthogonal arrays to explore the influence of process factors on the desired attributes. The Taguchi method has several advantages, including its ability to reduce the number of experiments needed to determine the optimal process parameters, its ability to identify the most significant factors affecting the process, and its ability to provide robustness to the process by minimizing the effects of noise factors. However, the Taguchi method has limitations, including its assumption of linearity of the process, its inability to explore interactions among process factors, and its inability to handle non-normal distributions.
It is common in industrial studies to use orthogonal arrays to examine the impact of multiple control parameters. An OA is formed when the interdependent variables' columns are orthogonal to one another. Using orthogonal arrays simplifies the investigation and saves a significant amount of time and money in the experiment. To define an OA, one needs to know the number of levels and factors involved. It was determined how many levels – 1 – each parameter has to calculate its degrees of freedom (DoF).
As a result:
• A, DoF = 3 – 1 = 2
• B, DoF = 3 – 1 = 2
• C, DoF = 3 – 1 = 2.
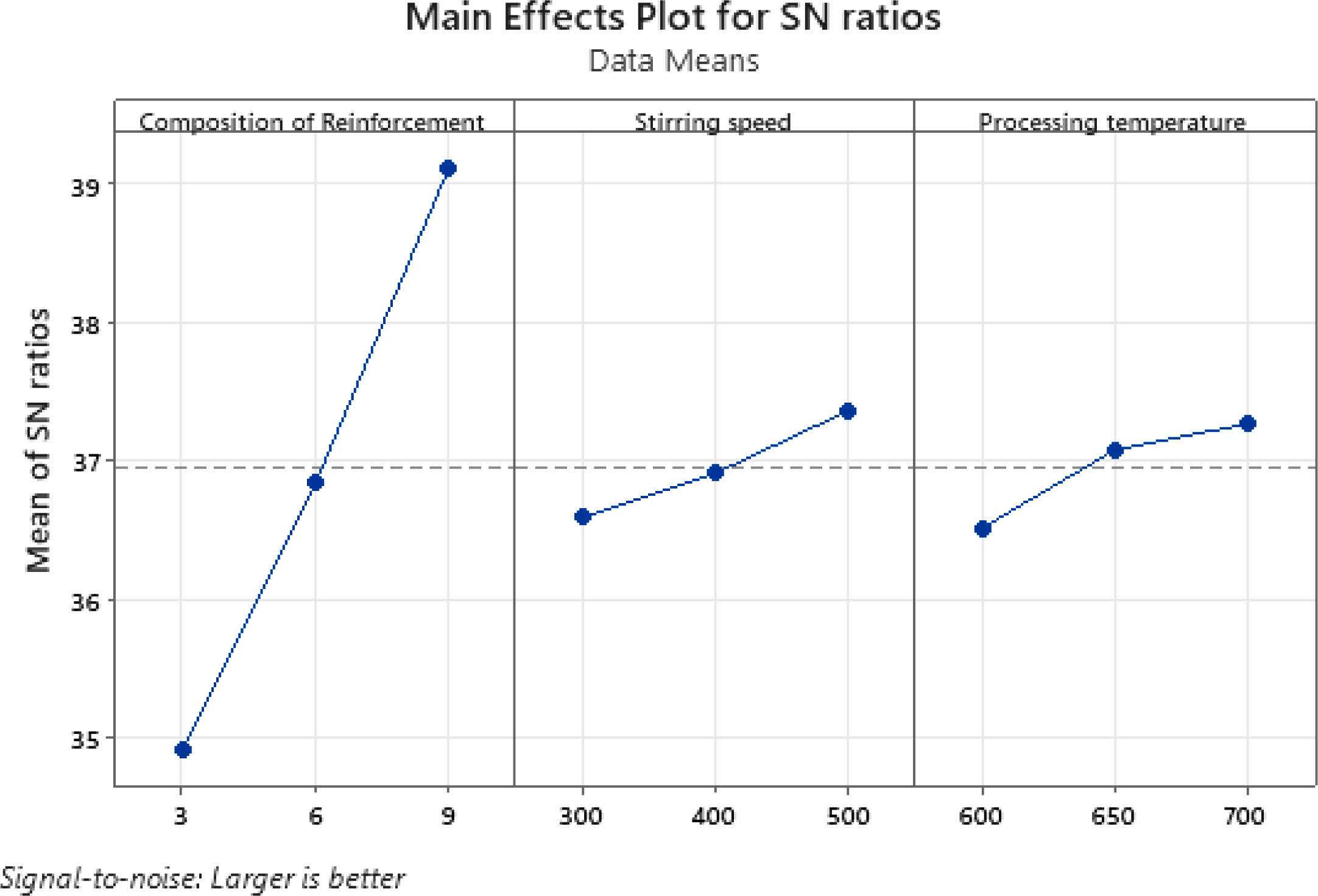
There were 9 experimental runs in an L9 orthogonal array, each with a three-level level. The experiment has a total of 8 DoF. The OA employed in this investigation is tabulated in Table 3. Stir casting was used to create nine pieces of hybrid composites using the process parameters illustrated in an orthogonal array in this study. ASTM E-8 standards were used to create the samples for TS and hardness tests, respectively, using a milling machine.
Table 3 presents an L9 Orthogonal array, which is a type of experimental design used in statistical analysis. The purpose of the design is to investigate the effects of multiple input parameters on a system or process, while minimizing the number of experiments required. In this case, the table presents the input parameters and corresponding values for 9 different experiments involving the processing of a composite material. The results of these experiments can be analyzed to determine the effect of each input parameter on the performance of the composite material.

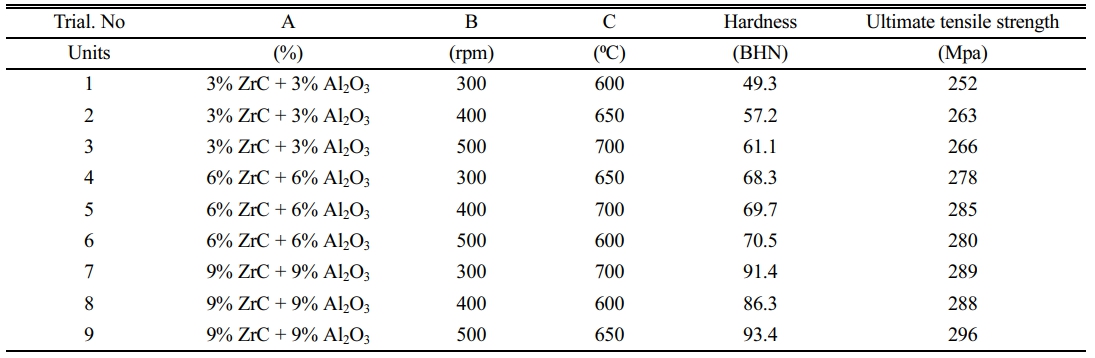
Results of Tensile Strength and Hardness
Metals' Brinell hardness can be measured with the ASTM E-10-98 standard test. Using a 5 mm diameter indenter ball, the applied stress is 250 kg, resulting in an indentation with a diameter of 2.5 to 6.0 mm in the sample. The weight is being steadily and methodically imparted. For 10 to 15 seconds, the whole load is applied. The specimen to be tested is clamped between the universal testing machine's two end jaws for tensile testing. The specimen is now subjected to a steadily increasing load via the movable crosshead until it breaks. During the test, the load measurement unit records the amount of force exerted (load cell). Table 4 shows the results of the Brinell hardness and tensile tests.
Design of experiments
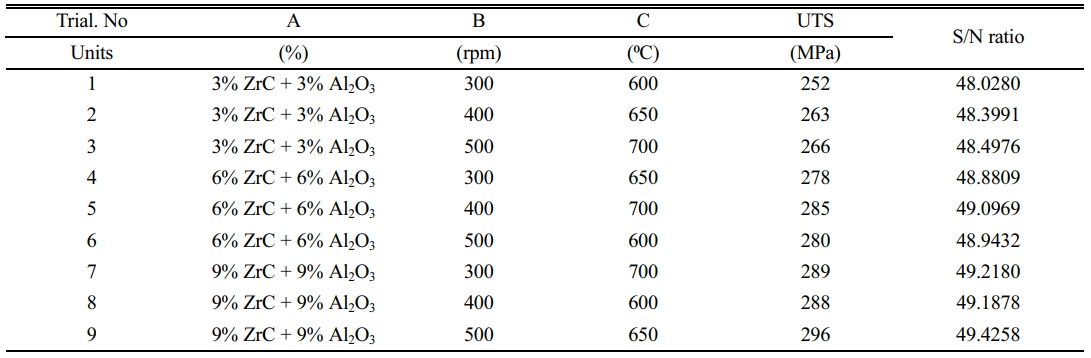
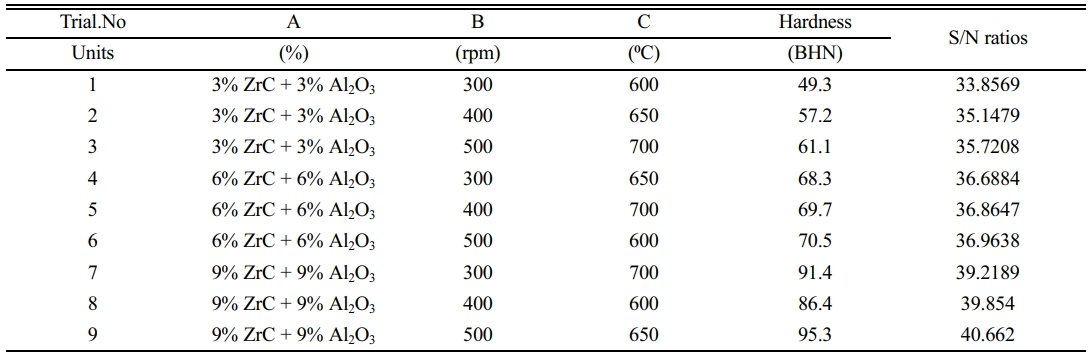
Quality characteristics can be improved by adopting Taguchi's method, which emphasizes studying response differences utilizing the S/N ratio. Using the Taguchi approach, "signal" denotes to desired mean, and "noise" denotes to unwanted value (standard deviation) for output quality attributes. It is the products in reaction to a determinant in experimental variables that provides a signal of the anticipated outcome. Noise is a term used to describe the influence of outside elements (uncontrollable variables) on the result of a quality properties test. The SNR for "larger is better" is used to forecast the ideal values in the current study since a greater composite hardness and tensile strength are desired. After the specimens were prepared by the L9 OA methodology, the SNR was calculated using the MINITAB software. Tables 5 and 6 illustrate the observed mechanical properties as a function of Equation (1).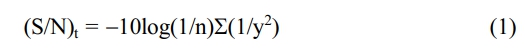



Table 4 shows the results of the Brinell hardness and tensile tests for various trial numbers, where the metals' Brinell hardness and ultimate tensile strength were measured.
Table 5 shows the tensile test results for each trial number, where the ultimate tensile strength (UTS) and signal-to-noise (S/N) ratio were measured.
Table 6 shows the hardness test results for each trial number, where the Brinell hardness and S/N ratio were measured.
The results suggest that increasing the percentage of ZrC and Al₂O₃ led to an increase in both hardness and tensile strength, with the highest values observed for trial number 9 with 9% ZrC and 9% Al₂O₃. The S/N ratios for both hardness and tensile strength also suggest that trial number 9 had the best performance.
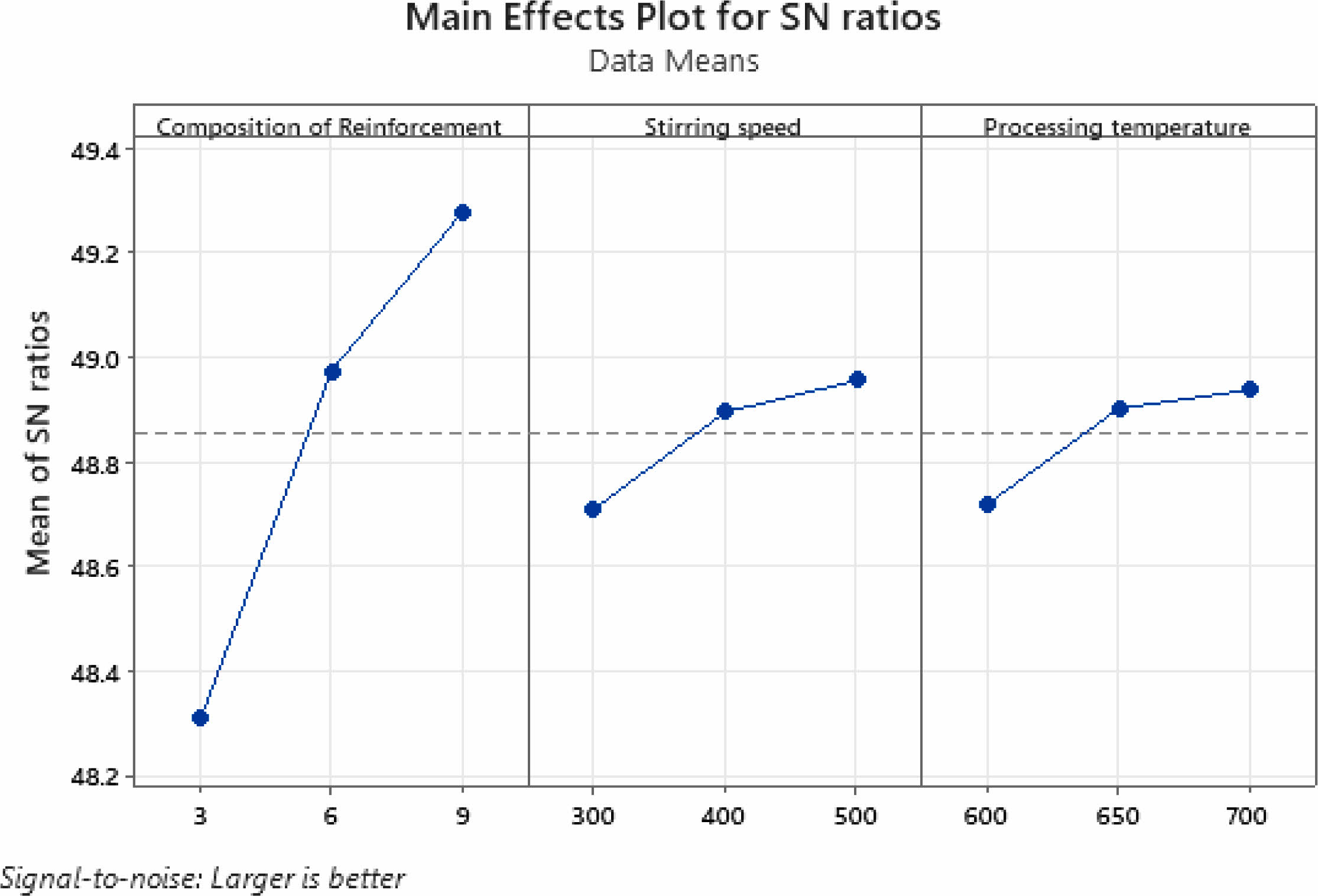
Main effect plots for the S/N ratio
Plotting changes in performance characteristics as a function of a process parameter's level is known as a "main effect." Three components and three degrees of material are depicted in Fig. 3 and Fig. 4 in the main effect graph.
The concept of a main effect plot is to visualize the relationship between a response variable and a categorical predictor variable. The response variable is a performance characteristic (UTS and hardness) and the predictor variable is a process parameter with three levels.
A main effect plot shows the mean response for each level of the predictor variable, and allows to compare the effect of each level on the response variable.
In Fig. 3 and Fig. 4, the main effect plots show how the UTS and hardness of the material change as the process parameter varies between its three levels. The plot for UTS in Fig. 3 suggests that the UTS decreases as the process parameter increases, while the plot for hardness in Fig. 4 suggests that hardness increases as the process parameter increases.
Optimum processing parameter settings
As a result of the responses, the best processing settings are provided in Table 7.
Analysis of variance
Process variables that have the greatest impact on a quality attribute can be identified using an ANOVA. Using ANOVA, it is possible to discover the optimal combination of process characteristics by examining their relative relevance. The MINITAB 14 software tool was used to conduct an ANOVA with a significance level of 6% to examine the contributions of the components. Each independent variable in the model has a P-value in the ANOVA table. The parameter is statistically important if P-value is < 0.05. At a 94% confidence level, it was determined that all three variables had p-values less than 0.05, making them extremely significant. Variable contributions are shown in Table 8 and Table 9 by their percentage of overall difference, indicating their impact on mechanical parameters. According to the analysis of variance results in Tables 8 and 9, increasing tensile strength and hardness is primarily dependent on weight reinforcement percentages.

A confirmation test concludes the experiment design procedure. For composites, the ideal variables for hardness and TS were discovered to be 18% reinforcement weight, 500 rpm stirring speed, and 700 ^oC. Experiments were carried out to find the best settings. The regression model's generated values were compared to the most promising results (the highest hardness of 90BHN and a UTS of 290 MPa). The regression equation predicts hardness and tensile strength values that are within 6% of the measured values. The resultant equations appear to be able to accurately predict mechanical properties. Errors could be reduced by increasing the number of performance standards that are being observed.

The mechanical characteristics of AA7475 ZrC-Al₂O₃ hybrid MMC were discovered to be influenced by the proportion of wt of strengthening, stirring speed, and processing temperature. ZrC and AA7475 were shown to be the most important variables in ANOVA, followed by stirring speed. For composites, the ideal variables for hardness and TS were discovered to be 18% reinforcing weight, 500 rpm stirring speed, and 700 ^oC. Particle size and wt.% of reinforcements also affect mechanical characteristics. The addition of reinforcements to the melt was made easier with a stirring speed of 500 rpm. The composite gains strength and hardness as tougher reinforcements are incorporated. Reinforcements become more wettable at higher temperatures, allowing for more consistent mixing. Future research could focus on exploring the interactions among process factors that were not explored in this study, such as the interaction between stirring speed and processing temperature. Future research could also investigate the effects of using different types and sizes of reinforcing particles on the mechanical properties of the composites.

No participation of humans takes place in this implementation process

No violation of Human and Animal Rights is involved.

No funding is involved in this work.

Conflict of Interest is not applicable in this work.

There is no authorship contribution

The authors would like to acknowledge the Researchers Supporting Project number (RSP2023R373), King Saud University, Riyadh, Saudi Arabia.