In this study, the effect of specific rates of breakage of nefelinli siyenit, which is a magmatic, feldspathic rock, on technological properties of ceramic bodies is examined. The ceramic material properties considered in this study derived from the application of non-destructive and destructive tests and include firing shrinkage, water absorption, mercury porosimeter and firing strength, while the specific rate of breakage (S_i) determined from batch grinding tests. In order to S_i values, in the range of -63+53 μm mono-size fraction was prepared. The nepheline syenite prepared in these interval were ground with 1/4, 5/16, 3/8, 1/2 and 3/4 inches alloy steel balls for different durations. The results indicate that the technological properties of ceramic materials examined show very good correlation and can be used to predict S_i. Overall, it is deduced that multiple regression analysis involving two independent variables is a reliable approach and can be used to identify correlations between technological properties of ceramic materials and specific rate of breakage values for nepheline syenite.

Keywords: Nepheline syenite, comminution, specific rate of breakage, ceramic materials, technological properties

Nepheline syenites are formed through a process that involves both ordinary magmatic separation and volatile enrichment. Nepheline syenites are alkali volcanic rocks that are magmatic in origin, and that crystallize at a very advanced stage of magmatic separation, while phonolites are their volcanic equivalents. Some of the Canadian deposits are known to have metamorphosed during regional tectonic events, while a metasomatic origin has been proposed for the older Livaara bed in Finland [1, 2]. Typically associated with alkali or carbonatite complexes, nepheline syenites have attracted considerable worldwide interest in both economic and academic circles. Economic nepheline syenite deposits that can be used in glass or ceramics are rare. Nepheline syenite deposits usually have a high iron content. The largest reserves can be found in Russia, Canada, Norway, Brazil, China and Turkey, all of which are major global producers. In 2013, nepheline syenite with a total value of $59.3 million (491,000 tonnes) was imported worldwide [1, 3, 4]. In Turkey, nepheline syenite is mined in the Buzlukdağı locality of the Akpınar district of Kırşehir province, 12 km from the Kırşehir-Ankara road. The visible nepheline syenite deposits in this field are 2,250 m long, 1,850 m wide and 450 m deep, and have properties suitable for the tile, vitrified tile, frit, porcelain, glass, insulator, cement, insulation and electrode sectors.
Feldspathic materials have been the main melters used in the ceramic sector for hundreds of years. In this highly competitive environment, nepheline syenite plays an important role. Due to its low melting point and melting ability, the use of nepheline syenite in glass and ceramics has been analyzed in many studies conducted since the early 1900s. Its main use is in the glass, ceramic, filler, pigment, paint, coating and roofing granule sectors. Its use for ceramic sanitaryware, tiles, electric porcelains, tableware and glazes is based on its low firing temperatures and fast firing programs [1].
Ball mills have been used in the ceramic sector and in various other industries for close to 100 years, although the basic mechanisms involved in breakage are yet to be fully understood. Early theories of crushing were based on the simple empirical relationship between energy input and size reduction ratio [5, 6]. As no attention was paid to the kinetics of breakage and the sub-processes involved in grinding, the equations applied in these models led to design problems during attempts to increase scales for commercial applications. Thus, the process of grinding, which was not very efficient to begin with, became even less so. To address these problems and to increase grinding efficiency, models based on the kinetics of breakage in mills were developed [7, 8].
Through the advances in mathematical modeling and simulation techniques, significant improvements have been achieved, especially in the optimization of grinding circuits. There have been several studies proposing different approaches to this issue, including Herbst and Fuerstenau (1980), Austin et al. (1982), Kavetsky and Whiten (1982), and Morrell and Man (1997) [9-12]. All of the proposed methods involve laboratory or pilot-scale test data, a ball mill model based on the equivalence of the amount of materials in each size fraction, and different scale-enlargement processes. Methods based on modeling and simulation consider the circuit as a whole, and as such, allow the interaction between the ball mill and other equipment to be identified. This makes it possible to calculate the effect of any changes in the design or operation variables on flow tonnages and particle size distributions.
One of the variable parameters affecting the grinding process in a ball mill is the properties of the grinding balls, such as their shape, size and specific weight. These are the main factors affecting the particle size of the ground product, particle size distribution, grinding cost, energy consumption, capacity and efficiency. To avoid problems during grinding, the shape and size of the grinding ball should be appropriate for the area being used.
Previous studies have examined the grinding behaviors of various raw materials, while to the best of our knowledge there has yet to be any study examining the effects of breakage rate parameters on the technological parameters of ceramic materials [13-23]. Also, in some other studies, the effect of nepheline syenite on ceramic materials is examined [24-27]. The relationship between the technical properties of rocks and their breakage parameters have been ascertained in earlier studies, while the present study certainly offers something new and original, identifying the potential correlation between the specific rates of breakage of raw materials on one hand, and firing shrinkage, water absorption, total porosity and firing strength, on the other, as the most critical technological properties of ceramic materials [28, 29].

The present experimental study made use of nepheline syenite obtained from the Akpınar region of the province of Kırşehir, the specific weight of which was found to be 2.44 g/cm³ [30]. The nepheline syenite was characterized through determination of X-ray fluorescence (XRF) using Spectro equipment, model X-Lab 2000; X-ray diffraction (XRD) using Philips equipment, model X’Pert MPD, with radiation Cu-Kα (45 kV/40 mA).
Table 1 presents the chemical composition of nepheline syenite. The amounts of Fe₂O₃ and MnO in the nepheline syenite were 0.29 and 0.01 mass-%, respectively. Nepheline syenite contains a very small amount of TiO₂.
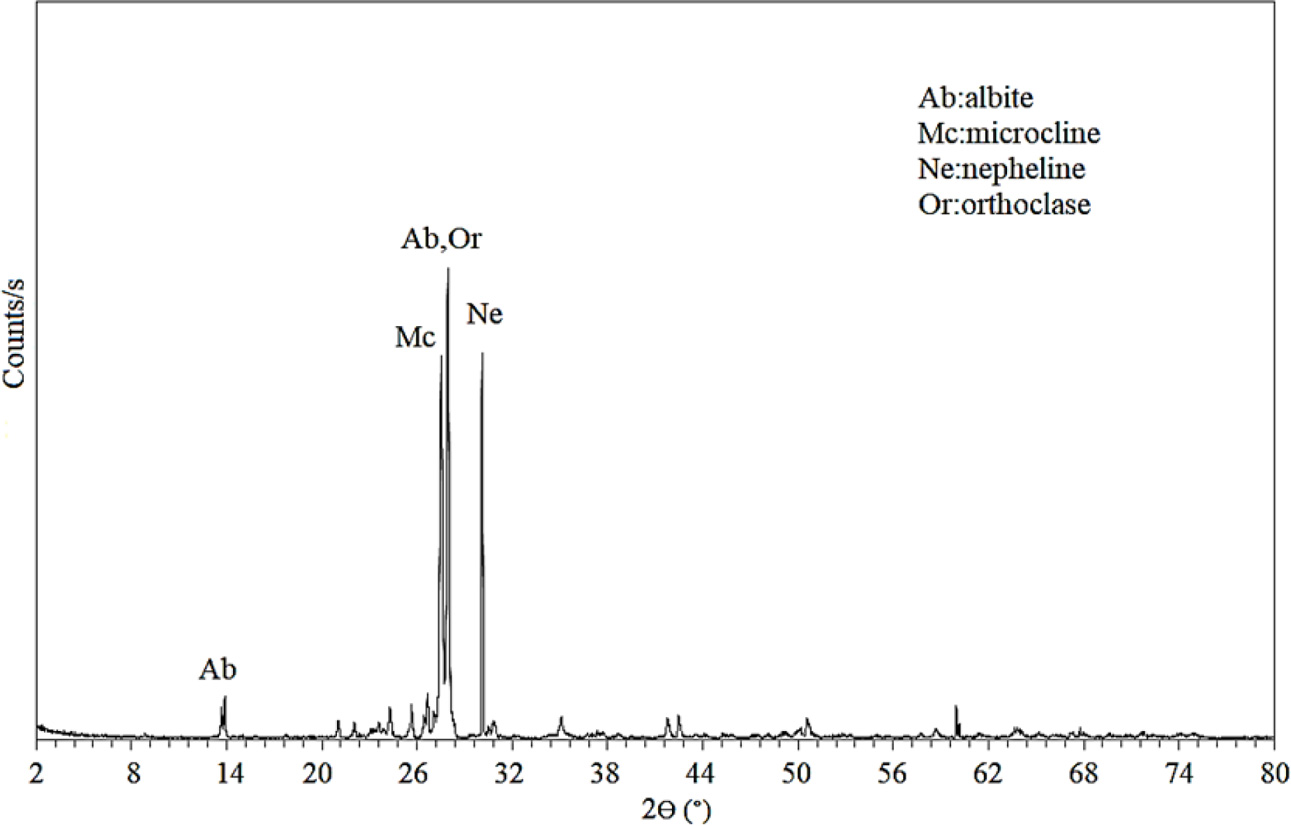
Fig. 1 shows the X-ray diffraction patterns of nepheline syenite. Akpınar nepheline syenite consists of nepheline, orthoclase, albite and microcline. The XRD results were confirmed by XRF.
First, the specific rate of breakage (S_i) of the nepheline syenite to a mono-size fraction was identified, based on the kinetic model developed by Austin, Klimpel and Luckie (1984). Accordingly, the specific rate of breakage of nepheline syenite with a particle size range of -63+53 μm was calculated using Equation (1), while Eqs. (2), (3) and (4) were used, respectively, to calculate the fractional powder filling (f_c = 0.12), the fractional ball filling (J = 0.30) and powder-ball loading ratio (U=1). The mill charge consisted of 1/4, 5/16, 3/8, 1/2 and 3/4 inches alloy steel balls with density ρ_b = 8.09 g/cm³. Experiments were performed in a laboratory-scale ball mill with a volume of 2650 cm³ operating at a constant speed of N = 83-88 rpm (1.38-1.47 Hz), which is 75% of its critical speed.
 

 
Q_i are the correction factors. Q_i=1 for smaller sizes and becomes small for large sizes. X_i, represents the upper size (mm) of the range i. The value of α is a positive number, normally in the range 0.5 to 1.5, which is characteristic of the material (providing the test conditions are in the normal operating range) but the value of a will vary with mill conditions [8].
 

 
In kinetic experiments conducted in dry environments under specified conditions, materials of a mono-size fraction have been ground for linearly increasing grinding periods (0.5, 1, 2, 4, 8, 16, 32, and 64 min). After each grinding period, semi-logarithmic graphs of the material fractions remaining in the top particle size range were plotted against the grinding periods, and the region in which the graph declines linearly is defined as the first-order breakage region. The slope of the line in the first-order breakage region indicates the specific rate of breakage of the material in that particle size range.
The following stage involved the production of the bodies of ceramic materials. Instead of the sodium feldspar found in the standard recipe for ceramic bodies, grinding products from the 64th minute of the kinetic grinding experiment were used. The goal was to investigate the relationship between the specific rates of breakage (S_i) for a given size fraction and the technological properties of the newly developed ceramic bodies, the formula of which is given in Table 2.
The coding for the formulas of the ceramic materials is given in Table 3.
Following the formula in Table 2, the five different ceramic material bodies noted in Table 3 were prepared. For the preparation of the ceramic materials, first, the clay-1 and the silica sand that make up the first phase mixture of the clay were placed in a mill containing porcelain balls, following the formula, and ground for 7.5 h in an aqueous medium. The nepheline syenite was then ground for 64 min (a product of kinetic model experiments) and added to the raw materials, following the formula. In order to obtain a homogeneous sludge, other clays and kaolins were added and mixed for 2 h at 750 rpm in a laboratory mixer. To ensure that clays were completely dissolved, deflocculants (Na₂SiO₃), BaCO₃ and water were added to the mixture in a controlled manner. The preparation of the casting sludge in accordance with the SM1, SM2, SM3, SM4 and SM5 formulas was thus completed. A magnetic separator was used to remove any magnetic impurities from the sludge, and finally, the casting sludge was passed through a 150 μm sieve. To obtain the desired casting qualities, deflocculant (Na₂SiO₃) was added to the sludge until the liter weight, viscosity and thixotropy values were within the appropriate ranges. A liter weight of the sludge was measured using a stainless steel pycnometer (TQC, 100 mL), viscosity was measured using a Brookfield viscometer, and thixotropy was measured using a Torsion viscometer (Gallenkamp type). The particle size measurements of the casting sludge were carried out using a laser particle size analyzer (Malvern, Hydro 2000G). After being kept in the laboratory environment for 24 h, the shaped samples were dried completely in an oven at a temperature of 105±2 ^oC. Dried test rods and tablets were fired in a Riedhammer brand tunnel oven (fueled by natural gas, 110 m long), set at 1,200 ^oC. Eqs. (5), (6) and (7) were used to calculate the firing shrinkage, firing strength and water absorption values, respectively. The total porosity of the fired ceramic bodies was measured using a Poremaster 60 mercury porosimeter (Quantachrome Corporation).
 

 
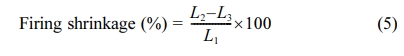
L₁ is the diagonal measurement when the tablet is green, L₂ is the size after drying and L₃ is the size after firing in the oven.
 

 
σ is the breaking strength (kg/cm²), P is the breaking force (kg), L is the distance between supports (cm), b is the the length of the broken surface of the sample (cm) and d is the thickness of the broken region of the sample (cm).
 

 
Water absorption was measured following the TS 800 EN 997 standard. m₀ is the first weight of the fired tablet, while m₁ is the weight of the tablet after removal from the water absorption device.

Breakage rate values of nepheline syenite
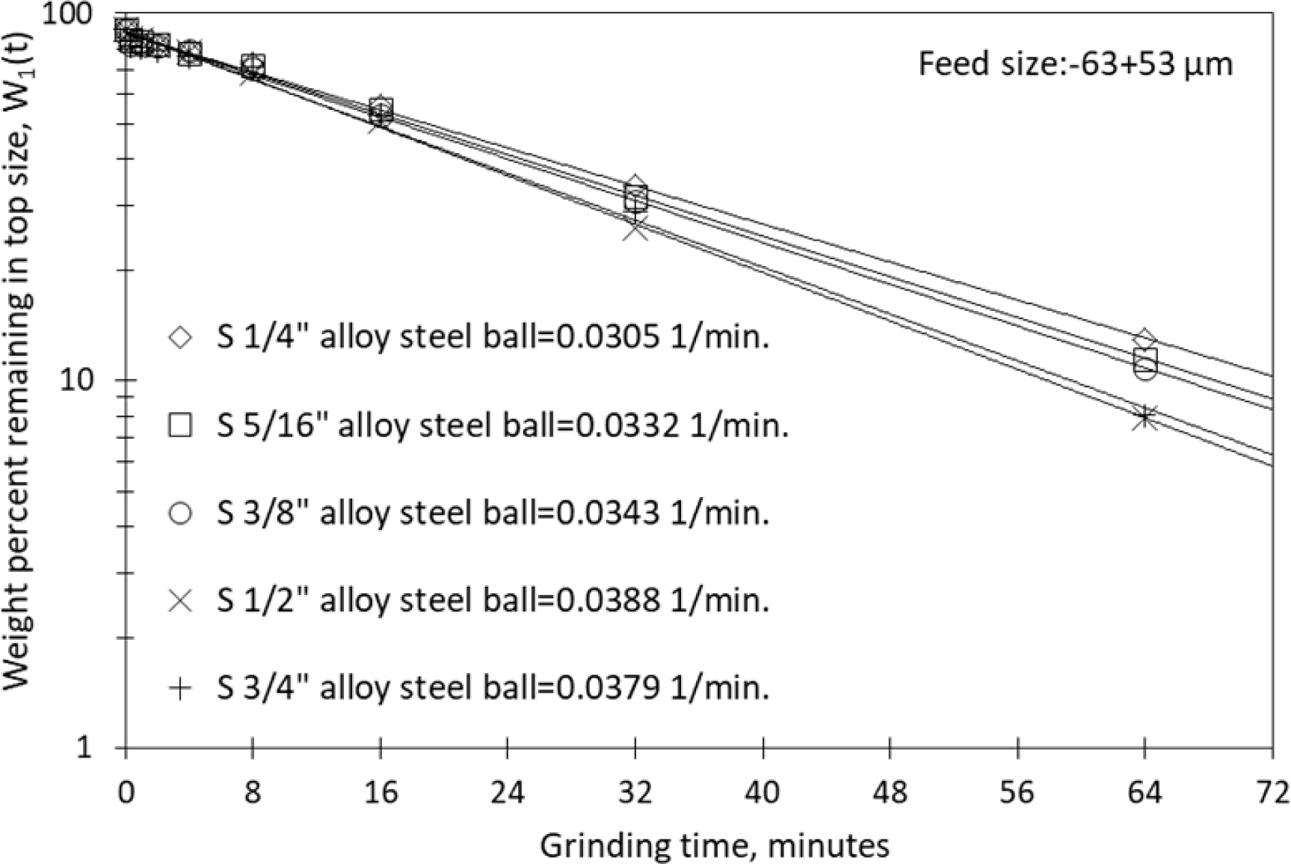
Nepheline syenite of a mono-size fraction was ground for linearly increasing grinding periods using five different ball sizes. After each grinding period, graphs of the material fractions remaining in the top particle size range were plotted against the grinding periods. Fig. 2 reports the first-order breakage kinetics, and Table 4 reports the results.
The d₁₀, d₅₀ and d₉₀ values of the nepheline syenite, after being ground for 64 min, were measured using a laser particle size analyzer (Malvern brand, Hydro 2000G). Multipoint surface areas were measured using a Quantachrome Corporation's Autosorb-6 BET (Brunauer, Emmet and Teller method) device. The results are reported in Table 5.
 
Technological properties of ceramic materials
Table 6 reports the d₁₀, d₅₀, d₉₀, liter weight, viscosity and thixotropy values of the casting sludge of the ceramic materials.
Table 7 presents the technological properties of the ceramic materials fired in a Riedhammer-brand tunnel oven (fueled by natural gas, 110 m long), set at 1,200 ^oC. Of the parameters affecting the technological properties of the ceramic bodies, the body composition, the casting properties and the firing regimes were kept constant in all of the conducted tests. The only parameter that was varied was the particle size distribution of the nepheline syenite samples in the compositions (Table 5).
Table 7 reports the results of the ceramic bodies fired at 1,200 ^oC, in which it can be seen that tablets with larger particle sizes recorded lower firing shrinkage and firing strength values, and higher water absorption values. The firing shrinkage and water absorption values under constant production conditions serve as control parameters in the production of ceramic materials. The firing shrinkage test is the most common approach to controlling the size of ceramic materials. The technological properties of ceramic materials may be related to their firing shrinkage behaviors. The firing shrinkage of ceramic products is, in turn, affected by many factors, including the particle size distributions of the raw materials that make up the composition, their chemical and mineralogical properties and ratios within the sludge, the firing regime of the oven (temperature and time) and the amount of vitreous phase formed during firing. Firing shrinkage takes place as the liquid phase that forms during firing surrounds solid particles fills in the spaces within the body through capillary action [31, 32].
Evaluating Tables 5 and 7 in general terms, lower particle sizes and lower firing temperatures result in greater firing shrinkage values and lower water absorption values for ceramic bodies. The particles that make up the composition were observed to be more reactive when the particle sizes were small. Particle size is the main factor influencing the differences in the firing shrinkage values of bodies with the same body composition that are fired using the same oven regime. Bodies made of clays with fine particle sizes and distributions are considered to have smaller pores, which are easier to remove from the body during firing. This is supported by earlier studies in literature [33-35]. The condensation and shrinkage caused by the liquid phase formation during sintering reduces the number of pores as a result of the rearrangement of particles through capillarity and surface tension effects [32, 36]. Smaller particle sizes increase the reactivity of particles due to the increased surface area, and as a result, the sintering process becomes more efficient (Table 5). Moreover, sintering accelerates with the increase in the number of contact points in cases with smaller particles [37]. Measurements conducted using a mercury porosimeter show that total porosity declines with smaller particle sizes (Table 7). The liquid phase that forms as the particle sizes become smaller creates a highly condensed structure by supporting the reorganization of particles and effective packaging. As porosity declines, the firing shrinkage of the bodies increases. Previous studies in literature have revealed that porosity and density values change depending on the amount of shrinkage that bodies undergo [38, 39]. Moreover, a decline in water absorption is a clear indicator of lower open porosity.
The strength of ceramic materials is defined as the amount of energy required to break the atomic bonds in the material [40]. Tables 5 and 7 show that as particle sizes are decreased, the firing strength of the ceramic bodies increases. At 1,200 ^oC, which is the industrial firing temperature, the firing strength values for SM4 (d₉₀ = 40.937 µm) and SM1 (d₉₀ = 44.043 µm) were 25.67 MPa and 23.44 MPa, respectively, offering a clear indication of the influence of particle size. The rate of dissolution of particles during sintering is inversely proportional to the particle size. During sintering, smaller particles dissolve and disappear, leaving behind only larger particles, which is why strength is affected by the presence of larger particles. Three different hypotheses have been developed regarding the variables affecting the strength of ceramic bodies, being the mullite hypothesis, the matrix reinforcement hypothesis and the strength through dissipative phase hypothesis. The mullite hypothesis was first proposed by Zoellner (1908), and is one of the oldest theories explaining the strength of ceramics. According to the mullite hypothesis, the greater the amount of mullite in the structure, and the higher the strength. Mullite crystals have excellent mechanical, creep resistant, thermal and chemical properties [41]. That said, there have also been studies reporting that, contrary to the mullite hypothesis, no parallel increase in strength values occurs as the amount of mullite in the structure is increased [42-45]. According to the matrix reinforcement hypothesis, the differences between the thermal expansion coefficients of the matrix (the vitreous phase) and the dispersed particles (such as quartz and alumina) or crystalline phases (such as mullite and cristobalite) generate strong compressive stresses. The thermal compressive stress resulting from differences in thermal expansion increase the strength of ceramic bodies. Finally, according to the strength through dissipative phase hypothesis, crystal phases in the vitreous phase of the ceramic body improve strength by limiting the size of cracks [46]. It has been reported in a previous study that strength is unaffected by the amount of mullite phases, and that porosity, microstructural defects and larger particles have a greater effect in this regard [47]. Tables 5 and 7 indicate that larger particle sizes are associated with higher water absorption and lower firing shrinkage values, and consequently, with lower strength values. One of the leading parameters affecting the breaking strength of bodies is the porosity of their microstructures. Tables 5 and 7 show that pores and coarse particles left in the microstructure facilitate the formation of cracks, and thus have a negative effect on breaking strength. Lower porosity and higher density are associated with higher strength in ceramic materials. Theoretically, it would be possible to maximize breaking strength by eliminating all of the pores in the microstructure [43, 45, 48-50]. The findings of both previous studies and the present study reveal the breaking strength of ceramic bodies to be affected by the number, shape and size of the pores in the microstructure of the body. The total porosity and firing strength values reported in Table 7 show that bodies with finer particle sizes have lower total porosity values. At 1,200 ^oC, which is the industrial firing temperature, the total porosity values for SM4 (d₉₀ = 40.937 µm) and SM1 (d₉₀ = 44.043 µm) were 1.3061% and 5.8582%, respectively. This indicates larger particle sizes led to a decreased vitrification rate and an increase in porosity, and as a result, firing strength declined. Stress is concentrated in the pores in brittle ceramic materials. When the stress in the pores reaches a critical value, the formation of cracks begins and progresses. As there is no process to absorb energy throughout the deformation, the crack propagation continues until a break occurs [51].
 
Correlation between ceramic material properties, specific rate of breakage and particle diameter
Using the concept of a linear curve and a simple regression analysis in Excel, an estimating equation is developed between the S_i (Table 4) and d₉₀ values (Table 5) of the nepheline syenite, and the firing shrinkage, water absorption, total porosity and firing strength values (Table 7) of the ceramic materials. 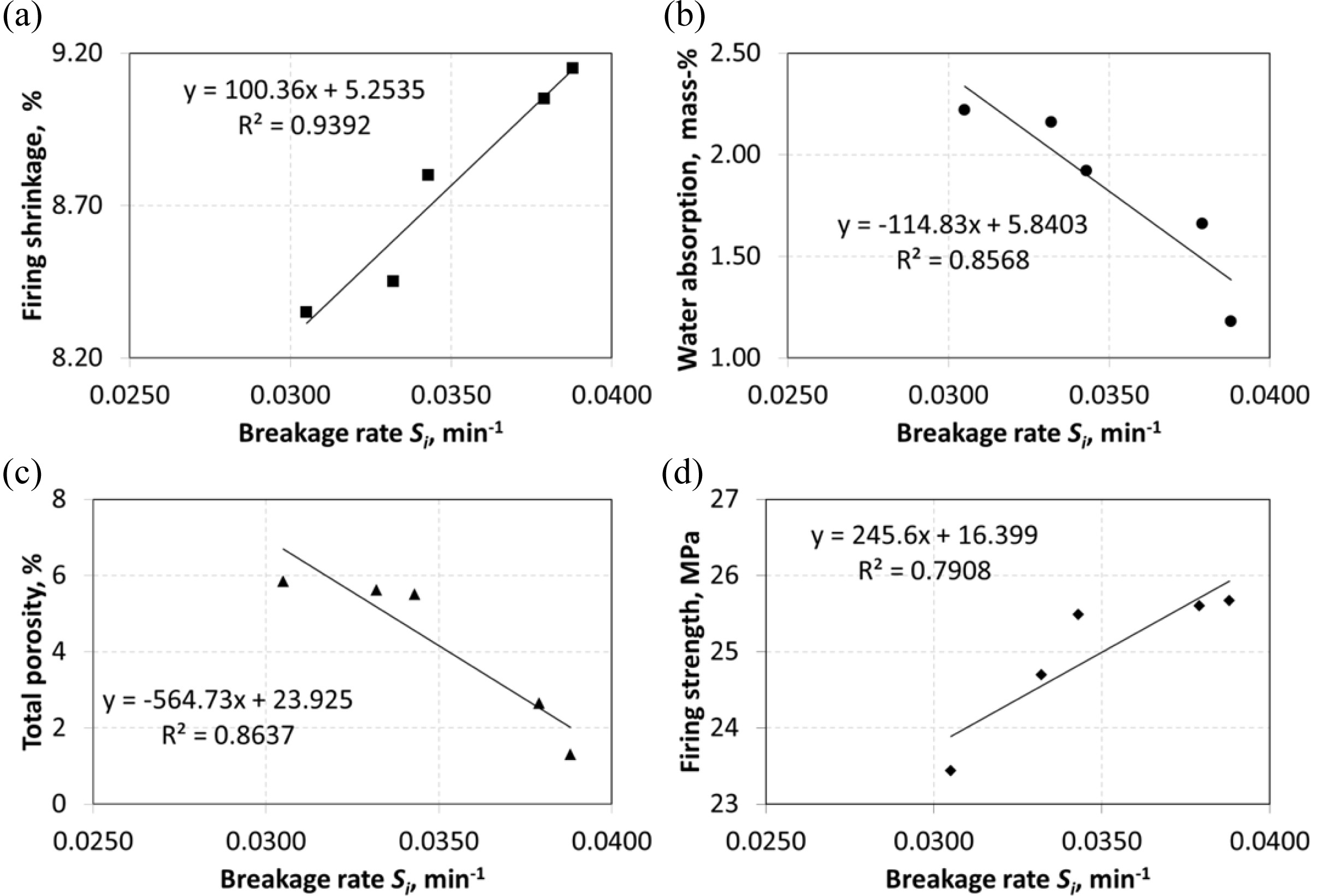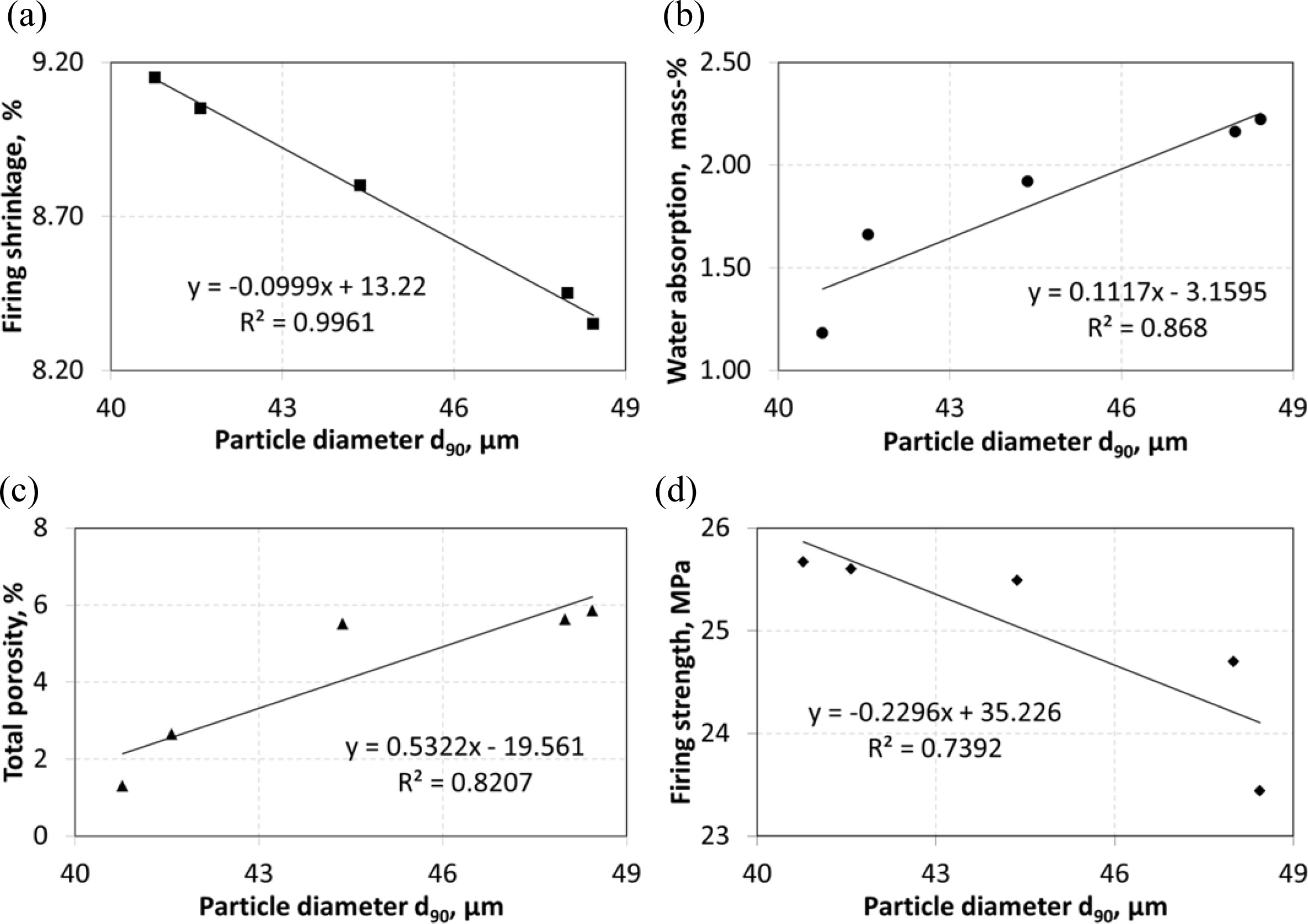The correlations between the S_i and d₉₀ values on the one hand, and firing shrinkage, water absorption, total porosity and firing strength on the other, are reported, respectively, in Figs. 3 and 4.
Graphs (a), (b), (c) and (d) in Fig. 3 show a linear relationship. It is seen that very strong correlation between S_i and firing shrinkage (R²=0.9392) and strong correlations between S_i and water absorption (R²=0.8568), total porosity (R²=0.8637) ve firing strength (R²=0.7908).
Graphs (a), (b), (c) and (d) in Fig. 4 show a linear relationship. It is seen that very strong correlation between d₉₀ and firing shrinkage (R²=0.9961) and strong correlations between d₉₀ and water absorption (R²=0.8680), total porosity (R²=0.8207) ve firing strength (R²=0.7392).
When materials are ground in the mill, the sizes of products and the rate at which they are produced are an outcome of the size-mass balance. Different rates of breakage are observed within the mill, depending on the particle size. S_i represents the specific rate of breakage of the particles in a given size range “i”, and the unit of the specific rate of breakage is time^-1. In other words, the S_i value of materials classified in a mono-size range is determined through a particle size analysis conducted at the end of each grinding period. In order to control such technological properties of ceramic materials as firing shrinkage, water absorption, total porosity and firing strength, it is important to identify the particle sizes and particle size distributions of the raw materials used. The particle size and the degree of particle size distribution affect the reactivity of the components in the composition during firing, and thus the number of of new phases (vitreous and crystal) to be formed. Literature contains many studies on this topic [45, 52-54]. It is thus particle size that underlies the relationship between the technological properties of ceramic materials and the specific rate of breakage of the non-plastic materials used in ceramic materials (Table 5). Looking at the relationships between the S_i and d₉₀ values of non-plastic materials and firing shrinkage, water absorption, total porosity and firing strength, which are among the technological properties of ceramic materials (Fig. 3 and 4), coefficients of determination (R²), are observed to vary between 0.9961 and 0.7392. These results indicate strong or very strong relationships between the S_i and d₉₀ values of the nepheline syenite used in ceramic materials and the technological properties of ceramic bodies.
It is not always possible to explain a dependent variable with a single independent variable. Variations in the technological properties of ceramic materials are usually a result of multiple factors, and a large number of variables may come together to produce an effect on another variable. Furthermore, these variables may also have interactive effects on each other. For this reason, in this study, to identify correlations between two independent variables, which are S_i values (Table 4) and d₉₀ values (Table 5) of nepheline syenite, and firing shrinkage, water absorption, total porosity and firing strenght of ceramic materials (Table 7) multiple regression analysis was performed by using excel software. The correlation matrix for d₉₀, S_i, firing shrinkage, water absorption, total porosity and firing strenght is shown in Table 8.
 


According to the results of multiple regression analysis, for each dependent variable the two independent variables with the highest correlation coefficients, as shown in the correlation matrix, were used to perform the analysis. The firing strength of ceramic materials may be influenced by variables other than firing shrinkage, water absorption, porosity and particle size. Changes in firing strength should be evaluated on the basis of mullite, matrix reinforcement and strength through the dissipative phase hypotheses discussed in previous parts. For the reasons explained here, it was expected that the correlation coefficients between firing strength and the independent variables would be slightly lower. Table 8 shows that high correlation coefficients were obtained between firing strength and independent variables.

In the first stage of this study, 1/4, 5/16, 3/8, 1/2 and 3/4 inches alloy steel balls were used to identify changes in the specific rate of breakage of the nepheline syenite in a particle size range of -63+53 μm, as a non-plastic raw material used as an alternative melter for ceramic materials. All mill parameters aside from ball size were kept constant. Products obtained after 64 minutes of grinding using these five different ball sizes were added to the ceramic material composition as an alternative to sodium feldspar. In the final stage, correlations between specific rates of breakage of non-plastic raw material (S_i) and the technological properties (water absorption, firing shrinkage, total porosity and firing strength) of ceramic materials were examined.
The S_i values obtained from experiments conducted using 1/4, 5/16, 3/8, 1/2 and 3/4 inches alloy steel balls showed effective breaking until the ball size of 1/2 inches was reached, as the original particles were quickly reduced to smaller sizes.
The d₉₀ particle sizes of the sludge were reduced with the addition of grinding products to the composition of the ceramic materials, and this seemed to result in further condensation in the fired bodies. As a result, the bodies’ firing shrinkage and condensation values were higher, and water absorption and porosity values were lower, and higher breaking strength values were obtained for bodies with smaller particle sizes.
The relationship between the specific rate of breakage of nepheline syenite and the technological properties of the ceramic products is related to the particle size in the melting phase in the structure of ceramic materials.

The author would like to acknowledge the TUBITAK for financially supporting this study (project name: TUBITAK-MAG-118M224).