Fly ash is an industry by-product of thermal power factories that is broadly utilized in the concrete industry. This research shows a framework for evaluating the hydration heat, reaction amount, and strength progress of cement–fly ash binary composite. First, we conducted an experiment to study the isothermal hydration heat of fly ash composite paste with assorted fly ash contents and temperatures. According to the experimental outcomes of cumulative hydration heat, the coefficients of a kinetic reaction model of fly ash were determined. Furthermore, the reaction amount of fly ash was calculated using a fly ash reaction model. We discovered that the reaction of fly ash is considerably improved at elevated temperatures. The reaction amount of fly ash decreases with the growing content of fly ash. Second, in line with the reaction amount of fly ash and cement, we developed a straight-line equation for evaluating the strength progress of binary composite. The strength progress model applies to a number of water-to-binder ratios and fly ash substitution ratios. Summarily, the suggested hydration–heat–strength model is helpful for understanding the material style of fly ash concrete.

Keywords: Fly ash, Hydration heat, Reaction degree, Strength, Model

Fly ash is really a pozzolanic mineral admixture that is able to interact with calcium hydroxide to create secondary calcium silicate hydrate. Fly ash concrete shows several benefits, for example, low hydration heat and low temperature increase of hardening concrete, good workability, high long-term strength, and high resistance of chloride ingression. Evaluations of qualities, for example, hydration heat and strength development, are useful for the rational usage of fly ash in construction [1, 2].
Many numerical models have been proposed for binary composite containing fly ash and cement. Lam et al. measured the amount of reaction of fly ash using the technique of selective dissolution and evaluated the progress of strength of binary composite using gel–space ratios [3]. Schindler and Folliard predicted the hydration heat of hardening concrete with supplementary cementing materials, for example, slag and fly ash. Furthermore, an overall reaction degree of binders was proposed in Schindler and Folliard’s study [4]. Based on the experimental results of calcium hydroxide content, Pane and Hansen analyzed the amount of reaction of mineral admixtures, for example, slag, fly ash, and silica fume [5]. Based on isothermal hydration heat, Han et al. analyzed the kinetic hydration process of fly ash composite paste,  and an overall reaction degree was used for binary composite[6]. Baert et al. proposed a multi-component model for evaluating the release of hydration heat of blended paste with various fly ash contents [7]. Nath et al. analyzed the kinetic reaction of fly ash geopolymer using isothermal hydration heat and the modified Jander equation [8]. Deschner et al. proposed thermodynamic modeling for fly ash composite concrete, in which the phase assemblage of binary composite at various curing temperatures is evaluated [9]. Xu et al. evaluated the hydration heat and amount of reaction of binary composite using a three-parameter equation [10]. Narmluk and Nawa proposed a theoretical model of hydration and calculated the reaction amount of cement in composite paste containing fly ash and cement, and the improvement of the amount of reaction of cement because of the addition of fly ash addition was clarified [11]. Garcia-Lodeiro et al. proposed a descriptive model for the reaction of binary composite containing alkalis [12], and the effects of different types of alkalis on hydration products were clarified [12].
Although many modeling investigations have been proposed for fly ash concrete, these investigations show some weak points. First, most of the studies focus on single properties of concrete, such as hydration heat [4, 6-8, 10] or strength development [3]. To rationally use fly ash, an integrated model for both hydration heat and strength development will be more helpful for engineering practices. Second, in previous studies [5, 8, 10], the parameters of the models are dependent on a specific mix of ratios, such as the water-to-binder ratio and the fly ash substitution ratio. When the mixtures are changed, it is difficult to use these models [5, 8, 10]. Third, most hydration models focus on ordinary-strength or high-strength concrete [4-7, 9-11], which has a water-to-binder ratio higher than 0.3. Studies on the hydration of cement-based materials that have a much lower water-to-binder ratio are very limited. On the other hand, ultra-high-performance concrete that has a very low water-to-binder ratio is increasingly being used in constructions [13, 14]. Thus, it is necessary for us to propose a new hydration model that is valid for ultra-high-strength, high-strength, and ordinary-strength concretes.
To overcome the flaws of previous studies, this research proposes a framework for evaluating the release of hydration heat, reaction amount, and strength progress of binary composite. According to the experimental outcomes of isothermal hydration heat with assorted temperatures, the reaction amount of fly ash is calculated using a kinetic reaction model. Furthermore, in line with the reaction amount of fly ash and cement, a straight-line equation is suggested for evaluating the strength progress of binary composite with assorted water-to-binder ratio and fly ash-to-binder ratio. The suggested hydration–heat–strength model is helpful for understanding the material style of fly ash concrete.

The cement hydration model
Our previous study showed a model for the kinetic hydration process of Portland cement [13, 15]. This model takes into account the kinetic phases of hydration, for example, the phases of initial dormant, boundary reaction, and diffusion. The degree of hydration of cement a can be calculated using a method of integration such as a = , where da/dt is the rate of hydration of cement. The model of cement hydration considers the shortage of capillary water and, consequently, the insufficient hydration of concrete with a low water-to-binder ratio, such as high-strength and ultra-high-strength concretes. The input parameters of the hydration model consist of cement compositions, concrete mix ratios, and curing circumstances. The output result of the hydration model is the reaction amount of cement.
 
The fly ash reaction model
Fly ash is a type of pozzolanic material that can react with calcium hydroxide and can form secondary calcium silicate hydrate [16]. Compared to cement, the reactivity of fly ash is low. The initial dormant period of the reaction of fly ash is long. In addition, the kinetic reaction process of binary composite is similar to that of plain cement [17]. At a late age of hydration, the control stage of pozzolanic reaction is diffusion [18]. Considering the material characteristics and reaction kinetics of fly ash, we assume the reaction of fly ash comprises the phases of initial dormant, boundary reaction, and diffusion. The kinetic reaction equation process is shown as follows:
 

 
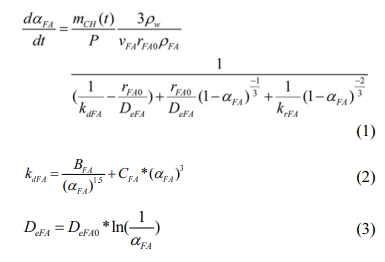
where a_FA denotes the reaction amount of fly ash; m_CH(t) and P denote the masses of calcium hydroxide in hydrating binary composite and fly ash in the concrete, respectively; n_FA denotes the stoichiometric ratio of fly ash to calcium hydroxide (n_FA = 0.845 -0.7(P/(C+P)), where C denotes the mass of cement in concrete [13]); r_FA0 denotes the average radius of the particles of the fly ash; r_FA and r_W denote the density of the fly ash and water, respectively; k_dFA denotes the reaction rate coefficient of the dormant stage (B_FA and C_FA are sub-coefficients); D_eFA0 denotes the initial diffusion coefficient of the diffusion stage; and k_rFA denotes the reaction rate coefficient of the boundary reaction stage.
For binary composite, calcium hydroxide content is dependent on both the hydration of cement and the reaction of fly ash. The mass of calcium hydroxide can be established as follows:
 

 
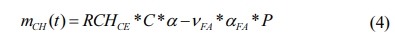
where RCH_CE is the calcium hydroxide production when the unit mass of cement hydrates; a is the hydration degree of cement; and RCH_CE * C * a and n_FA * a_FA * P denote the calcium hydroxide production from the hydration of cement and from the reaction of fly ash, respectively.
For binary composite, capillary water is consumed by the reactions of fly ash and cement. The content of capillary water can be determined as follows:
 

 
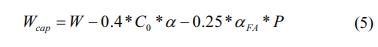
where W_cap and W are the masses of the remaining capillary water and mixed water in concrete mixtures, respectively; and 0.25 * a_FA * P and 0.4 * C * a refer to the masses of consumed capillary water from the reaction of fly ash and from the hydration of cement, respectively.
Fly ash reaction is sensitive to temperature. When curing temperature increases, fly ash reaction accelerates. To consider the influence of temperature on the reaction of fly ash, we used the Arrhenius law as follows:
 

 
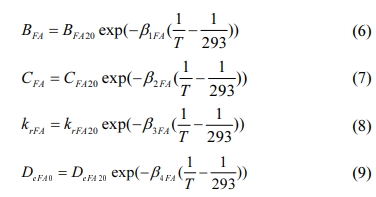
where B_FA20, C_FA20, D_eFA20, and k_rFA20 denote the values of coefficients B_FA, C_FA, D_eFA0, and k_rFA at 293 K, respectively; and b_1FA, b_2FA, b_3FA, and b_4FA denote the temperature sensitivity coefficients of B_FA, C_FA, k_rFA0, and D_eFA0, respectively. Based on the reaction quantity of fly ash at various curing temperatures, the temperature sensitivity coefficients b_1FA, b_2FA, b_3FA, and b_4FA can be discovered.
For binary composite, fly ash reaction and cement hydration play a role in the hydration heat. The discharge of hydrate heat is proportional to the amount of hydration. The entire hydration heat is the sum of the reaction of fly ash and the hydration of cement. The hydration heat of binary composite can be established as follows:
 

 
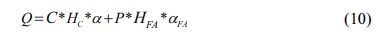
where Q is rate of heat generation; H_C and H_FA denote of heat generation for cement and fly ash, respectively, where H_C can be determined from cement compound compositions and H_FA is equal to 50 kcal/kg [19]; and P * H_FA * a_FA and C * H_C * a denote the release of heat from the reaction of fly ash and from the hydration of cement, respectively.
 
The strength development model
Compressive strength can be a basic property of cement-based materials. The construction process and structural design closely relate to the development of concrete strength. The strength of concrete is linearly based on the reaction quantity of cement [20]. Con-       sidering both the pozzolanic property of fly ash and the hydration process of cement, the development of the strength of binary composite can be discovered by:
 
 

 

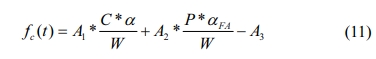
where f_c refers to the concrete strength; A₁, A₂, and  A₃ are the coefficients of strength; A*((C*a)/W) considers the influence of cement hydration on strength; A₂*((P*a_FA)/W) considers the influence of fly ash hydration on strength; and A₃ considers the concrete strength starts after a threshold time, not after the mixing time. The coefficients A₁, A₂, and A₃ can be determined according to experimental outcomes of the strength of concrete. Because the reaction amounts of binders a and a_FA are dependent on time, the strength of concrete is a function of time.

The hydration heat model
As proven in eq. (10), the discharge of the hydration heat of binary composite pertains to both cement and fly ash. To look for the reaction coefficient of fly ash, we conducted experiments on isothermal hydration heat with elevated temperatures and fly ash contents. The water-to-binder ratio of the paste specimen was 0.5; the fly ash substitute ratio was 0%, 20%, or 40%; and the temperatures were set as 20, 35, or 50 ^oC. 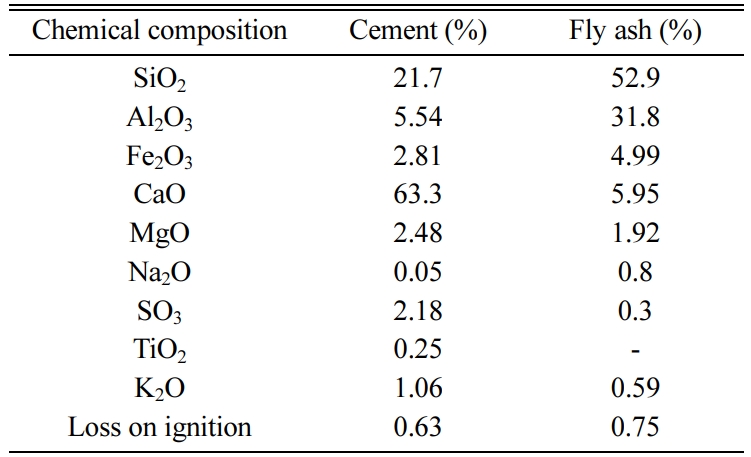The chemical compositions of fly ash and cement are given in Table 1. The paste was mixed utilizing a mechanical agitator and 5 g of paste was taken for the measurement of hydration heat. The development of hydration heat was measured by using TAM-air, and the duration of the hydration heat measurement was 72 h [21, 22].
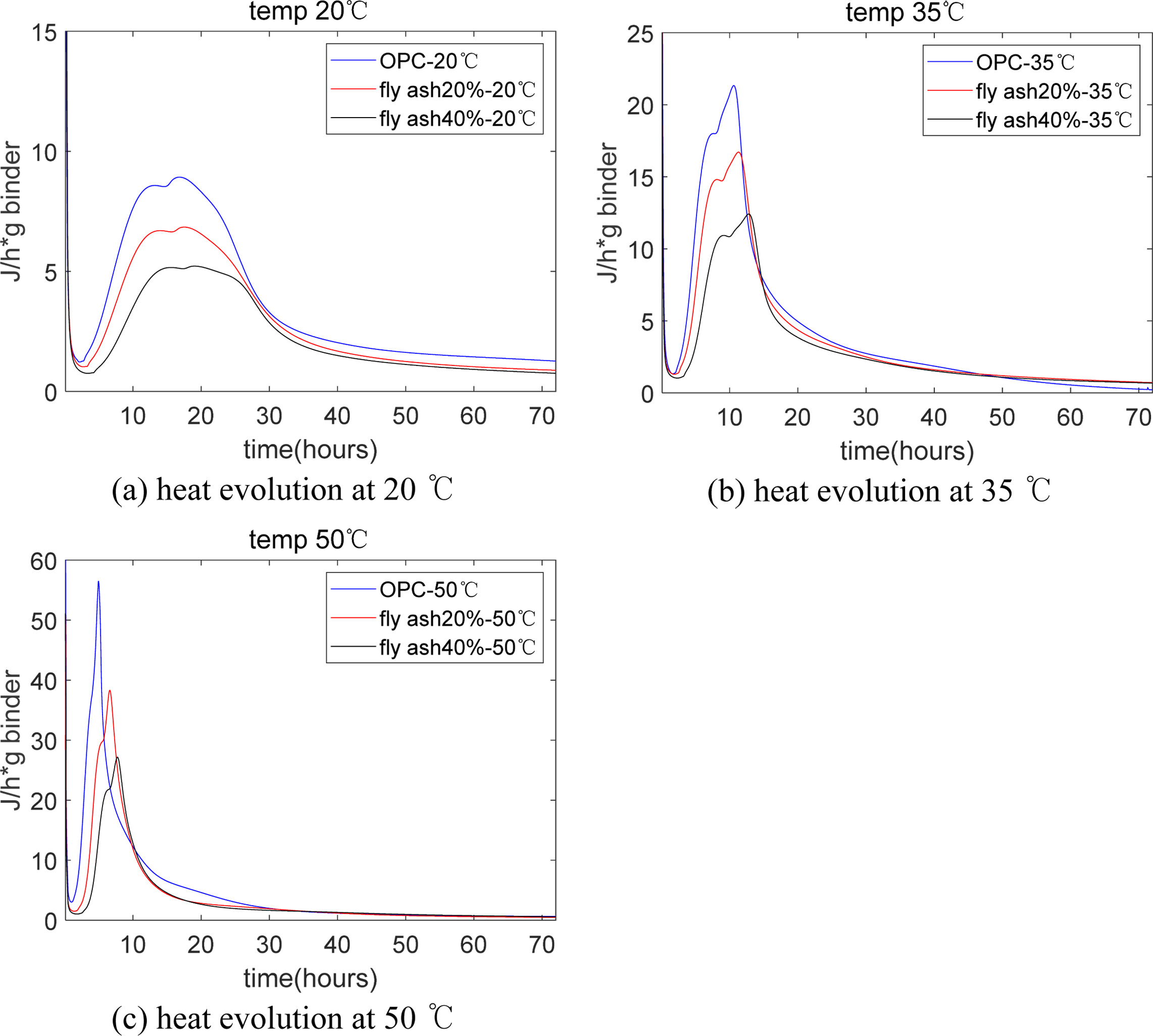
The experimental outcomes of the rate of hydration heat are shown in Fig. 1. First, Fig. 1(a) shows for plain paste at 20 ^oC, the main exothermic peak occurs at about 10 h. This exothermic peak is due to the hydration of alite. At the deceleration stage, the exothermic peak may be from the renewed dissolution of C₃A [21, 22]. As the temperature increases from 20 ^oC to 50 ^oC (from Fig. 1(a) to 1(c)), the main exothermic peak occurs much earlier, and the value of the exothermic peak also increases. Second, for binary composite, with increasing contents of fly ash, the hydration heat decreases. This is from the dilution effect of the addition of fly ash. In addition, for specimens with fly ash, the occurrence time of the exothermic peak slightly retards. This can be due to the fact that the reactivity of fly ash is gloomier than cement, and the hydration heat of binary composite is lower than plain cement. Third, Fig. 1(c) shows at 50 ^oC, for Portland cement, the exothermic peaks of C₃S reaction and C₃A renewed dissolution merge together. Meanwhile, for binary composite, at the deceleration stage, the exothermic peak may be from the reaction of fly ash.
The reactivity of fly ash is low at normal temperatures, such as 20 ^oC, and also the growing temperature can accelerate the reaction of fly ash and can increase of heat release of binary composites [21, 22]. However, we ought to observe that the hydration heat is not the direct measurement of the reaction amount of fly ash. To calculate the reaction amount of fly ash, the regression of the reaction coefficients of the blended hydration model is essential. Within this study, experimental outcomes of cumulative hydration heat can be used for regression of the coefficients of the blended hydration model.
As proven in eq. (10), hydration heat pertains to fly ash reaction and cement hydration. The hydration heat of cement can be calculated using the Portland cement hydration model within our previous study [15, 21]. Furthermore, the coefficients of fly ash can be established according to the experimental outcomes of the binary composite. The reaction coefficients of fly ash are shown in Table 2. When the mixtures of concrete change, the reaction coefficients do not change.
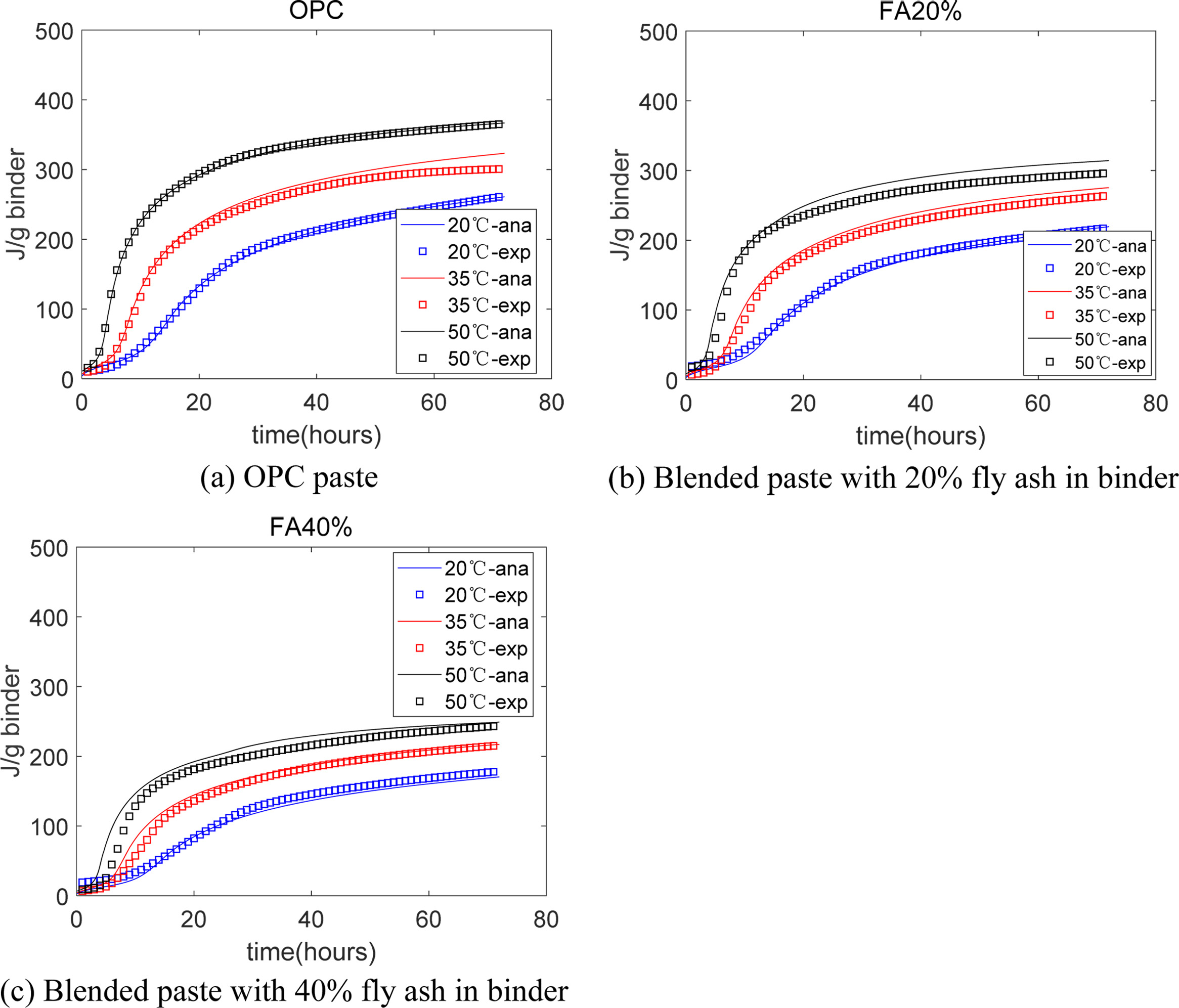
The calculation results of cumulative hydration heat are shown in Fig. 2. Fig. 2(a) to 2(c) show in the early age, the accumulative hydration heat rapidly increases, and at late ages, the increase in hydration heat is not obvious, especially for specimens with a high temperature of 50 ^oC. This is because at the late age, diffusion is the control stage, and the hydration of the binder is accelerated at elevated temperatures. Generally, the evaluation results show agreement with the experimental outcomes. From Fig. 2(a) to 2(c), with an increasing fly ash substitution ratio, the cumulative hydration heat becomes lower. This is because the reaction heat per mass and reactivity of fly ash are less than that of cement.
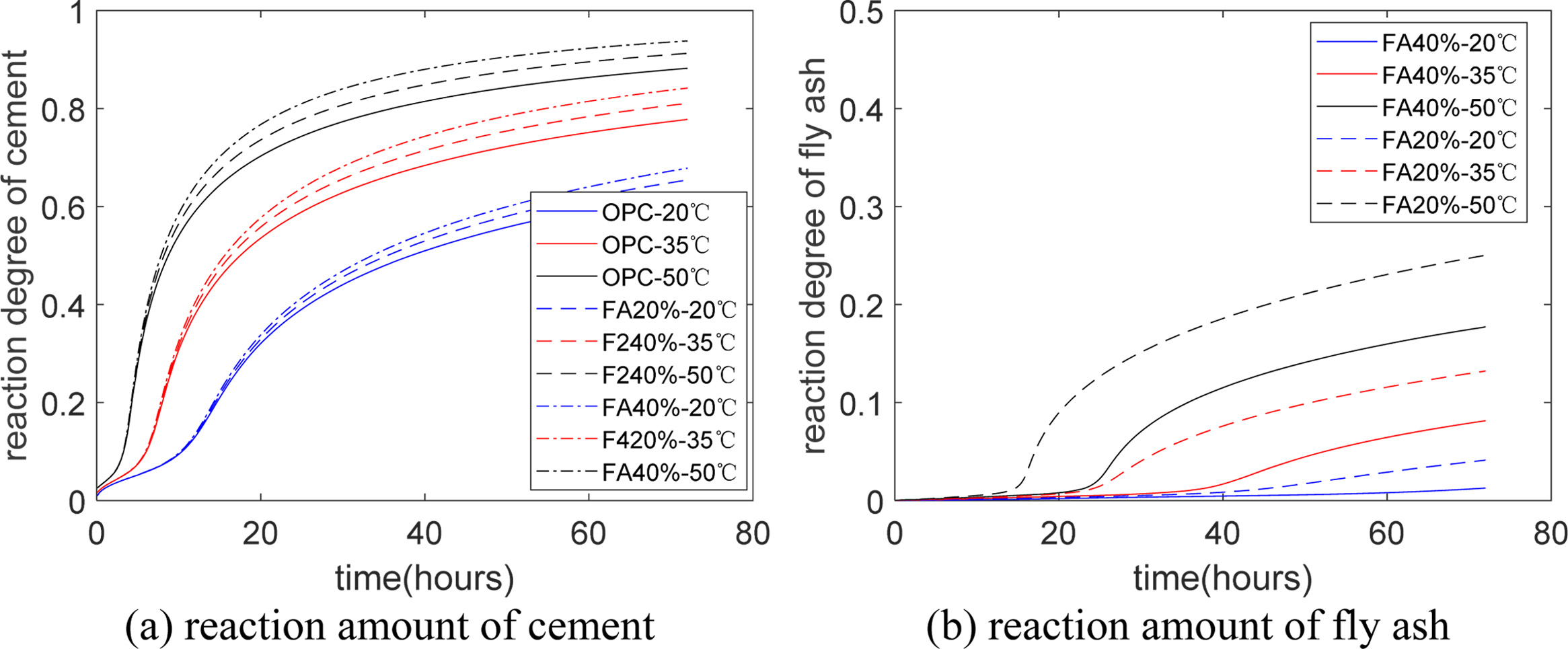
Fig. 3 shows the reaction amount of cement and fly ash. As proven in Fig. 3(a), given a particular temperature, the hydration amount of cement in binary composite is greater than that in plain cement. This is because of the dilution aftereffect of fly ash; after the inclusion of fly ash, the water-to-cement ratio increases, and the rate of hydration of cement increases correspondingly. As proven in Fig. 3(b), using the growing fly ash substitute ratio, the activation aftereffect of calcium hydroxide becomes weaker, and also the reaction amount of fly ash decreases [23]. The reaction amount of fly ash is a lot less than cement. Especially at 20 ^oC, the reaction amount of fly ash is under 5%. At elevated temperatures, the reaction amount of fly ash clearly increases [24]. Quite simply, isothermal calorimetry with high tem peratures may be used for indirectly identifying the reaction amount of fly ash.
Within this study, the reaction amount of fly ash was determined using hydration heat. However, there are more experimental means of measuring the reaction amount of fly ash, for example, the method of selective dissolution or image analysis. Lam et al. determined the reaction amount of fly ash using the selective dissolution method [3], in which the water-to-binder ratio varied from 0.19 to 0.50, the fly ash substitute ratio varied from 0.25 to 0.55, and the testing ages varied from 7 days to 3 months. The curing temperature of the paste specimen was 27 ^oC [3].
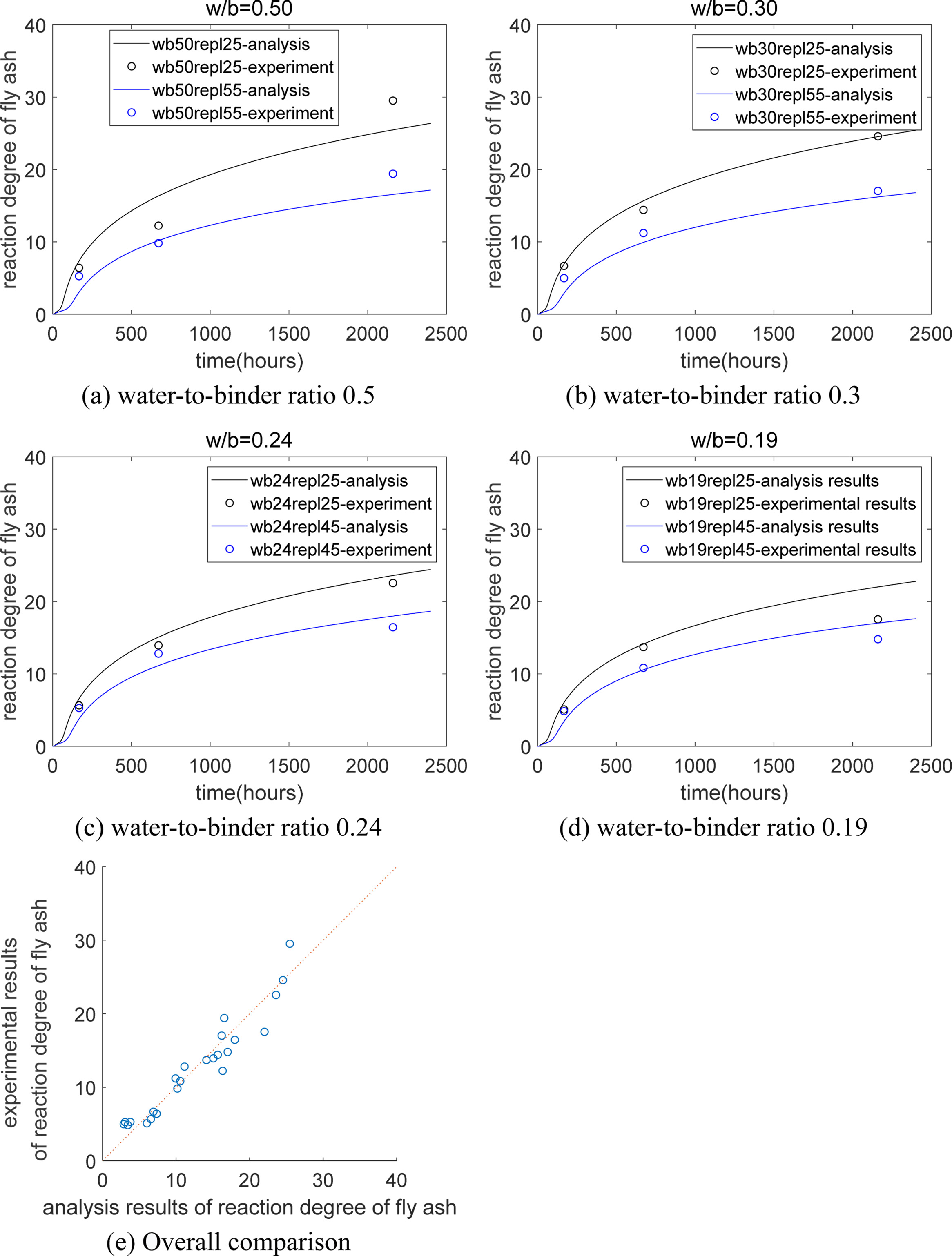
According to the blended hydration model, the reaction amount of fly ash was calculated. As proven in Fig. 4(a) to 4(d), given a particular water-to-binder ratio, the reaction amount of fly ash decreases as fly ash-to-binder ratio increases [25]. This trend is comparable with that in Fig. 3(b). Additionally, given a particular fly ash content, the reaction amount of fly ash decreases as the water-to-binder ratio decreases. This is because the accessible deposit space for hydration products becomes inadequate for concrete that has a low water-to-binder ratio [26]. Fig. 4(e) shows that analysis outcomes generally accept experimental outcomes. The correlation coefficients between the analysis outcomes and the experimental answers are 0.97. Summarily, the suggested blended hydration model is applicable for a number of ages, for example, early-age hydration (isothermal hydration heat) and lengthy-term hydration (reaction amount at 3 months), and it is valid for concrete with assorted water-to-binder ratio and fly ash contents. Since the interactions between the hydration procedure for cement and the reaction procedure for fly ash are taken into consideration with the items in capillary water and calcium hydroxide, the coefficients of the binary composite hydration model do not change for a number of mixtures.
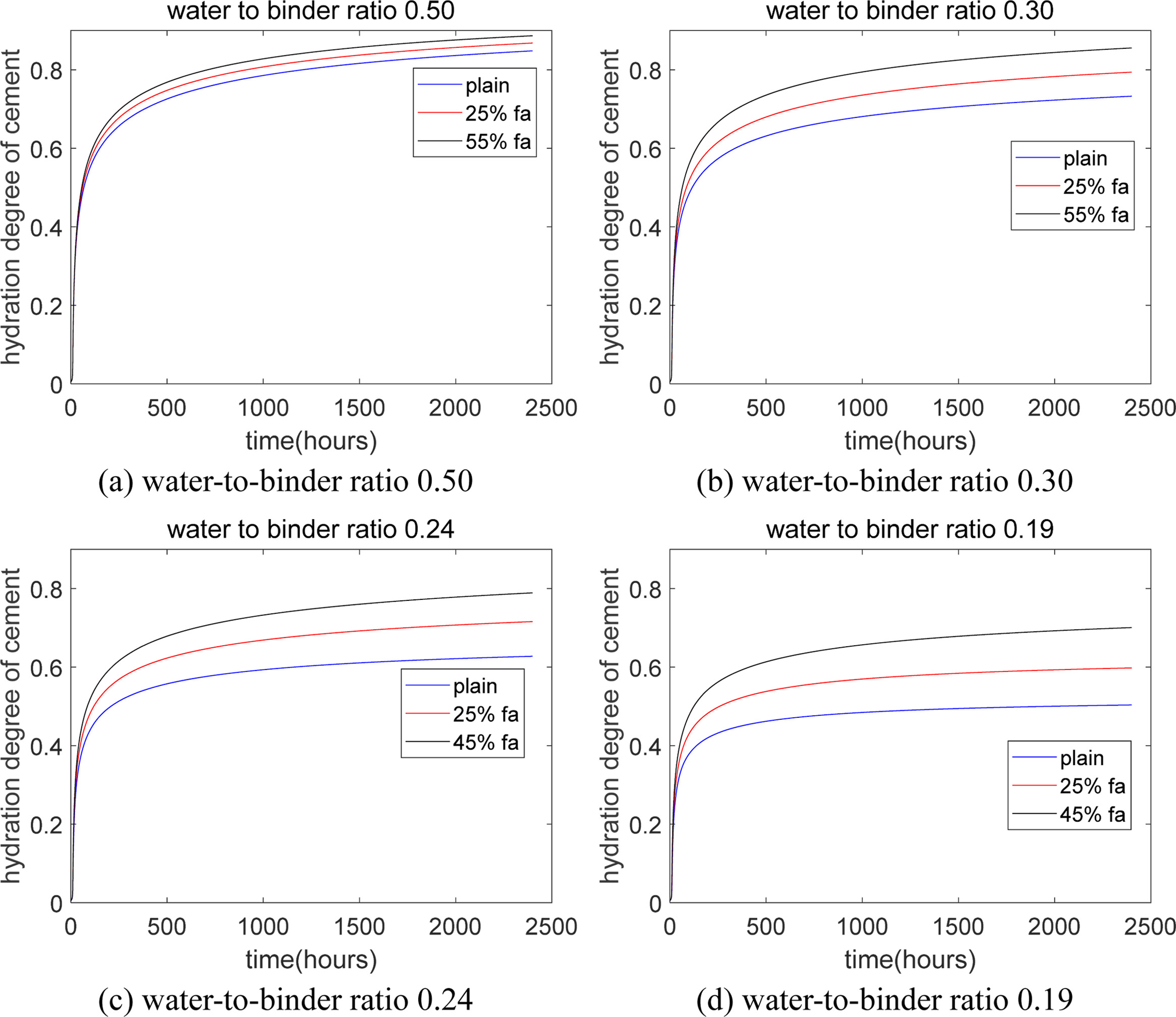
Fig. 5 shows the dilution aftereffect of the addition of fly ash. Given the same fly ash substitute ratio, for examples with low water-to-binder ratio, the advance in the water-to-cement ratio is a lot more significant than that with high water-to-binder ratio. First, Fig. 5(a) shows for a paste that has a high water-to-binder ratio 0.5, the dilution effect is not significant; thus, the advance in the hydration amount of cement is not apparent. In addition, the water-to -binder ratios of Fig. 5(b) and 5c are 0.30 and 0.24, respectively. Compared with Fig. 5(a), the dilution effect shown in Fig. 5(b) and Fig. 5(c) is more obvious. This is due to the reduction of water-to-binder ratio from Fig. 5(a) to Fig. 5(b) and Fig. 5(c). Second, Fig. 5(d) shows for a paste that has a much lower water-to-binder ratio 0.19, because of the dilution aftereffect of the addition of fly ash, the advance in the hydration amount of cement is more apparent than Fig. 5(a), Fig. 5(b), and Fig. 5(c).
 
The strength progress model
As shown in eq. (11), the reaction amounts of binders can be used for evaluating the strength progress of concrete. Lam et al. measured the strength progress of binary composite paste [3]. The mixture of paste specimens for the strength test was the same as those for the reaction degree test. According to the experimental outcomes of strength, the strength coefficients A₁, A₂, and A₃ of eq. (11) were determined as 57.4, 123.1, and -36.2, respectively. The strength coefficient of fly ash A₂ was much higher than coefficient of cement A₁. This is because the SiO₂ content of fly ash is a lot greater than that of cement.
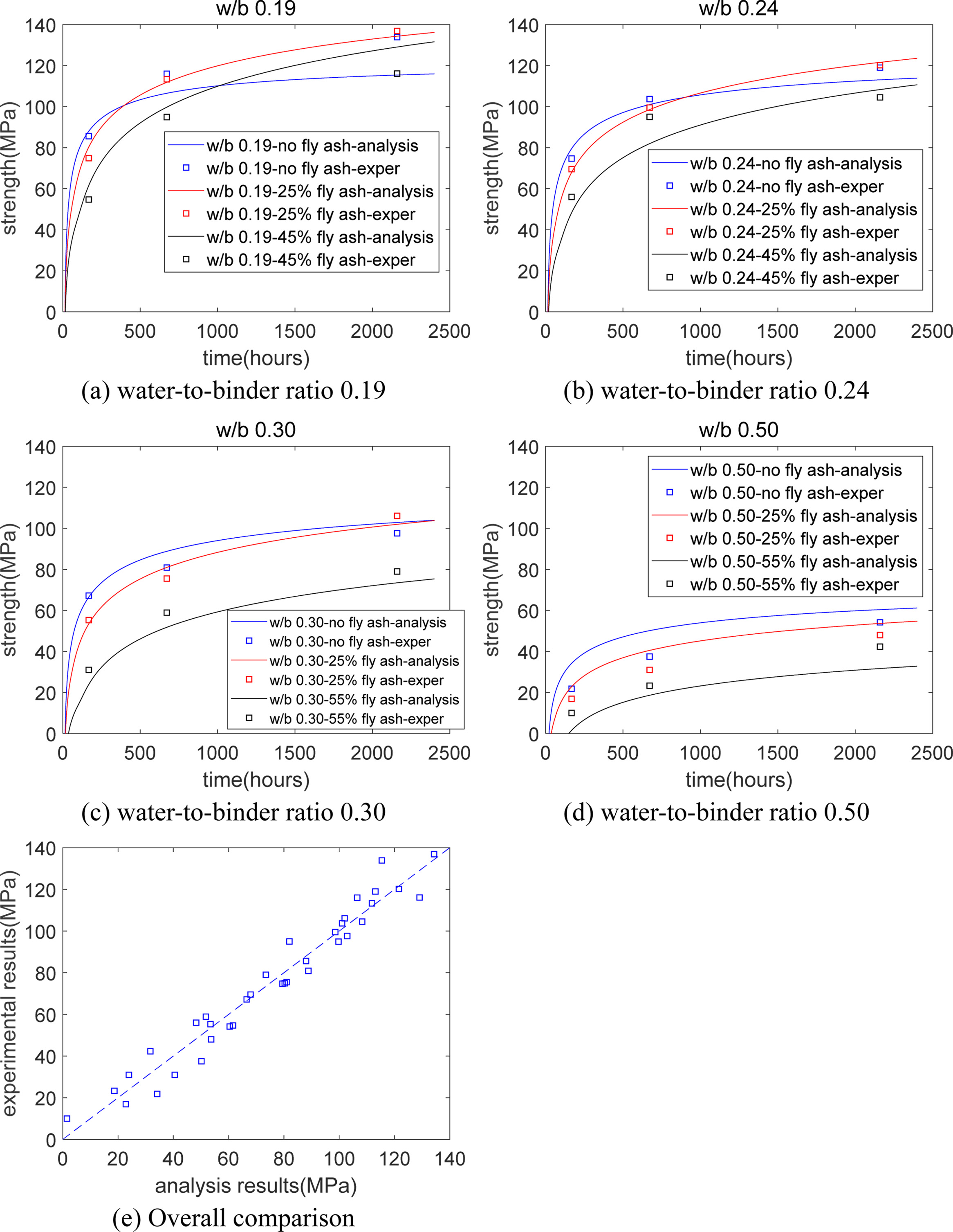
Fig. 6 shows the strength development. First, Fig. 6(a) shows for paste that has a low water-to-binder ratio 0.19, in the early age, the strength of the binary composite paste is gloomier than that of plain paste. Meanwhile, at a late age, because of the evolution of pozzolanic reaction, the strength of the blended paste can exceed the plain paste [27]. As the fly ash-to-binder ratio increases, the time akin to strength crossover retards [1]. This is because the reaction amount of fly ash decreases as the fly ash-to-binder ratio increases (shown in Fig. 4). Second, from Fig. 6(a-d), as the water-to-binder ratio increases, the time akin to strength crossover retards. This is because the dilution effect is a lot more apparent for concrete that has a low water-to-binder ratio [28]. Third, as the fly ash-to-binder ratio and water-to-binder ratio increase, the intercept of the strength curve on the x axis increases. This trend of intercepts is comparable to the trends of the final setting of concrete, which increase when water-to-binder ratio or fly ash-to-binder ratio increases [29, 30]. Fourth, Fig. 6(e) shows that analysis outcomes generally accept experimental outcomes. The correlation coefficients between the analysis results and the experimental answers are 0.95. Summarily, the suggested strength development model is applicable for ordinary-strength (water-to-binder ratio 0.5), high-strength (water-to-binder ratio 0.3), and ultra-high-strength (water-to-binder ratio 0.24 and 0.19) concrete that contains various fly ash contents (0%–55%).

This research presented a framework for evaluating the hydration heat, reaction amount, and strength progress of cement–fly ash binary composite.
First, isothermal calorimetry testing with high tem-        peratures was used to indirectly identify the reaction amount of fly ash. According to the experimental outcomes of cumulative hydration heat at various temperatures, by using the hydration heat model considering the contribution of fly ash and cement, the reaction coefficients of a kinetic reaction model of fly ash were determined.
Second, the reaction amount of binders was calculated using the composite reaction model. We discovered that the hydration amount of cement in composite binder is greater than that in plain cement, the reaction amount of fly ash is significantly improved at elevated temperatures, and also the reaction amount of fly ash decreases as the contents of fly ash increase. The suggested blended hydration model is applicable for various mixtures at both early and late ages.
Third, in line with the reaction amount of fly ash and cement, we proposed a straight-line equation for evaluating the strength progress of binary composite. The results of the analysis can reflect the crossover of the strength progress of fly ash composite concrete. As the content of fly ash and the water-to-binder ratio increase, the threshold time of strength development increases, and the time akin to strength crossover retards. The dilution effect is apparent for concrete that has a low water to binder ratio.
Fourth, the suggested model is applicable for ordinary-strength, high-strength, and ultra-high-strength concrete with assorted fly ash contents and water-to-binder ratios. The coefficients of hydration model, heat model and strength model are constants for a number of mixtures. The suggested hydration heat-strength progress model is helpful for material style of concrete that contains fly ash.

This research was supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF), funded by the Ministry of Science, ICT & Future Planning (No. 2015R1A5A1037    548), and an NRF grant (NRF-2020R1A2C4002093).