A series of Co_1-xZn_xFe₂O₄ ferrites with x = 0.0, 0.1, 0.2, 0.3, 0.4, 0.5 were synthesized using the standard double sintering ceramic technique. The single-phase cubic spinel structure of the samples was confirmed from the X-ray diffraction patterns and the sharp high intensity peak revealed that the samples are in good crystalline form. The lattice parameters were observed to increase with the increasing of Zn concentration. By increasing the concentration of Zn content, a significant increase in the density and a subsequent decrease in porosity and grain size were observed. The dielectric constant (ε′) of the sample is found to decrease with the increase in frequency. Dielectric relaxation peaks were observed for the frequency dependence of dielectric loss curves. The dc resistivity at different temperatures was studied and all the samples were of semiconductor nature. The saturation magnetization was found to be reduced as the Zn substitution was increased and consequently permeability decreases.

Keywords: X-ray diffraction, SEM, Permeability, Dielectric, Anisotropy Constant

The spinel ferrite, MFe₂O₄ (M=Co, Mn, Ni, Zn etc.) with general formula (M_δFe_1−δ)[M_1−δFe_1+δ]O₄ where, δ represents degree of inversion [1, 2] have remarkable electrical and magnetic properties that can be tuned by ion substitution. Such materials are considered as promising candidates for microwave and magneto-optic devices, high-frequency catalysis, magnetic drug delivery, magnetic resonance imaging (MRI), radio-frequency hyperthermia and high-density recording medium [1-3]. Cobalt ferrite (CoFe₂O₄) has a high cubic magneto-crystalline anisotropy, high coercivity and moderate saturation magnetization [3]. These properties of cobalt ferrite can be tuned by substituting various metal ions in the ferrite lattice. Substitution of small amount of non-magnetic Zn ions generates cation redistribution in the octahedral [B] and tetrahedral [A] sites of the spinel structure which makes changes in the saturation magnetization and coercivity of the materials [4]. In CoFe₂O₄ ferrites Co²⁺ ions occupy octahedral [B] sites and Fe³⁺ ions are equally distributed between tetrahedral and octahedral sites. It is reported that Zn²⁺ can continuously migrate to tetrahedral and octahedral positions which has significant impact on the magnetic and electrical properties of ferrites [4]. Therefore, sub-   stitution of Zn²⁺ in CoFe₂O₄ makes it a hard magnetic material with high Curie temperature and good chemical stability [5]. Co-Zn ferrite is suitable in high frequency magnetic applications, magnetic recording applications (audio–video tapes) and high-density digital recording disks etc. [6] because of its high electrical resistivity and negligible eddy current losses. There are many reports on Co-Zn ferrites synthesis in the literature. A. Khan et al. [7] by ceramic method, S. Singhal et al. [8] by sol-gel-route, S. Tapdiya and A.K. Shrivastava [9], M.T. Jamil et al. [10] by chemical co precipitation method, R. Rani et al. [11] by solution combustion method, S.T. Alone and K.M. Jadhav, [12] by wet chemical co-operation technique prepared the samples. In this paper, Co_1-xZn_xFe₂O₄(x=0.0-0.5) ferrites are synthesized by cost effective double sintering solid state reaction method [7] which involves amalgamating the powdered particles together through solid state diffusion process at an elevated temperature below the melting points of the constituents. This is a two-step process where the pre-sintering stimulates phase formation and sintering expedites grain growth with densification. As such, the prepared samples are less porous, denser, harder and has greater flexural strength [7, 13]. Thus, the sintering process gives a microstructure of the samples with conductive grains and improves grain boundaries. But the temperature and duration need to be chosen carefully in order to attain the particular characteristics of the samples. Moreover, sintering process prevents deformation and cracking of samples. Here, we have carried out direct substitution of nonmagnetic Zn²⁺ for Co in cobalt ferrite by double sintering process in order to investigate the effect on magnetic behavior. Zn²⁺ substitution is likely to affect the cation distribution and thereby significantly alter the magnetic properties.

All ferrite samples were synthesized by double sintering ceramic process. The materials used in this study were CoO, Fe₂O₃ and ZnO and mixed together to form the composition of Co_1-xZn_xFe₂O₄(x = 0.0-0.5) where “x” is the Zn concentration in CoFe₂O₄ ceramic compound. Mixtures of these raw materials were grinded into extremely fine powder for 4 hours. The prepared powder was kept in programmable furnace for calcination process. The calcination temperature was 750 ^oC and it was calcined for 3 hours. After calcination, they were grinded again. Finally, the pellets were made from the powders using hydraulic pressure. Then the samples were sintered for 2 hours at 1050 ^oC.
 
Characterization
The crystalline and cubic spinel structure of the ceramic samples was studied by an X-ray Diffracto-   meter (XRD) using PHILLIPS PRO XRD SYSTEM in the 2θ range from 20^o to 70^o. The specimens were exposed to CuK_α radiation of wavelength, λ = 1.54178 Å with a primary beam of 40 kV and 30 mA with a sampling pitch of 0.02^o and time for each step data collection was 1.0 sec. The lattice parameter of the synthesized samples was estimated using the relation [2]
 

 
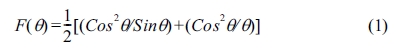
where, q is the Bragg’s angle [14].
The X-ray densities of the samples were estimated using the relation [2]
 

 
where Z is the number of molecules per unit cell of spinel lattice, M is the molecular weight of the samples, N is the Avogadro’s number and a is the lattice parameter of the samples.
The bulk density of the samples was calculated by using the formula
 

 
And we have measured the porosity of the samples using the formula given below,
 

 
The surface morphology and compositional features were studied using a scanning electron microscope (FEI SEM). dielectric and permeability measurements were conducted by Impedance Analyzer (WAYNE KERR PRECISION-6500B). The real part of dielectric constant was calculated using the formula,
 

 
Here, C is the capacitance of the pellet, L is the thickness or height of the pellet, A is the area of cross-section of the flat surface of the pellet,  is the dielectric constant at free space.
The imaginary part of the dielectric constant is,
 

 
with tand being the loss tangent.
The quality factor was measured using the formula
 

 
The initial permeability was measured by using the formula [15]
 

 
Where, L_s is the inductance in Henry, N is the number of turns of copper wire in the torroid, D_outer indicates the outer diameter and D_inner stands for the inner diameter of the torroid.
To determine the temperature dependent resistivity, “KEITHLEY 6514 SYSTEM ELECTROMETER” a small oven and a thermocouple-based thermometer had been used.
The resistivity was calculated using the formula,
 

 
Where, r denotes the specific resistance, L is the length of the specimen and A indicates the area of cross section.
Magnetic properties of the samples were measured by a Vibrating Sample Magnetometer (EV9 MICROSENSE VSM). All the hysteresis magnetic measurements were carried out at room temperature. Anisotropy constant has been calculated by using the formula,
 

 
with H_c is Coercive field and M_s denotes Saturation Magnetization.

Structural Properties
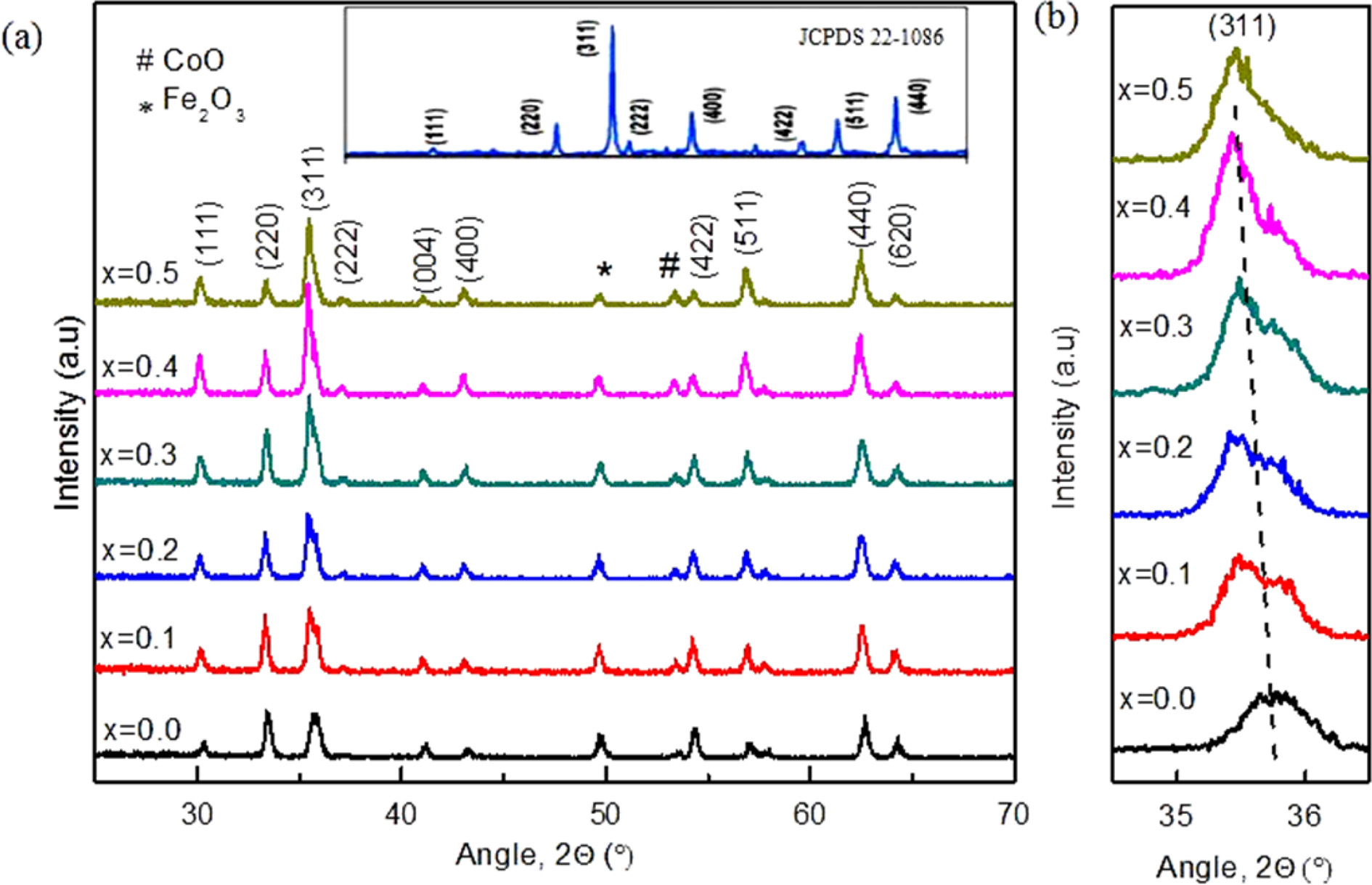
The structural characteristics of Zn doped Cobalt ferrites with compositions of Co_1-xZn_xFe₂O₄(x = 0.0-0.5) were measured by X-ray diffraction technique shown in Fig. 1. The miller indices were indexed according to JCPDS card no 22-1086 [16]. The fundamental reflections from the planes of (220), (311), (511), (440) are charac-   terizing the single-phase cubic spinel structures [17]. The sharp peak reveals that the samples are in good crystalline form. Reflection from the other planes (400), (422) has also been observed with weak intensities. Impurity peaks for Fe₂O₃ and CoO were detected which suggests the occurrence of a few unwanted chemical reactions at the time of sintering. In this sample, it is observed that the highest intensity peak was shifted to lower angle with the increase of Zn content (Fig. 1(b)). This shifting of highest intensity peak towards lower angle is attributed to have higher inter-planar distance and increase in cell volume. The intensity of the highest peak is found to increase with increase of Zn content which indicates the crystalli-   zation and spatial position of the substituted atom. 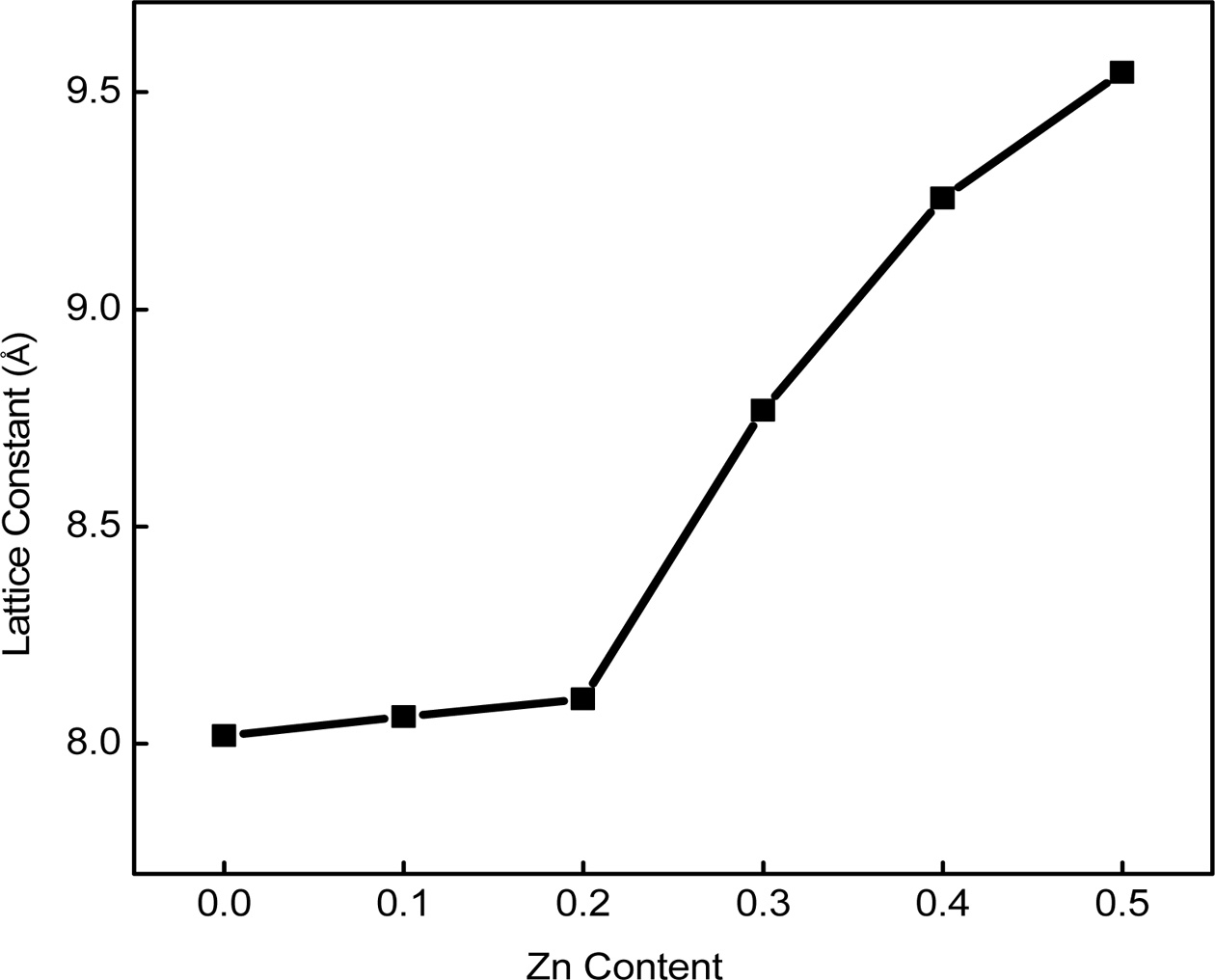To determine the exact value of lattice parameter, Nelson-Riley (N-R) extrapolation method was used [2]. The effect of Zinc substitution on the lattice constant is shown in Fig. 2. From this figure, it is found that the lattice parameter enhances with the increasing Zn content. This increment may be related to the replace-   ment of Co²⁺ ion with smaller ionic radius (0.745 Å) [18] by Zn²⁺ ion with larger ionic radius (0.82 Å) [19]. During the crystallization process, the unit cell expands to assemble the substituted large Zn²⁺ ions. Thus, the addition of Zn²⁺ in the Cobalt ferrite is expected to increase the lattice parameter. Similar trend has been reported in Zn-Mg-Cu [20]; Zn-Mg [21] and Ni-Zn [22] and Cu-Zn [2] ferrites. 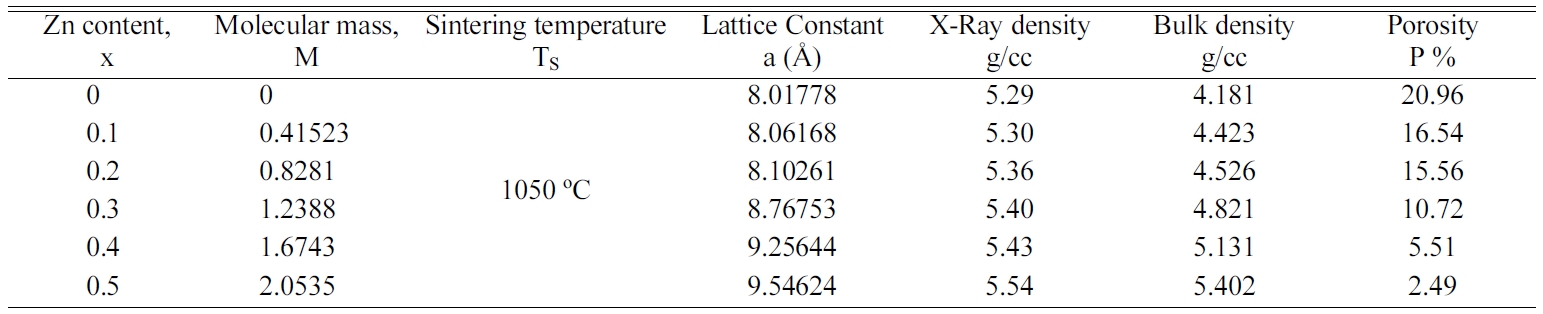The effect of Zn substitution on lattice parameter, X-ray density, Bulk density and porosity is shown in Table 1.
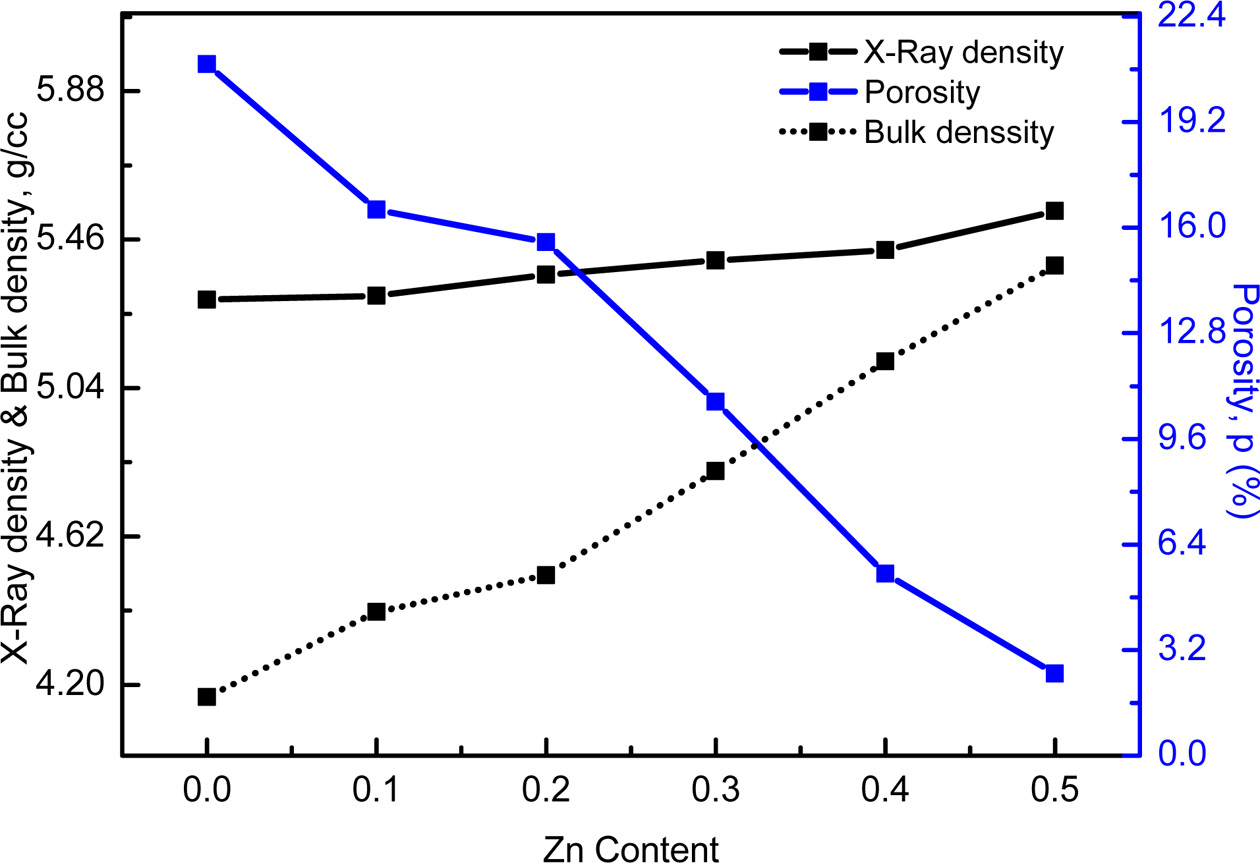
It is observed from Fig. 3 that the X-ray density, ρ_x and bulk density, ρ_B increase increase with increasing Zn content. The increase in X-ray and bulk density may be due to the increase in molecular weight of the various compositions of Co-Zn ferrites. Generally, the homo-   geneous distribution of any element in other element may increase the density. This significant increase of the density can be explained by the introduction of Zn ions through sintering and lattice diffusion. The lattice diffusion increases the diffusion path length which in turn accelerates the rate of cation inter-diffusion in the samples [23]. As a result, the density increases with the introduction of Zn content. It is also observed from this figure that the X-ray density is higher than the bulk density. This might be evolved with the existence of pores on the macroscopic scale and vacancies in the lattice on atomic scale during the sintering process or at the time of sample preparation [13]. The smaller value of bulk density, ρ_B compared to the X-ray density, ρ_x might be due to the presence of inter-granular porosity. On the other hand, porosity exhibits completely opposite trend as shown in Fig. 3. The porosity is found to decrease with the increase in Zinc content as the samples become denser. Similar results were observed in several ferrites [3, 13, 24, 25].
The microstructures of the investigated materials are given in Fig. 4. The grain size remained almost same for the lower Zinc substitution (x = 0 to 0.3) but for higher Zn content (x = 0.4, 0.5), the grain size was found to decrease as ZnO hinders the grain growth during sintering to stabilize the crystallization. The grain growth amplifies the migration of the pores to the grain boundary and hence, increases the sintered density. Grain boundaries expand over the pores during the sintering which might produce the denser material by reducing the pores volume [25]. The pores located at the grain boundaries impede the domain wall move-   ment and impact on permeability and resistivity [26]. It has been reported that Zn²⁺, Cd²⁺, Zn²⁺, Ti⁴⁺, Nd²⁺ substitution do not favor the grain growth [27-29].
 
Dielectric Properties
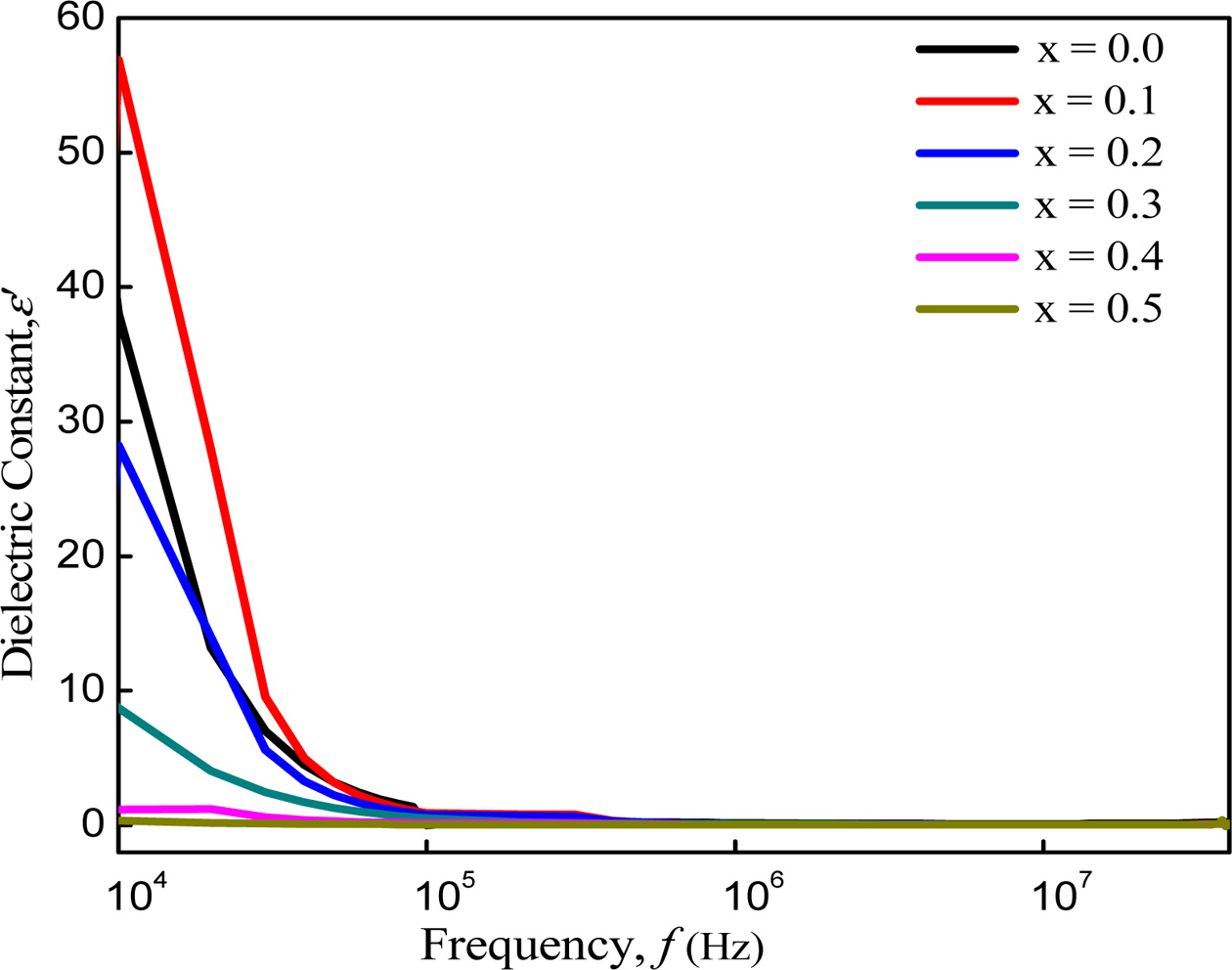
The variation of the real part (e ') of dielectric constant with frequency from 10 kHz to 40 MHz at room temperature are shown in Fig. 5. The dielectric constant (e ') decreases with increasing frequency, which is rapid at lower frequencies and slower at higher frequencies. At much higher frequency it is very small and becomes independent of frequency. Similar dielectric behavior is observed in Mg-Cu-Zn ferrites [30], Ni-Cu-Zn ferrites [31] and Cu-Zn ferrites [32]. All the samples have high value of dielectric constant in the order of 10³-10⁵ at low frequencies. Maxwell-Wagner interfacial type of polarization can describe these higher values at lower frequency region [33, 34, 13] for the inhomogeneous double layer dielectric structure. This is normal dielectric behavior observed in most of the ferromagnetic materials in room tem-   perature. Sintering temperature and time or atmosphere including grain structure can influence the Fe²⁺ ions concentration which is a characteristic property of a ferrite material. Fe²⁺ ions availability allows the electron to exchange between the +2 and +3 valance states of Fe ions and creates the local displacement of charges in the direction of the applied electric field. This in turn causes the dielectric polarization of the ferrites. The electron exchange was assumed to increase with the increased concentration of Fe²⁺/Fe³⁺ ions pairs on B-site. However, as the frequency of the alternating field is increased, the electron exchange between Fe²⁺ and Fe³⁺ ions cannot follow the alternating field beyond a certain frequency and then the dielectric constant becomes constant [28, 32].
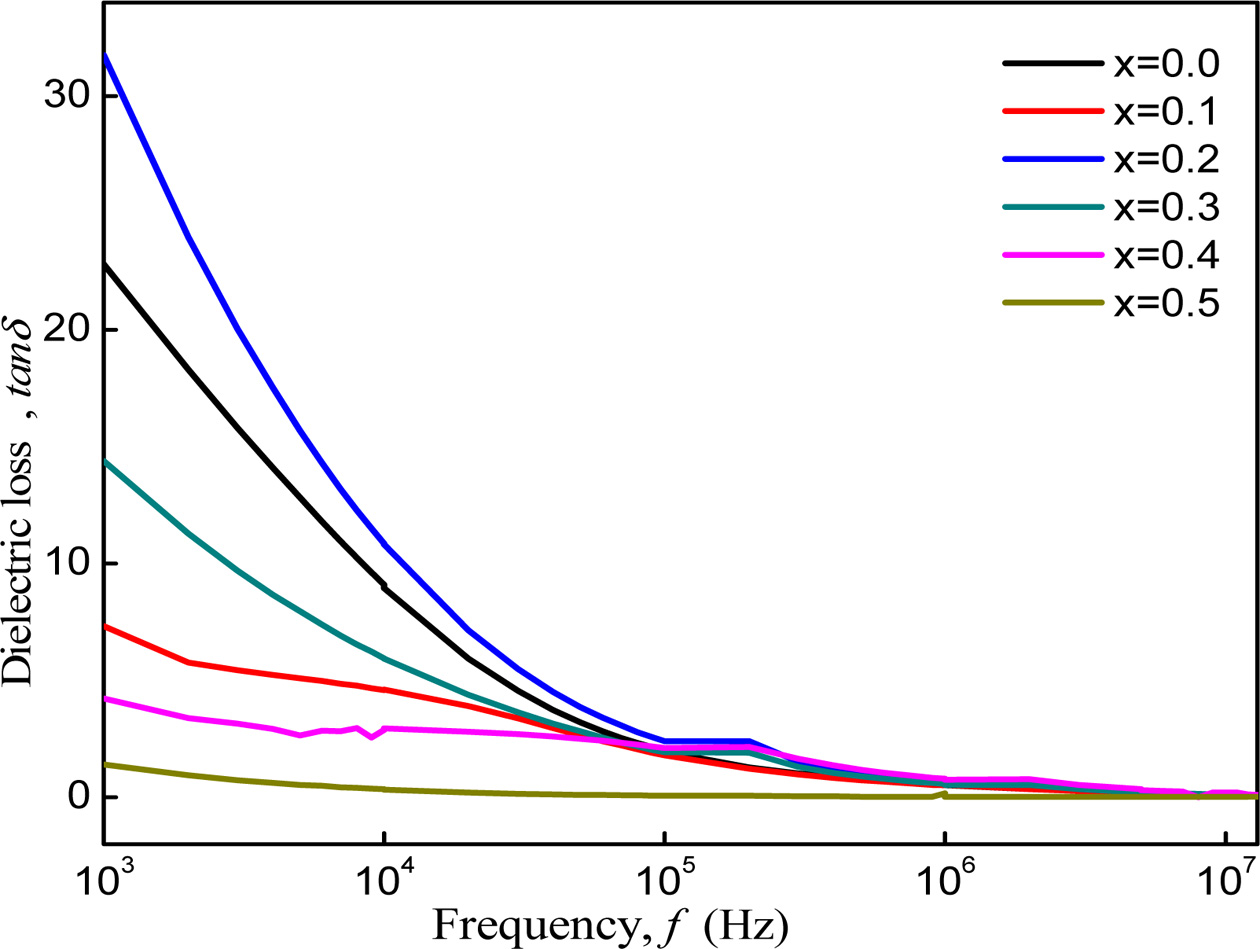
Fig. 6 shows that dielectric loss decreases rapidly with increasing frequency and becomes constant at higher frequency range. In the high frequency the conduction in between Fe²⁺ and Fe³⁺ ions increases which corresponds to low resistivity and small energy is required for electron exchange at the octahedral site results in lower value of dielectric loss [32].
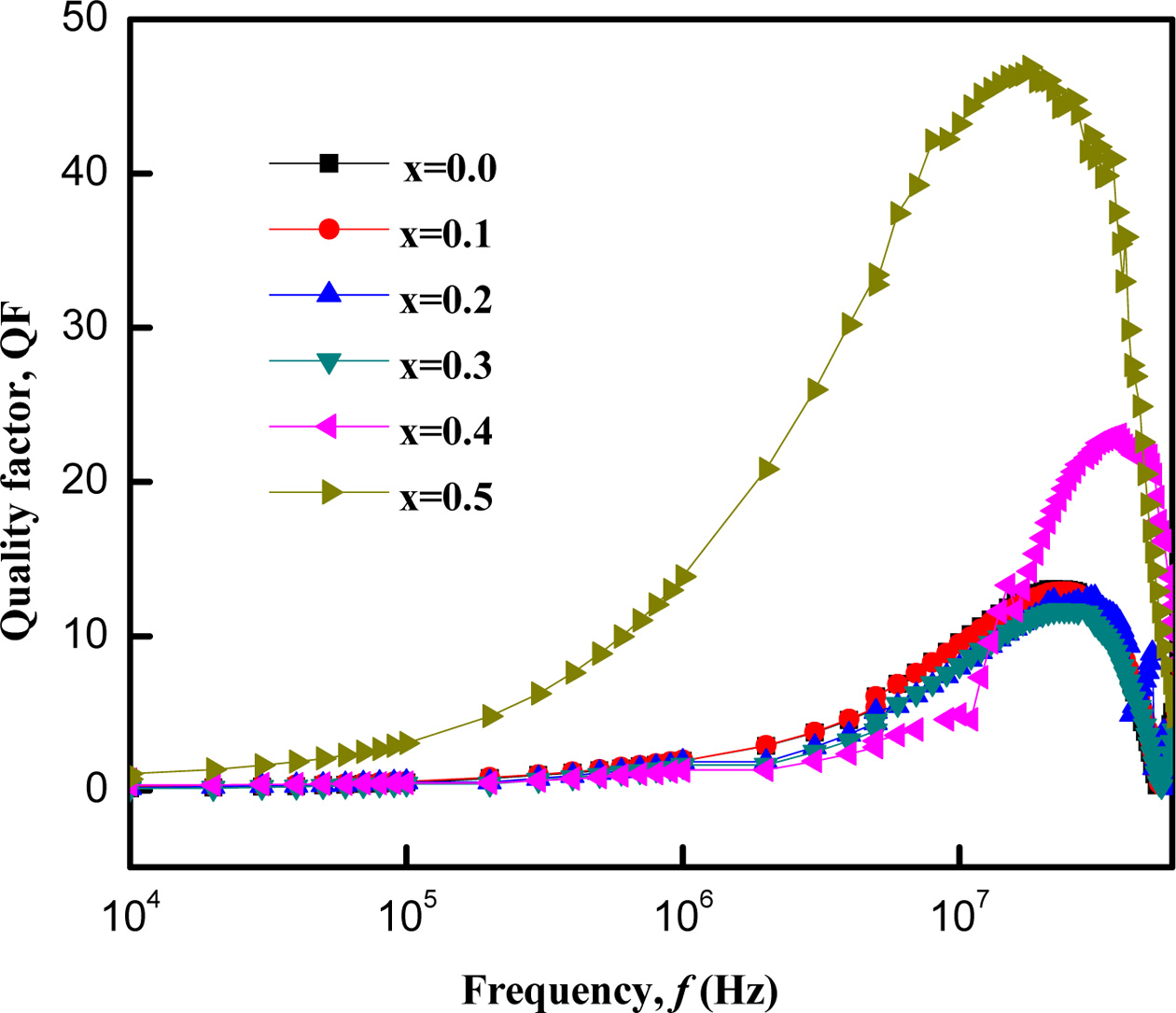
Fig. 7 shows the variation of Q factor with frequency as log f for the samples. All the samples show a maximum at a certain frequency. The appearance of a maximum can be described by the relaxation formula, wt = 1, where, w = 2pf_max and relaxation time, t = 1/2p, p is the hopping probability per unit time [35]. As stated by this relaxation relation, a maximum can be appeared when the hopping frequency of electron between Fe²⁺ and Fe³⁺ ions at the adjacent B-sites and the frequency of applied AC field exactly match with each other [28, 32]. It is also observed that f_max or the hopping probability per unit time increases for the samples with Zn content. Therefore, the concentration of the Fe²⁺ ions on the B-sites increases in these samples which is also consistent with the resistivity data.
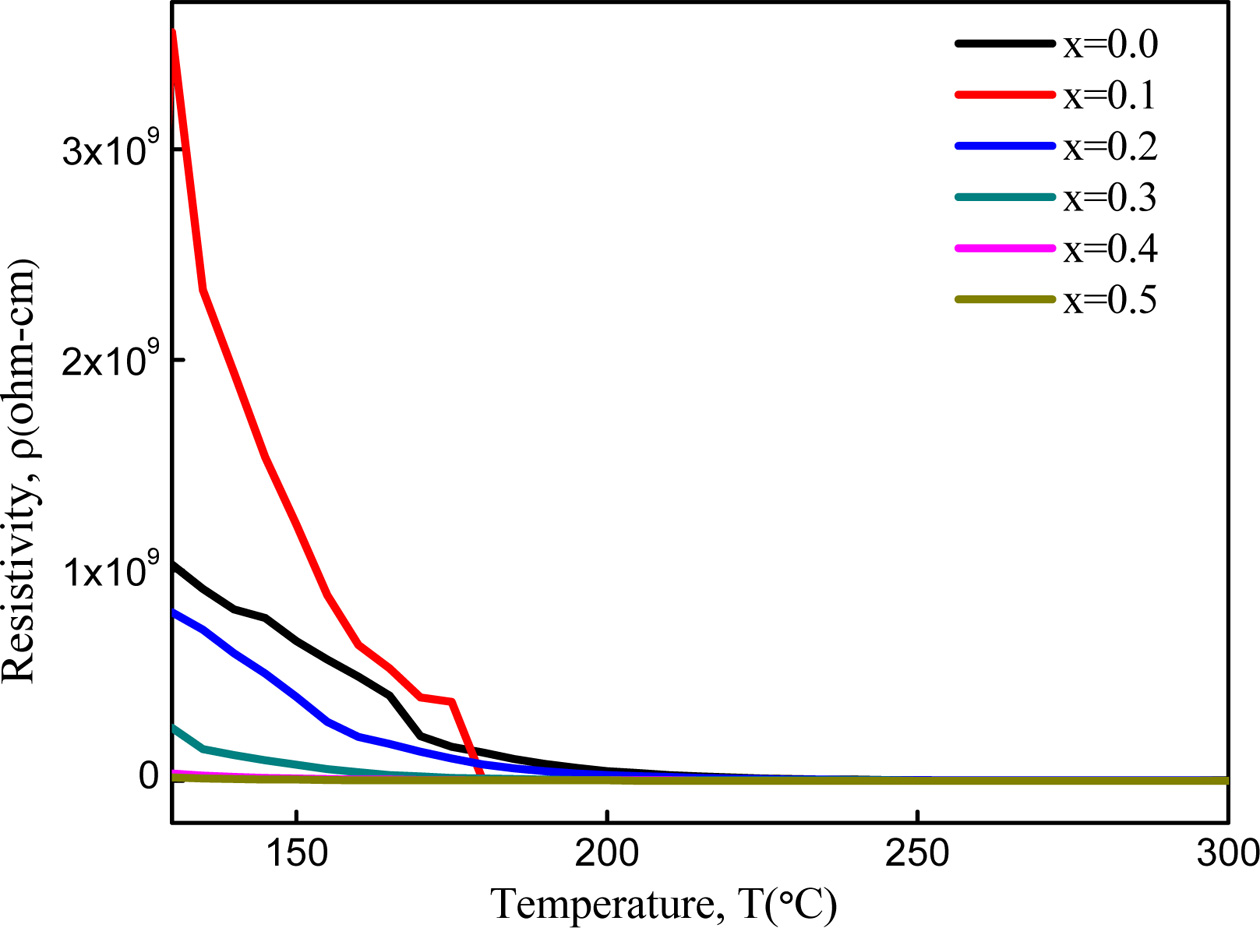
Fig. 8 shows that the DC resistivity decreases with the increase in temperature for the samples which is the normal ferromagnetic behavior. Generally, the hopping of electrons between Fe²⁺ and Fe³⁺ ions at adjacent B-sites starts to get thermally activated with the increase in temperature and produce local displacement in the direction of the applied AC field. In the low tem-   perature region, the resistivity, r starts to decrease gradually because the thermal energy breaks the localized dipoles and starts orienting themselves in the low temperature region. The orientation of these dipoles becomes more significant with the increase of temperature, as the exchange of charge carriers between the Fe³⁺ and Fe²⁺ ions on octahedral sites [34, 36] increases and this exchange decreases the resistivity of the samples. The intensified chaotic thermal oscillations at high temperature are responsible for this negligible small resistivity [36].
It is observed that for x = 0.1, the dielectric constant as well as the value of resistivity are greater than the pure Cobalt ferrite. This sample may have higher dielectric properties and low eddy current loss than the other samples.
 
Magnetic Properties
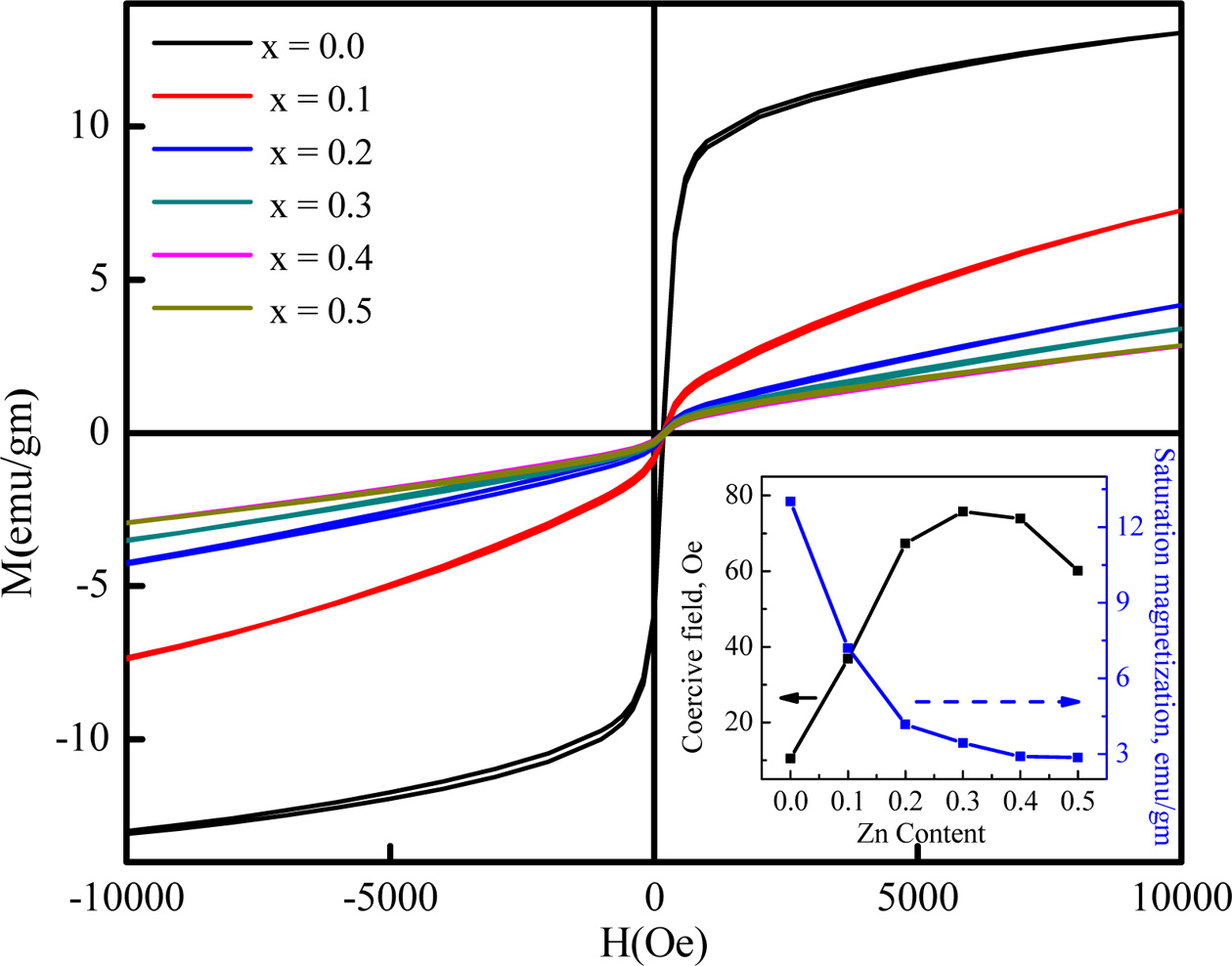
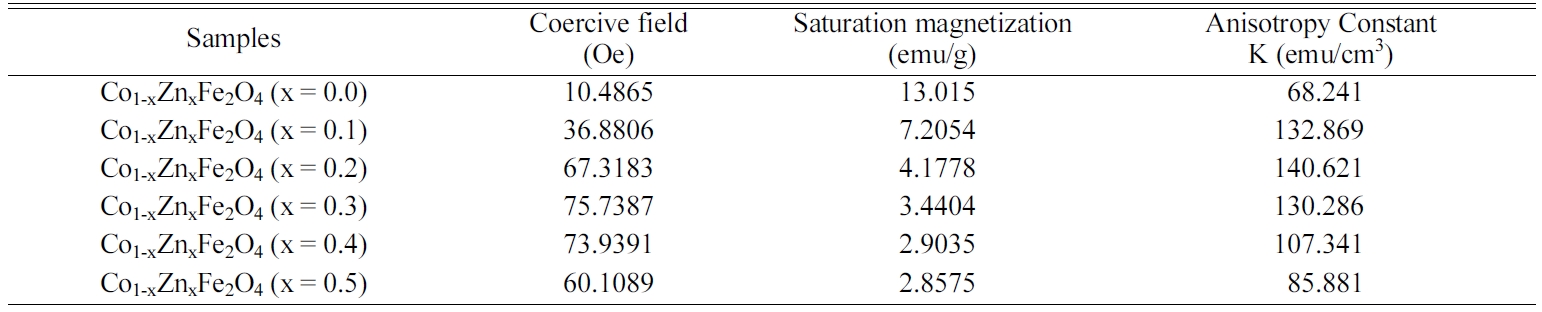
Figure 9 shows that the saturation magnetization decreases with Zn content. Table 2 shows the variation of coercive field, saturation magnetization and anisotropy constant with increasing Zn content in Cobalt ferrites. According to Néel's sublattice model, resulting magneti-   zation depends on the difference between B and A-site magnetization, provided that the sites are collinear and antiparallel to each other. In Co-Zn ferrite, Fe³⁺, Fe²⁺, Co²⁺ and Zn²⁺ elements have magnetic moment of 5 µB, 4 µB, 3 µB and 0 µB respectively which is coming from ‘d’ orbital electron distribution [25]. All the elements can migrate to both A- and B-sites. The possible cation distribution of CoFe₂O₄ can be presented as:
 

 
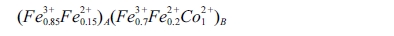
In case of CoFe₂O₄, most of the Fe³⁺ and a smaller part of Fe²⁺ take place on the A sites, and remaining Fe³⁺, Fe²⁺, Co²⁺ goes to the B sites. For Co_1-xZn_xFe₂O₄, the non-magnetic ion Zn²⁺ takes places to the octahedral site along with the magnetic ion, Co²⁺. Basically, the Zn²⁺ and Co²⁺ replace the Fe²⁺ and Fe³⁺ in octahedral sites, forcing a migration of Fe²⁺ and Fe³⁺ to the tetrahedral sites [4]. The presence of large magnetic moments (caused by the Fe³⁺ and Fe²⁺ ions) on the A-sites increases the A-site magnetization which in turn leads to a decrease of overall magnetization. The saturation magneti-   zation was found to decrease significantly from 13.015 emu/g to 2.85 emu/g with Zn substitution.
Here, from the inset of Fig. 9, the coercivity is noticed to increase with the enhanced concentration of zinc ions while the saturation magnetization behaves completely opposite which can be described by Browns relations [25]. The high coercive force confirms that the cobalt ferrite becomes hard from soft ferrite after Zn substitution. Anisotropy constant represents the energy required to deflect the domains from the “easy” to “hard” positions. The interaction between spin magnetic moment of each atom and crystal lattice determine the easy and hard alignments of the compounds. The change in anisotropy constant is similar to the change in coercive field. It is observed from the change of anisotropy constant with increasing Zn contents that cobalt ferrite behaved as “soft” magnet at the lower concentration of Zn (x = 0.1,0.2). At x = 0.3-0.5, the ferrite showed the characteristics of “hard” magnet.
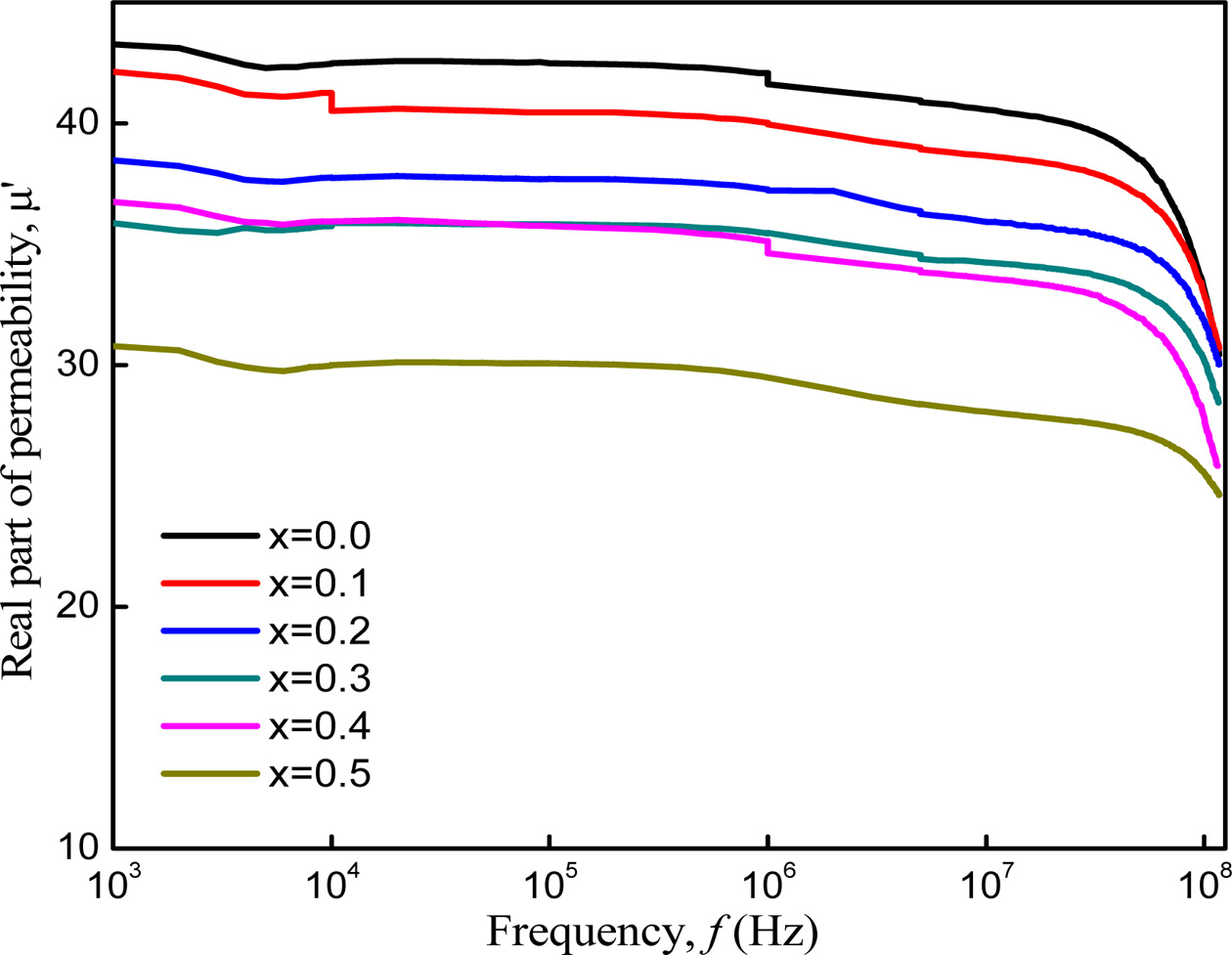
The complex permeability measurements on toroid shape specimens have been carried out at room temperature for all the samples of series Co_1-xZn_xFe₂O₄ (x = 0.0-0.5) in the frequency range 1 kHz-100 MHz. The variation of μ' with frequency is shown in Fig. 10. It is found that the value of initial permeability (μ') shows flat profile up to a certain frequency (> 10⁷ Hz) indicating good low frequency stability and then it falls rapidly to a very small value after a certain high frequency named as Cut-off frequency. The permeability of polycrystalline ferrite is related to spin rotation and domain wall motion. And Globus- Duplex model [28] says that the permeability caused by wall motion is linearly dependent on the grain size. From the micro-   structure analysis of this work, it is noticed that the grain sizes decrease with increasing Zinc concentration and domain wall movement is influenced by grain size. Also, the decrease of permeability is associated with the decrease in domain wall movement. On the other hand, the saturation magnetization was found to be decreased in our case, which decreases the number of domain walls within the grain according to Globus relation [13, 37]. Therefore, the permeability is expected to decrease with the addition of Zn content. At high frequencies, the nonmagnetic impurities between intra-granular pores influence both spin rotation and domain wall motion so that permeability decreases at higher frequencies.
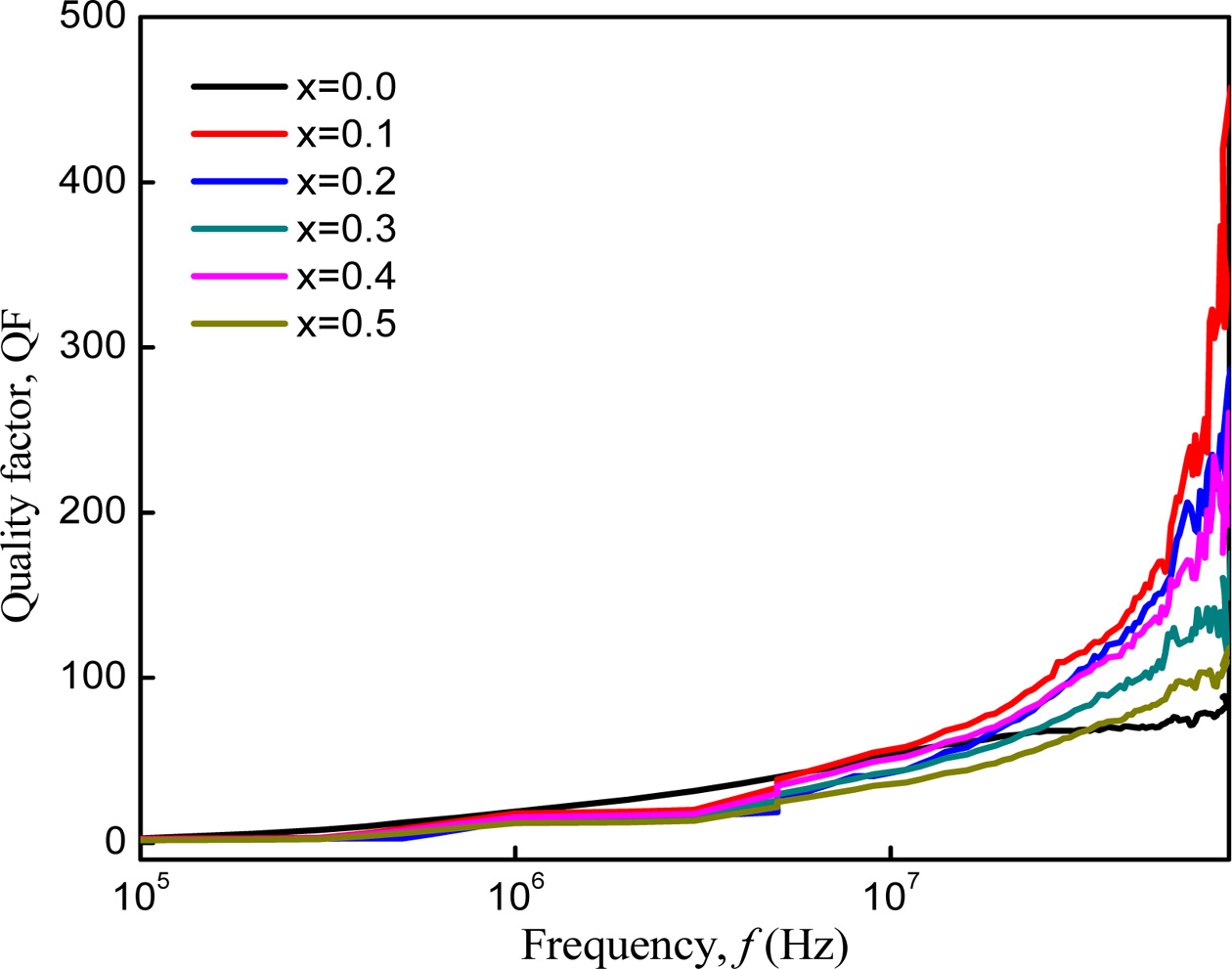
Fig. 11 shows the variation of Quality factor (QF) with frequency of Co_1-xZn_xFe₂O₄ (x = 0.0-0.5) that determines the efficiency of the magnetic materials. It increases with increasing frequencies. The Q factor of Co-Zn ferrite samples increased for a small amount of Zn²⁺ substitution and then decreased with addition of Zn. Zn substituted sample has a higher value of QF than the unsubstituted sample. This change of QF depends on magnetic loss and porosity of the samples [28]. Among the samples, Co-Zn ferrite with x = 0.1 has the highest QF which indicates that this sample has the lowest magnetic loss.
From the above discussion, it is claimed that the polycrystalline Co-Zn ferrite is versatile ferrite, due to their high resistivity and low eddy current losses. The adjustable grain sizes and controllable magnetic properties make the applicability of cobalt-zinc ferrite even more versatile. Cobalt-zinc ferrites are suitable for magnetic recording applications such as audio and videotape and high-density digital recording disks etc.

X-ray diffraction measurement confirmed the single-phase cubic spinel structure of polycrystalline samples Co_1-xZn_xFe₂O₄ where x = 0.0-0.5, since no ambiguous reflections other than the spinel structures were evidenced. The lattice parameter was observed to be increased with Zn content substitution. From micro-   structural study, it was observed that the grain size remained almost the same with increasing Zn content. However, the grain size decreased slightly for higher content of Zn. The dielectric constant was found to decrease with increasing frequency, which was rapid at lower frequencies and slower at higher frequencies. DC electrical resistivity increased for 10% of Zn substitu-   tion then again decreased with Zn Content. The saturation magnetization has been decreased and coercive field was increasing for up to 30% Zn content and then started to decrease with increasing Zn content. Permea-   bility decreased with Zn content. From the Dielectric properties and Resistivity measurement, it was observed that 10% of Zn substitution in place of Cobalt increased the dielectric properties and resistivity of the samples. Anisotropy constant is enhanced for x = 0.1, 0.2 and then decreased with higher Zn content.

The authors acknowledge gratefully to Materials Science Division, Atomic Energy Centre, Dhaka and Centre for Advanced Research of Sciences, University of Dhaka, Dhaka, Bangladesh. Authors are sincerely thankful to Nano and Advanced Materials Laboratory, Department of Physics, University of Dhaka. The authors thank the Bose Centre for Advanced Study and Research in Natural Sciences, University of Dhaka for partial support of this work.