Mn_xZn_1-xFe₂O₄ (x = 0.5, 0.6, 0.7) ferrite nanoparticles were synthesized by a thermal decomposition method. The synthesized particles were identified as pure spinel ferrite structures by x-ray diffraction analysis and they were calculated to be 15-20 nm in diameter by the Scherrer equation, depending on the composition. Ferrite nanoparticles are spherical in shape with a slight agglomeration in the FE-SEM image, and the particle size is about 20 nm, which was consistent with the value obtained by the Scherrer equation. The lattice parameters of ferrite nanoparticles monotonously decreased from 8.358 Å to 8.389 Å as the manganese concentration increased from 0.5 to 0.7. As the manganese content increases from x = 0.5 to 0.7, the saturation magnetization value increases from 76 emu/g to 63 emu/g. Mn_xZn_1-xFe₂O₄ toroidal samples were prepared by sintering ferrite nanoparticles at 1,250 ^oC and exhibited faceted grain morphology in FE-SEM images with a grain size of about 3 um regardless of manganese content. The cutoff frequency of the ferrite toroidal sample was estimated to be about 3MHz from the broad maximum point in the plot of imaginary magnetic permeability (μ”) vs. frequencies, which seems to be associated with domain wall resonance.

Keywords: Nanoparticles, MnZn ferrite, Superparamagnetic

MnZn ferrites have attracted much attention due to their high permeability and high electrical resistivity [1-4] and have been used as core materials for choke coils, magnetic amplifiers, power transformers, solar inverters, new energy vehicles DC/DC converters, wireless batteries Chargers, motor stators and many other electronic, automotive and communications equipment today [5-10].
Apart from these applications, MnZn ferrite nanoparticles are also attractive to biomedical medicine as a result of suitable Curie temperature, magnetic crystal anisotropy, moderate saturation magnetization and superparamagnetic behavior at room temperature [11]. They can be used for magnetic resonance imaging (MRI), hyperthermia, modification, detection, isolation and study of cells [12], for isolation of biologically active compounds [13]. If the size of the magnetic particles is smaller than the critical size for the formation of multiple domains, the particles exist in a single domain state and avoid domain wall resonance, which is called superparamagnetic state.
The magnetic properties of nanoparticles can be influenced by the method of synthesis, particle size, cation distribution and composition. Ferrite particles [14, 15] produced by the solid phase reaction between constituent oxides or carbonates have many problems, such as large and non-uniform particle size and induced impurities, which limits the improvement of the products [16, 17]. To overcome these difficulties and meet the requirements for new applications, some wet chemical processes such as coprecipitation [18], hydrothermal techniques [28], sol-gel automatic combustion [29], and thermal decomposition of salts [30-34], citrate precursors [32], and self-propagating high temperature synthesis (SHS) [33] have been considered for the production of ferrite nanoparticles with excellent magnetic properties.
In this study, Mn_xZn_1-xFe₂O₄ (x = 0.5, 0.6, 0.7) nano-    particles were synthesized by a thermal decomposition method in order to obtain ultra-fine nanoparticles with uniform particle size. Their magnetic properties such as the saturation magnetization and magnetic permeability were investigated with VSM (Vibrating Sample Magneto-   meter) and impedance analyzer along with their particle morphologies. In particular, the dependence of the saturation magnetization on the Mn content was described with the number of the paired electron and the unpaired electron.

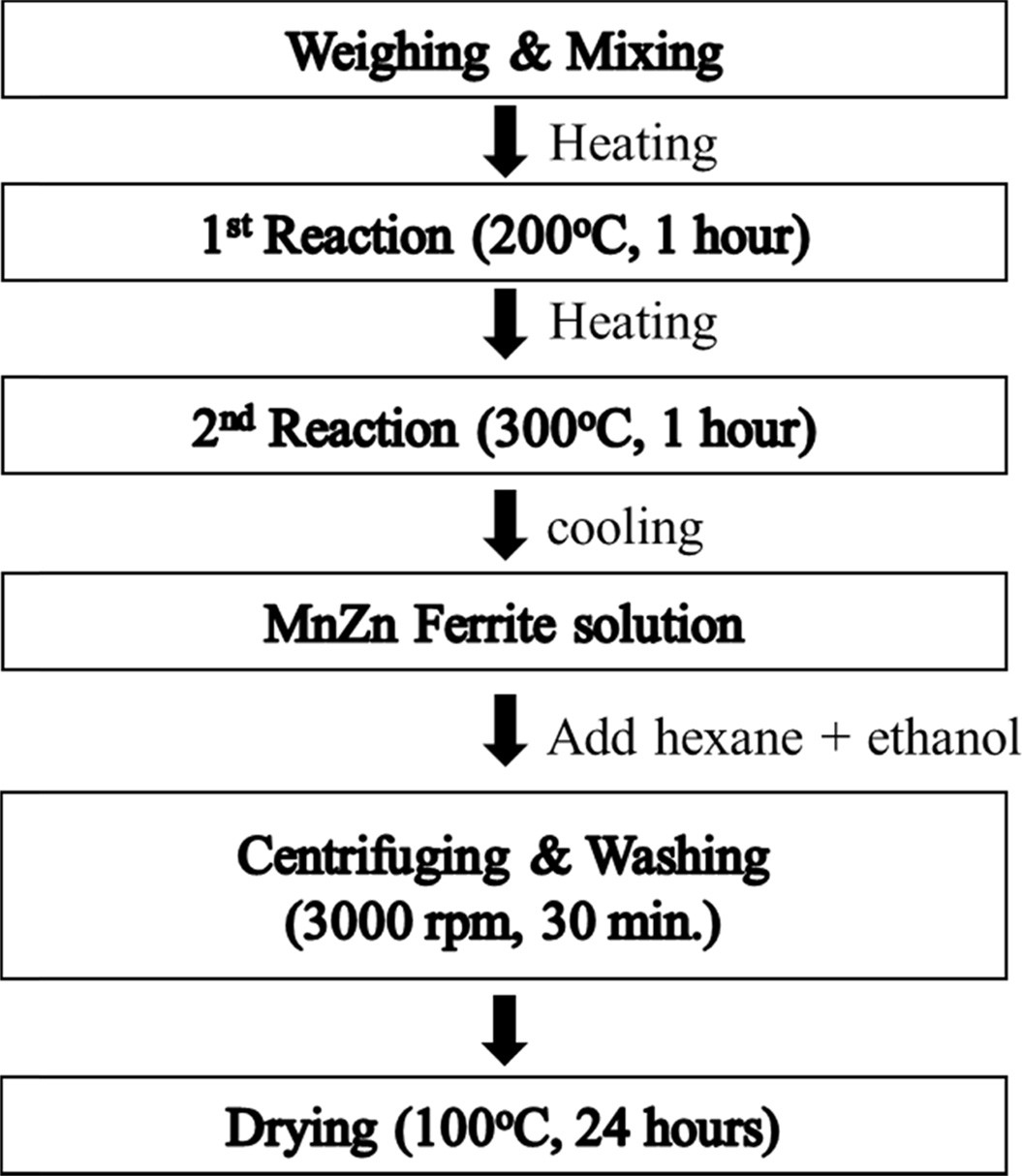
Mn_xZn_1-xFe₂O₄ (x = 0.5, 0.6, 0.7) nano-particles were synthesized by a thermal decomposition method as shown in Fig. 1. Raw materials are Manganese(II) acetylacetonate (97%), Zinc acetylacetonate hydrate (95%), Iron(III) acetylacetonate (97%). Oleic acid (90%) and Oleylamine (70%) were used as a surfactant, 1, 2-Hexadecandediol (90%) as a reducing agent, and Benzyl ether (98%) as a solvent. Mn, Zn and Fe-acetylacetonate precursors were weighed, respectively according to the chemical form of Mn_xZn_1-xFe₂O₄ (x = 0.5, 0.6, 0.7) and poured into a 500 ml three neck flask that was filled with a mixed solution of 6mmol oleic acid, 6 mmol oleylamine, 1,2-hexadecandediol (HDD), and 20 ml benzyl ether. The precursor solution was heated to 200 ^oC for 1 h, then further heated to 300 ^oC and kept there for 1 h, whose process was carried out in N₂ atmosphere with refluxing using cooling water. The solution that finished the reaction was cooled down to room temperature, centrifuged for 30 min at a speed of 4000 rpm and washed repeatedly with hexane and ethanol in order to separate organic remains from the ferrite particles. Hexane was used to dissolve fat acid such as oleic acid and oleylamine. Finally, Mn_xZn_1-xFe₂O₄ (x = 0.5, 0.6, 0.7) nanoparticles was collected and dried at 100 ^oC for 24 h.
Toroidal samples of MnZn ferrites were fabricated by the uniaxial pressing. The ferrite powder was mixed with a PVA (Polyvinyl alcohol, 5 wt.%) binder solution, which was poured into a toroidal shaped mold and applied with a pressure of 1 ton/cm² to make green toroidal samples. The green toroidal samples were burn-out at 650 ^oC for 30 min in air and then sintered at 1,250 ^oC for 2 h under the nitrogen gas ambience.
Phase purity of MnZn ferrites nanoparticles was investigated with X-ray diffractometer (XRD: D/max 2200 V/PC, Rigaku Co., Japan). Microstructures of sintered toroidal ferrite samples were observed with Scanning Electron Microscope (SEM, JSM 6700F, Jeol, Japan). Magnetic permeability (m', m¡È) was measured from 1MHz to 1GHz with Impedance analyzer (E4991A). Saturation magnetization of ferrite particles was measured with VSM (Vibrating Sample Magnetometer).

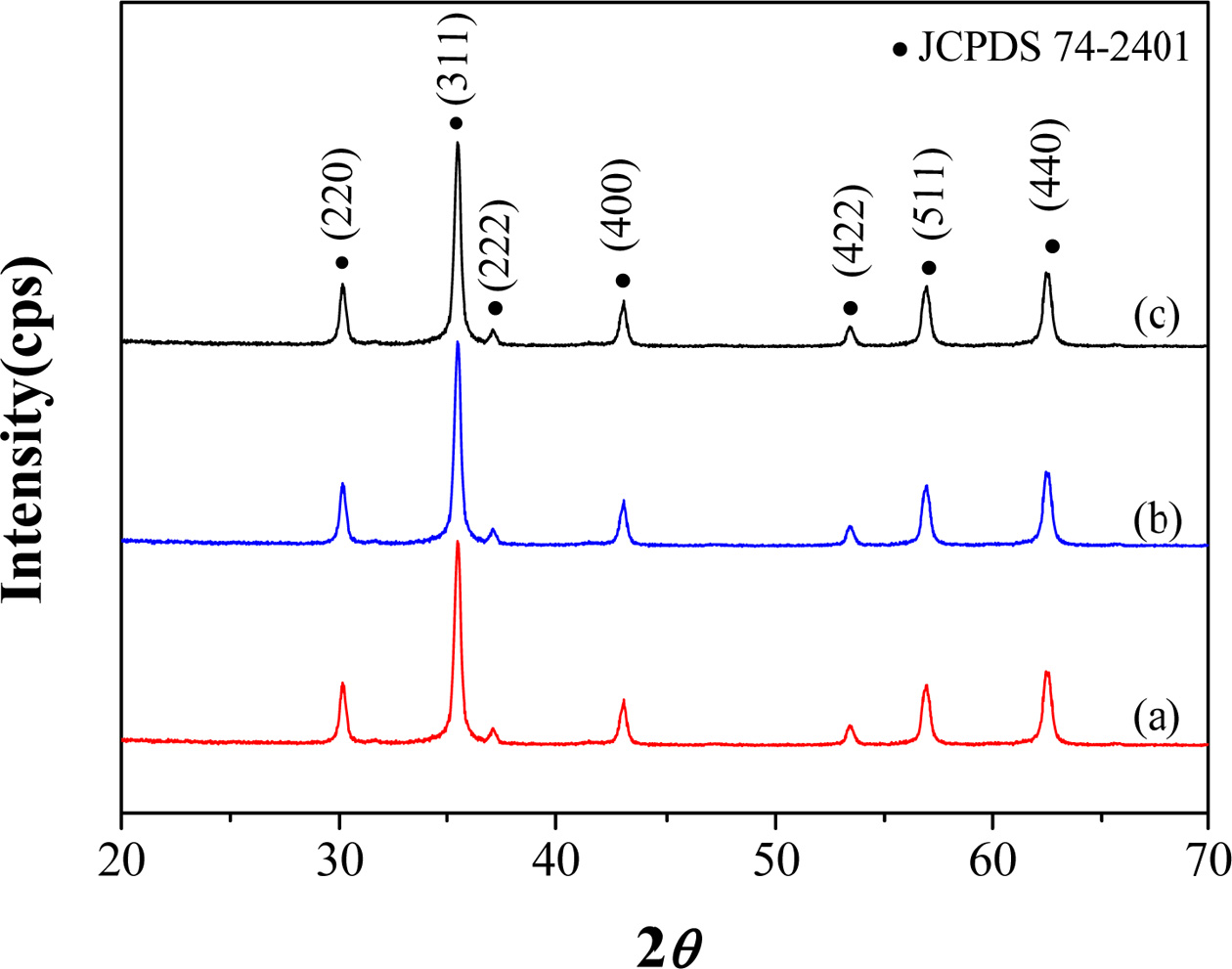
Fig. 2(a)-(c) shows X-ray diffraction patterns of Mn_xZn_1-xFe₂O₄ (x = 0.5, 0.6, 0.7) nanoparticles, which represents a pure spinel structure (JCPDS 74-2401) for all three ferrites without any second phases regardless of composition.
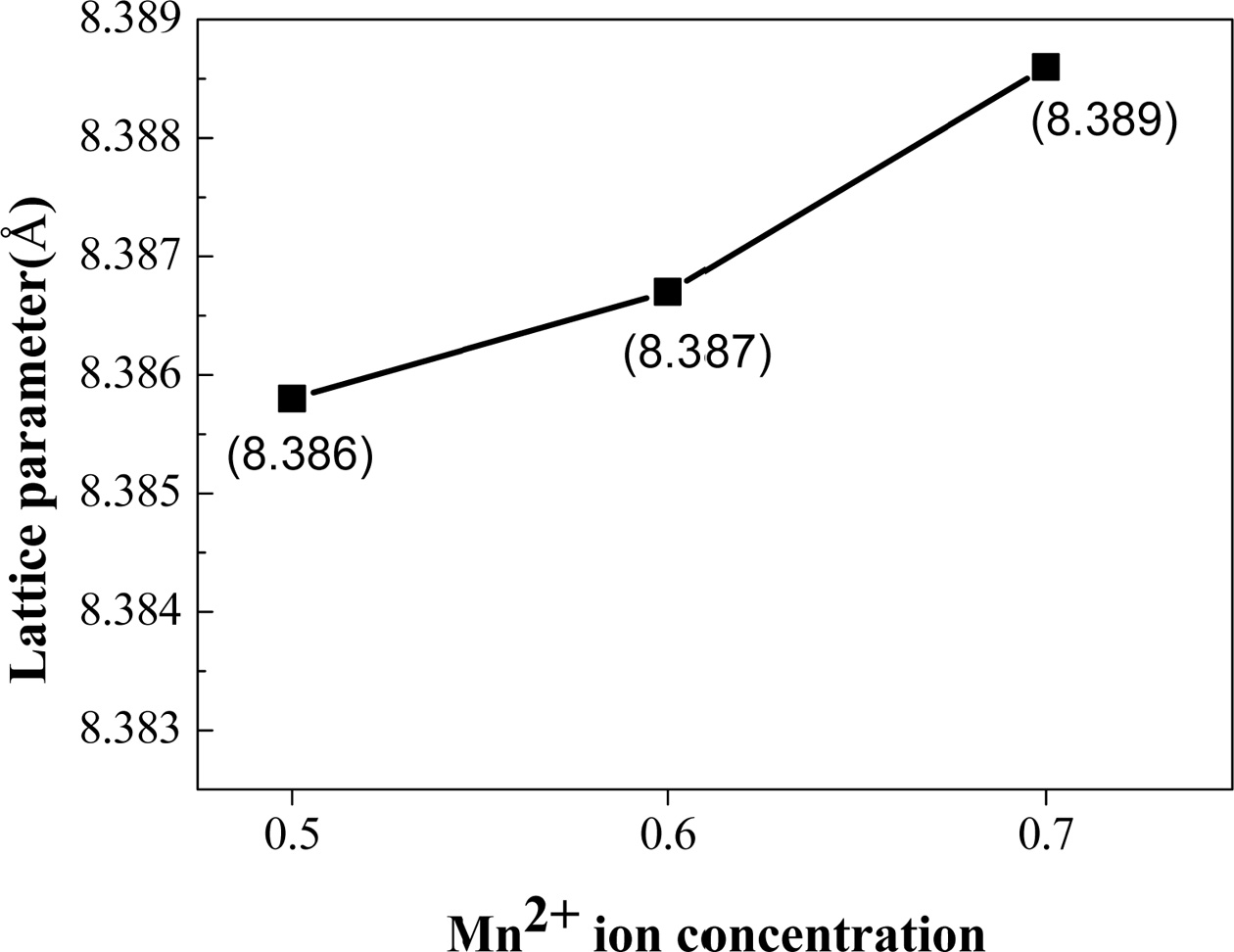
Fig. 3 shows the dependence of the lattice parameters of the ferrite nanoparticles on the Mn concentration, which was calculated by the following equation.
 

 
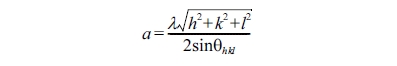
The lattice parameters of Mn_xZn_1-xFe₂O₄ nanoparticles increase continuously and slightly from 8.386 Å to 8.389 Å as Zn concentration increases from x = 0.5 to 0.7 as shown in Fig. 3, which is reasonable considering that the ionic radius of Mn⁺² (0.83 Å) is larger than that of Zn⁺² (0.74 Å). In addition, the incorporated Mn⁺² ions can be thought to occupy the Zn sites well according to not only Vegard¡¯s law [19] but also the fact that both Mn and Zn ions occupy A-sites because MnZn ferrite has normal spinel structure [20].
Spinel ferrite has a chemical form of (A)[B₂]O₄, which is described as a cubic closed-pack of oxygen ions [21-23]. The round and the square brackets represent the tetrahedral interstitial A site and the larger octahedral interstitial B site, respectively. Zinc ferrite is called a normal spinel structure of the form (Zn)[Fe₂] O₄, where Zn²⁺ ions occupy the tetrahedral sites and Fe³⁺ ions occupy the octahedral sites [24]. It was also reported that Mn-ferrite, (Mn)[Fe₂] O₄, the normal spinel structure likewise Zn-ferrite [25].
Fig. 4(a-c) shows the microstructures of Mn_xZn_1-xFe₂O₄ (x = 0.5, 0.6, 0.7) nanoparticles synthesized by the thermal decomposition. Most particles, regardless of Mn concentration, are round shaped and almost identical in size with a diameter of about 20 to 30 nm, which is in good agreement with the crystal size of 24.6 nm, calculated by Scherer's equation [31] using a (311) diffraction peak.
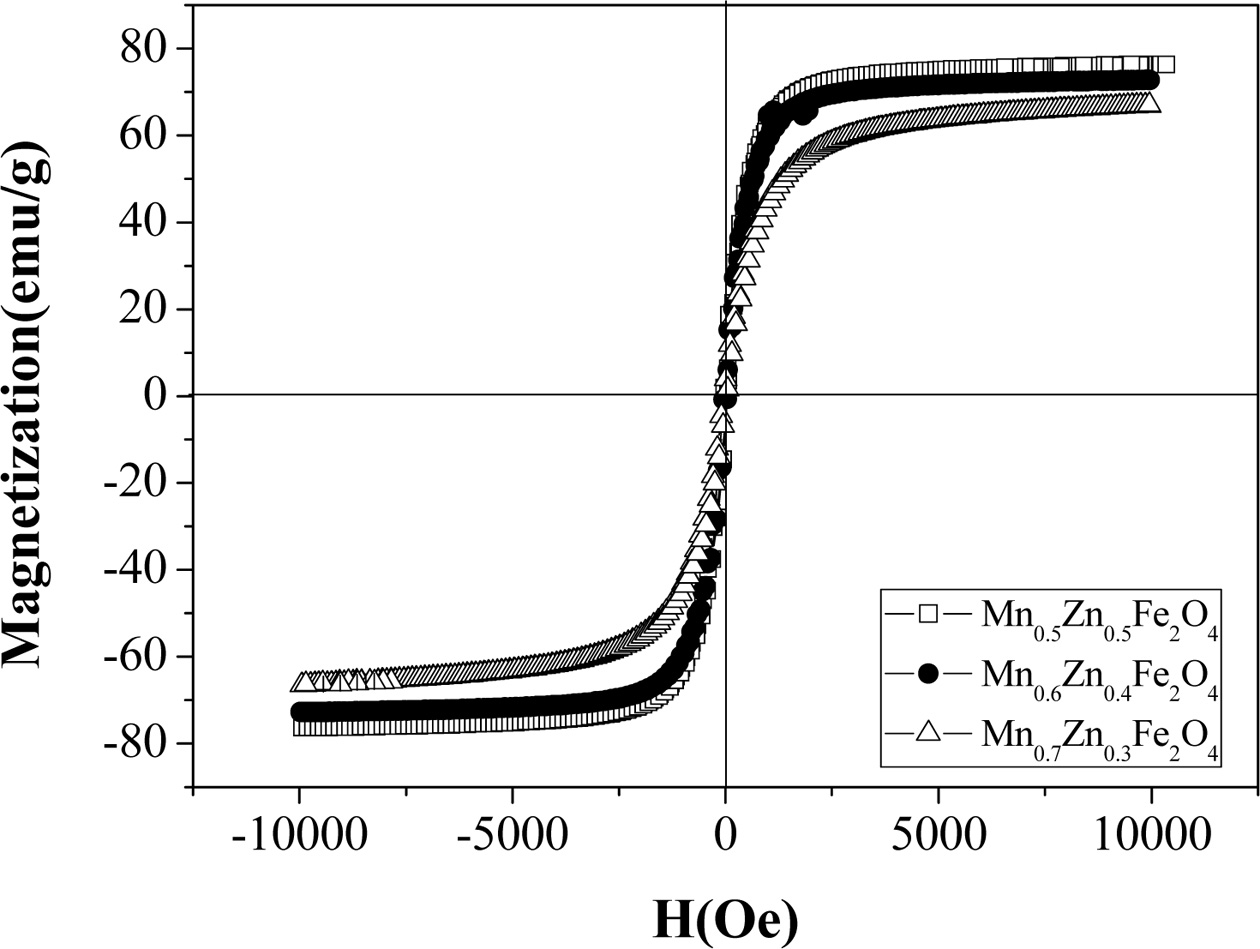
Fig. 5 shows the hysteresis curve of Mn_xZn_1-xFe₂O₄ (x = 0.5, 0.6, 0.7) nanoparticles. As the Mn ion concen-    tration increases from x = 0.5 to 0.7, the saturation magnetization decreases from 76 to 53 emu/g. These magnetization values are thought to be high, which can be derived from a superparamagnetic behavior due to their small particles [32].
The spinel ferrite is cubic and is represented as the general formula AB₂O₄, in which there exist the octahedral and tetrahedral interstitial sites occupied by transition metal cations. Spinel ferrites are classified as a normal spinel or an inverse spinel depending on where cations occupy octahedral sites or tetrahedral sites and can be represented as follows:
 
Me²⁺[Fe₂³⁺]O₄          normal spinel
 
Fe³⁺[Me²⁺Fe³⁺]O₄     inverse spinel
 
Where the ions on the octahedral sites are enclosed in brackets. Normal spinels are formed when Me²⁺ = Zn or Cd, and inverse spinels when Me²⁺ = Ni, Co, Fe, Mn, or Cu. The ferric ion can occupy either tetrahedral or octahedral sites, depending on what other cations are present. The saturation magnetization of ferrite is equal to the difference in sublattice magnetization associated with octahedral and tetrahedral sites. ZnFe₂O₄ is a normal spinel, but MnFe₂O₄ is an inverse spinel. These two compounds form a solid solution Mn_xZn_1-xFe₂O₄ and can be expressed as Zn_1-x²⁺Fe_x³⁺[Mn_x ²⁺Fe_2-x³⁺]O₄, taking into account the site preference of cations. As the Mn content increases at the octahedral site, the number of Fe³⁺ ions at the octahedral site decreases, while the number of Fe³⁺ ions and Zn²⁺ ions at the tetrahedral site increases and decreases, respectively. Zn²⁺ ions have no unpaired electrons, but Mn²⁺ and Fe³⁺ ions each have 5 unpaired electrons. The number of unpaired electrons at the octahedral site is 5x + 5(2 - x) = 10, but the number of unpaired electrons at the tetrahedral site is 0 * (1 - x) + 5 x = 5x. Therefore, the total unpaired electrons are 10 - 5x because the spin directions of the unpaired electrons between the octahedral and the tetrahedral sites are opposite to each other.
As a result, as the Mn content increases, the saturation magnetization is reduced due to the decreased anti-   ferromagnetic coupling, which is well consistent with our results of the saturation magnetization.
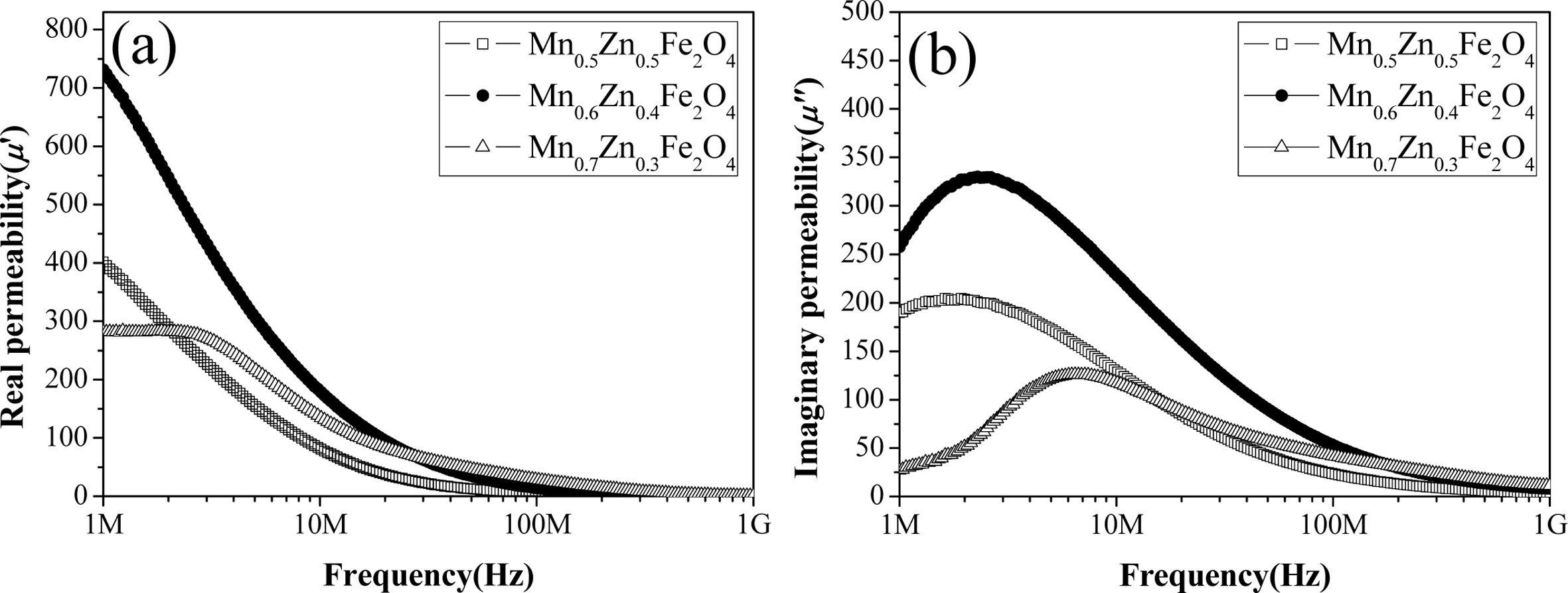
Fig. 6(a)-(c) is FE-SEM images of Mn_xZn_1-xFe₂O₄ (x = 0.5, 0.6, 0.7) samples sintered at 1,250 ^oC in N₂ atmosphere. The grain size is about 3-5 um, but slightly decreased as the Mn content increased. It can be seen that a few large pores presumably due to condensation under observation. Fig. 7(a)-(b) shows the real and imaginary parts of magnetic permeability of Mn_xZn_1-xFe₂O₄ (x = 0.5, 0.6, 0.7) toroidal samples in the frequency range from 1 MHz to 1 GHz. The Mn_0.6Zn_0.4Fe₂O₄ sample exhibits the highest value of about 740 at the real permeability (μ') at 1 MHz of the three composition samples, and its cut-off frequency was 2.36 MHz, which was obtained from the peak point of the imaginary permeability (μ"). The Mn_0.7Zn_0.3Fe₂O₄ sample shows the lowest value of about 285 at the actual permeability (μ') at 1 MHz of the three composition samples, but the highest value at the actual permeability (μ') above 30 MHz, and the cut off frequency is 6.95 MHz.
Since the initial permeability is proportional to the square of the saturation magnetization and reversely proportional to the anisotropy constant and magneto- striction [34]. The observed increase in the initial permeability of the Mn_0.6Zn_0.4Fe₂O₄ sample is believed to be due to an increase in saturation magnetization, as well as a decrease in anisotropy and magnetostriction constants. The Mn_0.7Zn_0.3Fe₂O₄ sample exhibits the largest value at a real permeability (μ') of 30 MHz and above, and can generally be described by two types of magnetization mechanisms: spin rotation and domain wall motion.

Mn_xZn_1-xFe₂O₄ (x = 0.5, 0.6, 0.7) ferrite nanoparticles were well synthesized by a thermal decomposition method and identified as pure spinel ferrite structures by x-ray diffraction analysis. The synthesized ferrite nanoparticles were calculated to be 22.9 nm in diameter by the Scherrer equation, which was well consistent with the particle size of about 25 nm observed from FE-SEM images. The lattice parameters of ferrite nanoparticles monotonously decreased as the Mn content increased. The synthesized ferrite nanoparticles showed the superparamagnetic properties characterized by high saturation magnetization, zero coercivity and remanence. The saturation magnetization value was 76-66 emu/g depending on the Zn content. Toroidal samples were prepared by sintering ferrite nanoparticles at 1,250 ^oC in N₂ atmosphere, and they exhibited faceted grain morphology in FE-SEM images with a grain size of about 3-5 ¥ìm. The real permeability (¥ì') at 1 MHz of the three composition samples, and its cut-off frequency was 2.36 MHz, which was obtained from the peak point of the imaginary permeability (¥ì¡±). The cutoff frequency of the ferrite toroidal sample was about 20 MHz, which seemed to be associated with domain wall resonance.