A series of Ce-doped BaTi_0.97Y_0.03O₃ powder samples with the composition (Ba_1-xCe_x)(Ti_(0.97-x/4)Y_0.03)O₃ (x = 0.00, 0.01, 0.03, 0.05, 0.07 and 0.09) were prepared using the sol gel process and calcined at a relatively low temperature (950°C/4h) and their structural and piezoelectric properties investigated. From structural investigations, it was observed that the samples crystallize in the pseudo cubic phase with the presence of secondary phases for concentrations such as x > 0.03. Piezoelectric parameters were determined and their thermal behavior investigated. The impedance study indicated the dominance of the resistance of the grain boundaries compared to that of grains in BaTi_0.97Y_0.03O₃ sample.

Keywords: Sol gel process, Ce-doped BaTi_0.97Y_0.03O₃, Piezoelectric properties, Complex impedance

Barium Titanate (BaTiO₃), with a perovskite structure of a general formula ABO₃, is one of the ceramic materials that exhibit interesting ferroelectric, dielectric and piezoelectric properties with wide technological applications such as ultrasonic transducers, Multilayer Ceramic (MLCCs), detection of gaseous pollutants like CO, ferroelectric random access memories (FRAM's), Positive temperature coefficient resistors (PTCR), pyroelectric security surveillance systems, IR detectors, etc. [1-5]. Ferroelectric materials form a sub-group of piezoelectric materials. In ABO₃ perovskite materials, piezoelectric properties have been shown to be improved under particular conditions such as near phase transitions [6] or with compositions of ceramics close to the morphotropic phase boundary [7]. Attempts have also been made to enhance these properties through doping [8-14]. Doping BaTiO₃ with rare earth elements was shown to improve its permittivity and to give rise to excellent electrical properties [15]. In particular, it was observed that incorporation of most of RE elements in BaTiO₃ matrix lowered the temperature of the ferro-to-paraelctric phase transition (Curie point) [16], and that these RE elements may occupy Ba or/ and Ti sites depending on their ionic radii. However, the procedure of synthesis has a great influence on this sites occupation property [17, 18]. In ABO₃ structured compounds, A ion is twelve fold coordinated by oxygen ions and B ion is octahedrally coordinated by oxygen ions. The origin of ferroelectricity in BaTiO₃ derives from the displacement of ions relative to each other. BaTiO₃ is a ferroelectric material of which dielectric properties can be modified by chemical substitution of barium and/or titanium by a wide variety of isovalent and aliovalent dopants. In addition to the sintering process, these properties are however greatly influenced by impurities, especially by a donor or an acceptor dopant. It is also known that cerium, which is a donor dopant, occupies the Ba sites in the crystal lattice of BaTiO₃. On the other hand, substitution of Ce³⁺ on Ba²⁺ sites creates charge defects. Doping with Ce have been reported to influence the piezoelectric response of the doped material (BaTiO₃). Brajesh et al. [19] elaborated Ba(Ti, Ce)O₃ samples (Ce³⁺ substitutes Ti⁴⁺ ions in BaTiO₃ matrix) and have observed that the (longitudinal) piezoelectric charge coefficient (d₃₃) increased first, reached its maximum value at 2% in Ce before it decreased.
The aim of the present work is the synthesis, by the sol gel process, and the characterization of BaTi_0.97Y_0.03O₃ and cerium doped BaTi_0.97Y_0.03O₃ materials, in view of investigation of the influence of doping BaTiO₃ material with Ce³⁺ ions at Ba sites on their piezoelectric properties. 

The following precursors were needed to synthesize the series of samples (Ba_1-xCe_x)(Ti_(0.97-x/4)Y_0.03)O₃ (BCYTx): barium acetate trihydrate (Ba(CH₃COO)₂, 3H₂O), titanium isopropropoxide Ti[OCH(CH₃)₂]₄, yttrium (III) acetate hydrate (Y(C₆H₉O₆),H₂O) and Cerium(III) acetate hydrate (Ce(CH₃COO)₃,H₂O). During the preparation process, lactic acid (C₃H₆O₃) was used as peptizing agent. Calcination in air of the raw powders was done in a programmable oven at the temperature of 950 °C for 4 h. For dielectric measurements, uniaxially pressed pellets (of around 1.2 mm thickness and a diameter of around 12 mm) were sintered at 1200 °C for 6 h in a programmable oven. The structural properties of the samples were investigated using an X-ray diffraction diffractometer (XPERT-PRO) with Cu-Kα radiation (λ = 1.54059 Å). The dielectric measurements were carried out in the frequency range 1 kHz to 2 MHz and temperature from ambient to 380 °C using an Agilent 4284A precision impedance analyzer (Hewlett-Packard, Palo Alto, CA).

Structural analysis
The room temperature X-ray diffraction (XRD) patterns of the as-prepared (Ba_1-xCe_x)(Ti_(0.97-x/4)Y_0.03)O₃ samples (BCYTx, x = 0; 1; 3; 5; 7 and 9%), calcined at 950 ºC-4 h (Fig. 1), revealed well resolved peaks corresponding to the pseudo cubic structure with the presence of BaCeO₃ secondary phase (detected at 28.5°) at concentrations in Ce such as x > 0.03.
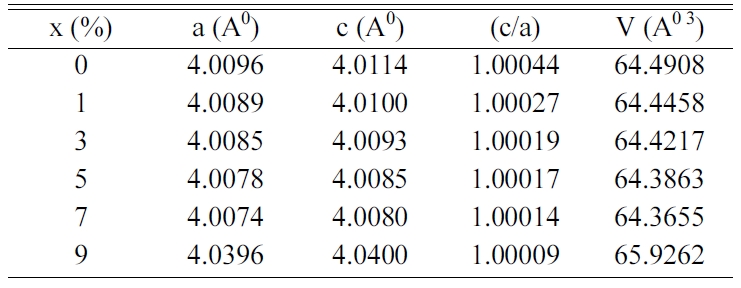
Table 1 gathers the values of the lattice parameters (a, c), the tetragonality (c/a) and the unit cell volume (V) of BCYTx. A substitution of Ba²⁺ ions by Ce³⁺ ones in BaTi_0.97Y_0.03O₃ matrix results in a shrinkage of the volume of the unit cell until 7% in Ce³⁺, because the ionic radius of Ce³⁺(r(Ce³⁺) = 1.34 Å, coordination number (CN) = 12) is smaller than that of Ba²⁺(r(Ba²⁺) = 1.61 Å, CN = 12). Therefore, an expansion of this volume for the concentration x > 0.07 can be ascribed to the occupation of Ce³⁺ ions of Ti-sites as the ionic radius of Ce³⁺(r(Ce³⁺) = 1.01 Å, CN = 6) is larger than that of Ti⁴⁺(r(Ti⁴⁺) = 0.605 Å, CN = 6).
Moreover, doping with Ce gave rise to a shift of the position of the XRD peaks to high values (x < 0.07) (Fig. 1), which reveals a shrinkage of the unit cell (as indicated by the Bragg relation 2d sin(θ) = nλ), and, consequently, a reduction of its volume as illustrated on Fig. 2 displaying the evolutions of the position of the peak (110) and the volume of the unit cell, in conformity with the discussion of the site occupation of Ba given above.
 
Piezoelectric studies
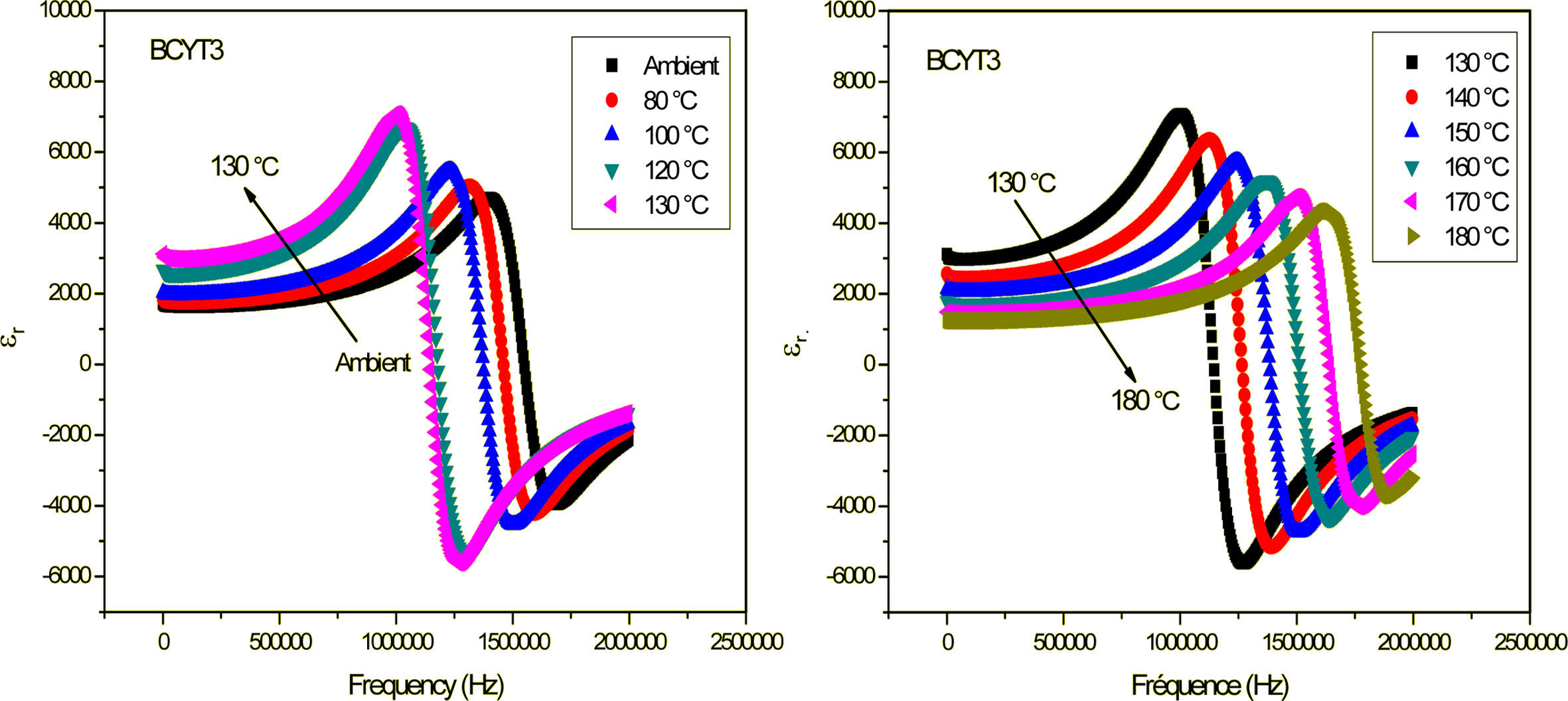
The piezoelectric coefficients were determined using the resonance and anti-resonance frequencies obtained from the variation of the dielectric permittivity with frequency, for each temperature [20], of the BCYTx samples (x = 0; 3; 7 and 9%). Fig. 3 shows as illustration the variation of the dielectric permittivity (ε_r) with frequency of the BCYT3 sample at different temperatures.
The different piezoelectric constants can be expressed as follows.
The planar electromechanical coupling factor K_p:


 
The calculation of the piezoelectric charge constant d^B and the voltage constant g^B at high temperatures was done using the following relations:
 


 
With:
Φ: Diameter of the sample (m)
α^E: The poisson coefficient (0.31 for ceramics)
η: The root of the Bessel equation (η = 2.05)
d: Density (Kg /m³)
ε₀: is the permittivity of free space (8.854*10^-12 F/m)
ε_r: The relative permittivity
f_r : Resonance Frequency (Hz)
f_a : Anti-resonance frequency (Hz)
 
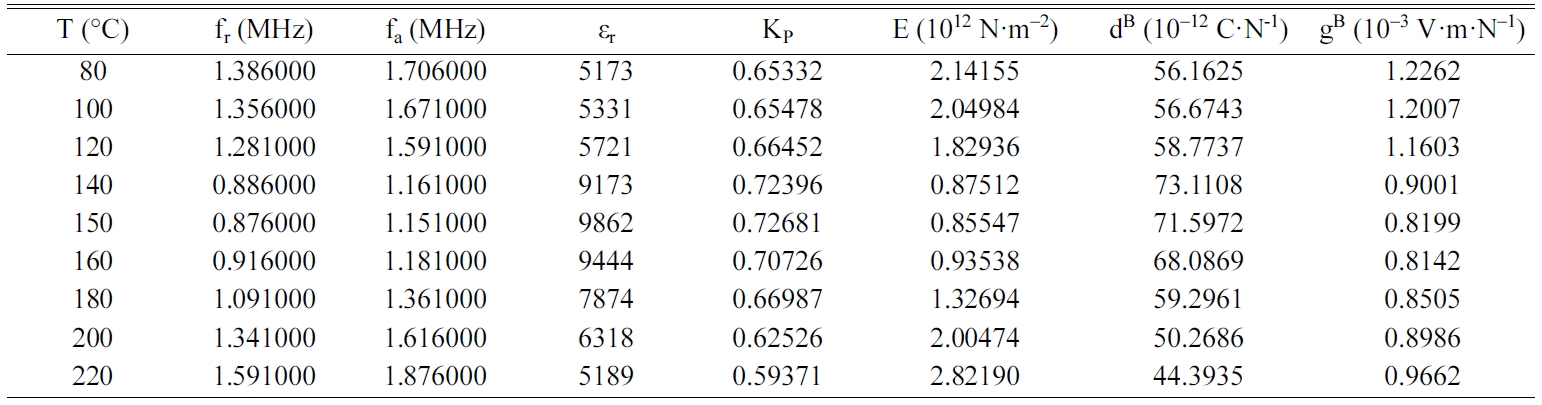
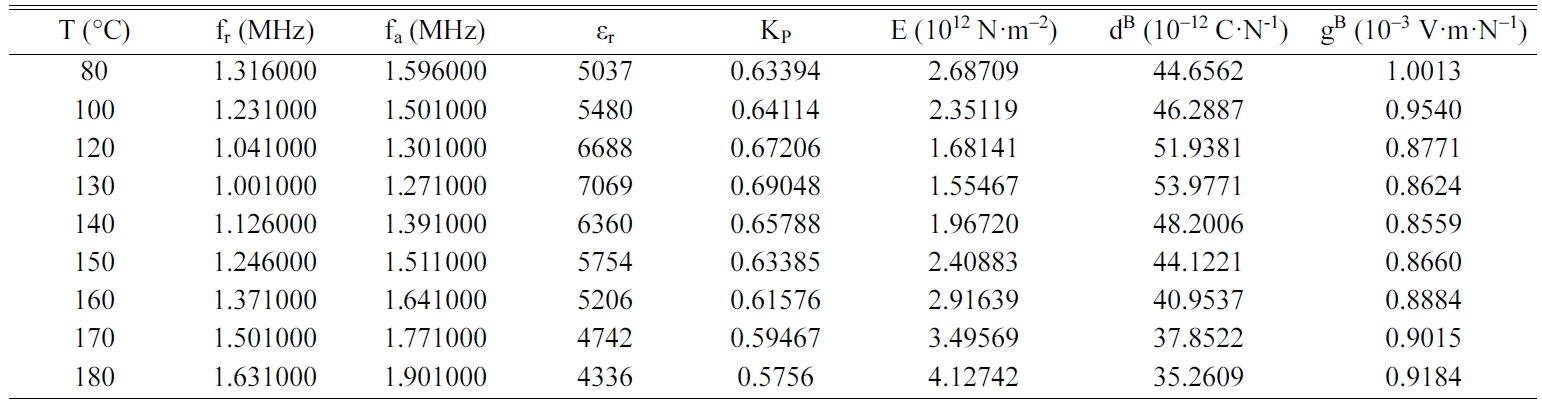
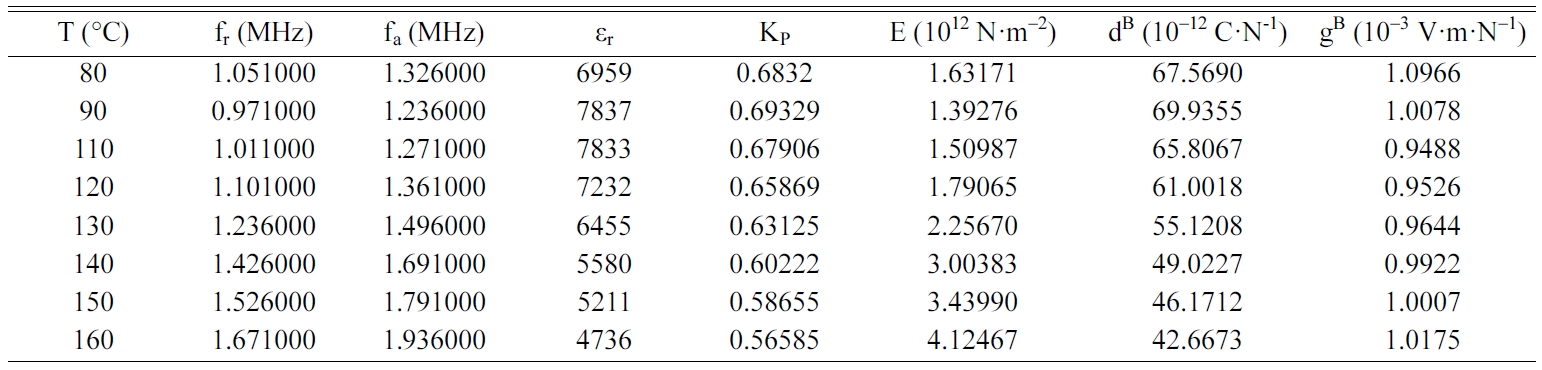
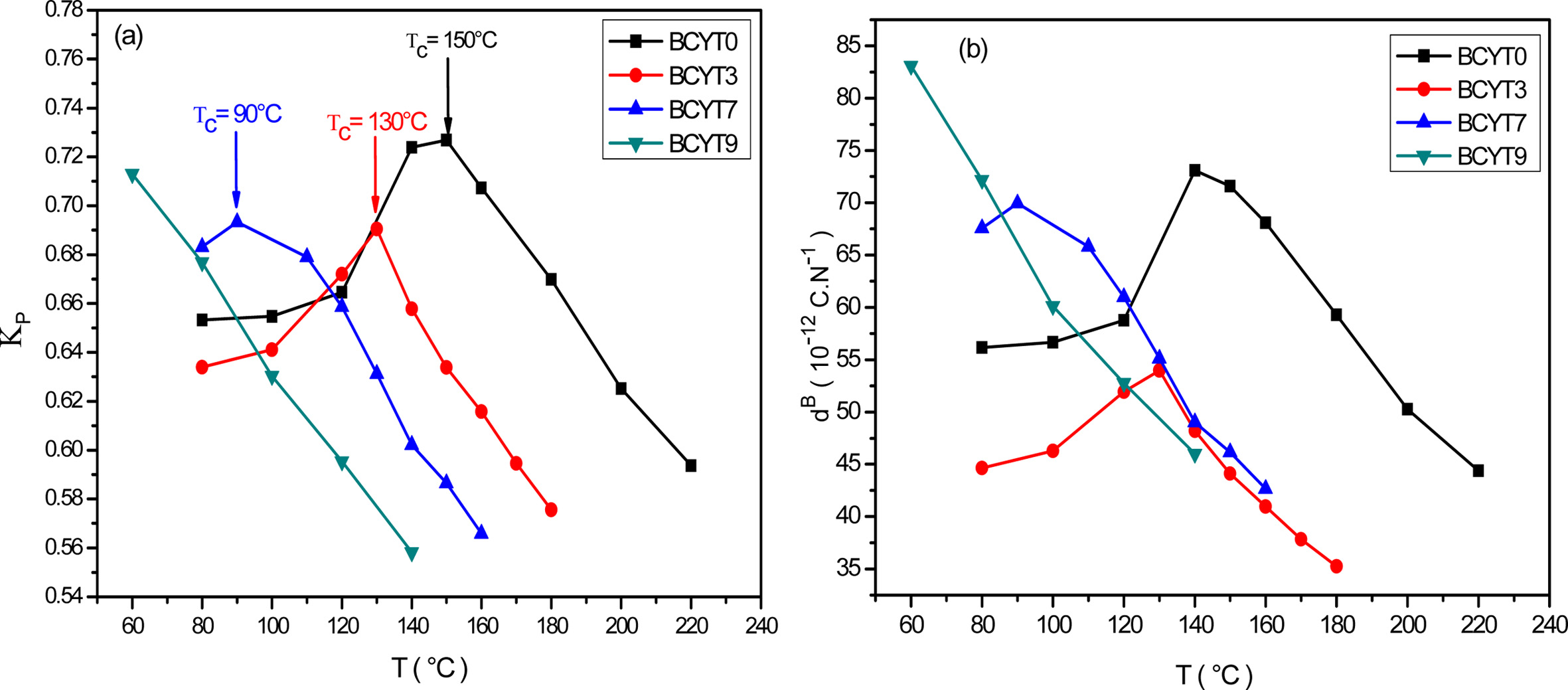
Tables 2, 3, 4 and 5 gather the values of the parameters f_r, f_a, ε_r, K_p, E, d^B and g^B for each temperature of the BCYTx samples (x = 0; 3; 7 and 9%). The planar electromechanical coupling factor, K_p, represents the ability of a ceramic to transform electrical energy into mechanical energy. The values that appear in Tables 2, 3 and 4 show an increasing behavior of this factor with temperature until a maximum around the temperature of the ferro-to-paraelectric transition, T_c, before it decreased (Fig. 4a). It was observed that incorporation of Ce³⁺ led to a decrease of T_c of the sample BaTi_0.97Y_0.03O₃. Sabina et al. [16] prepared Ba_1-xCe_xTiO₃ (0 ≤ x ≤ 0.04) using the conventional solid state reaction method and has found that the T_c was decreased with increasing Ce content.
The piezoelectric charge coefficient d^B (Fig. 4b), has the same variation as K_p; this coefficient reached its maximum value around T_c and then decreased. This decrease may be due to thermal agitation which is responsible of a disorder in the material.
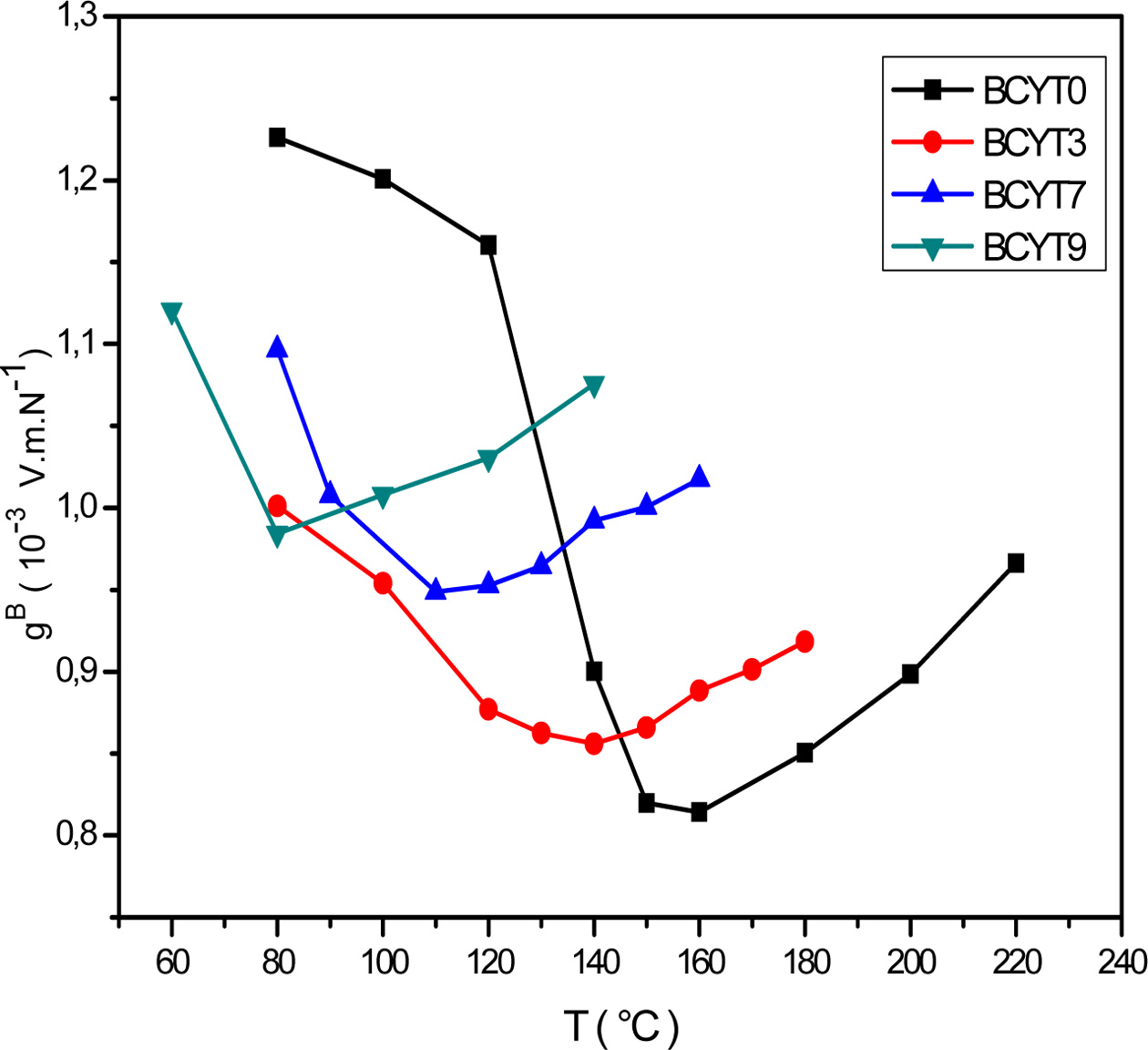
We noticed that the piezoelectric voltage coefficient, g^B, decreased first with increasing temperature and reached its minimum value around T_c and then increased (Fig. 5). It is clear that optimum values of the piezoelectric coefficients are all observed around T_c.
Table 6 compares the obtained values of the piezoelectric parameters for BCYTx samples with some of these constants collected from the literature. Incorporation of Ce did not improve the piezoelectric constants, in particular the piezoelectric charge coefficient. Moreover, lower values of this parameter were recorded compared with those of Brajesh et al. [19] due probably to the presence of Yttrium in our samples.
 
Complex impedance and electrical modulus studies
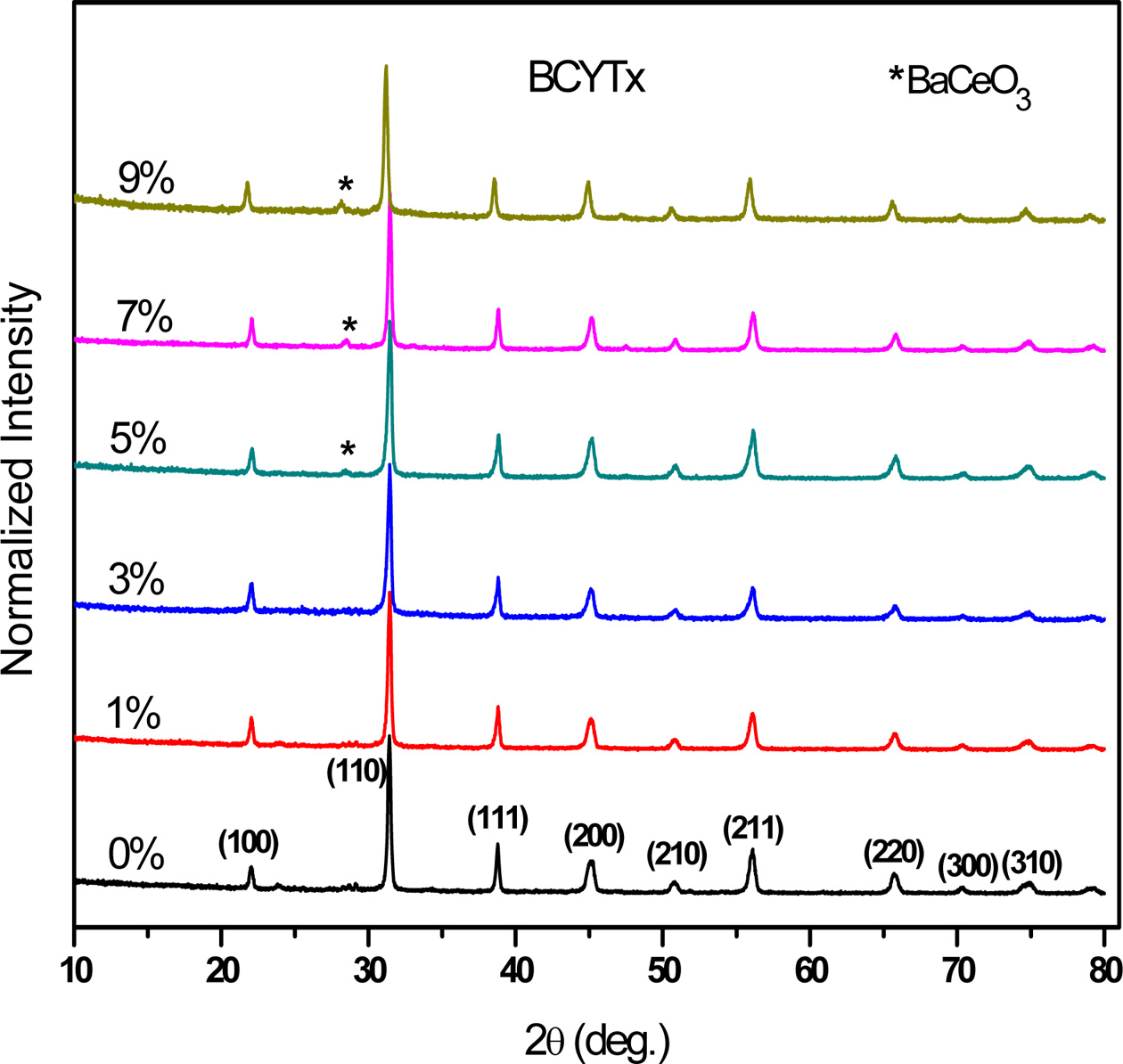
The electrical properties of a material are normally determined from the dielectric data with the help of the following relations: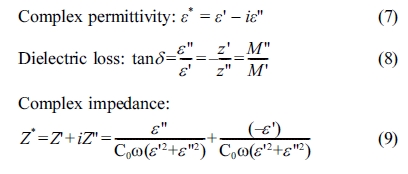


 
Where ω = 2πf is the angular frequency, C₀ is the capacitance of the cell in vacuum, (ε', Z') and (ε'', Z'') are the real and imaginary components of permittivity and impedance, respectively.
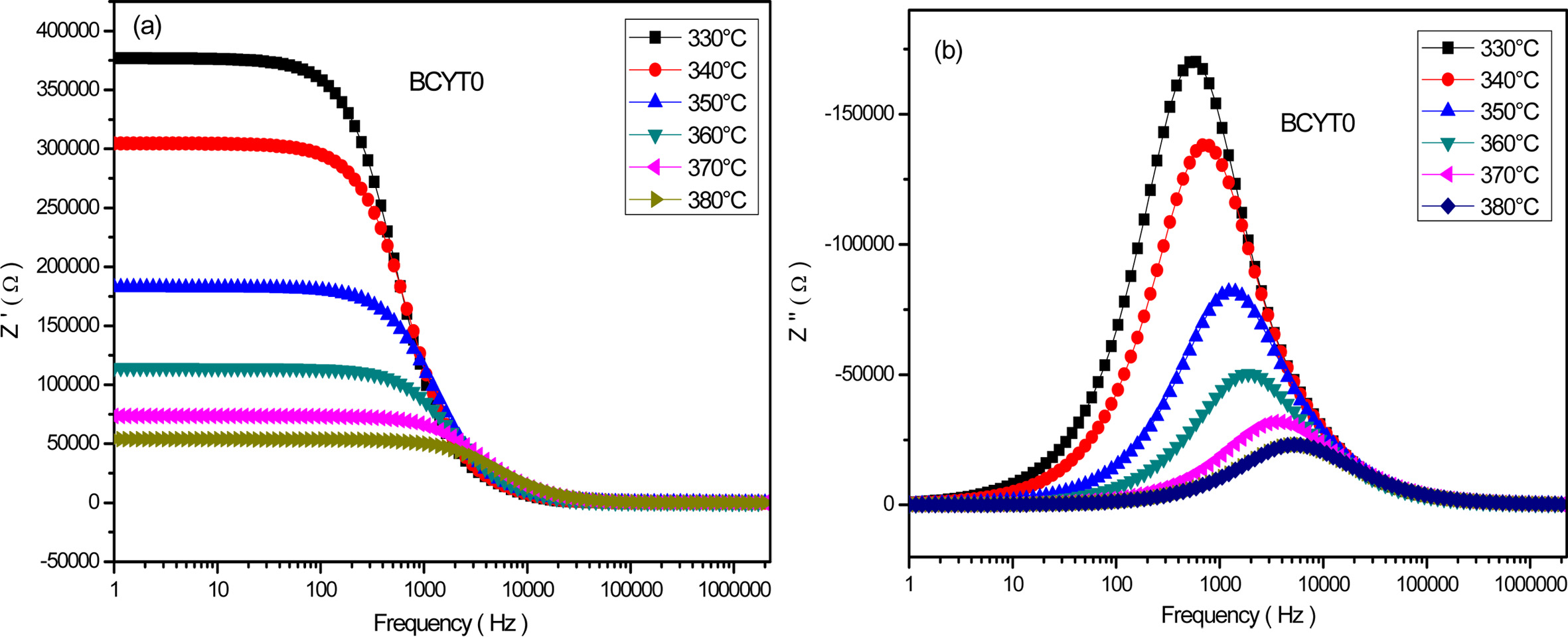
Fig. 6(a) shows the frequency dependence of the real part Z' at different temperatures of the sample BaTi_0.97Y_0.03O₃. This figure shows a decrease of Z' in the low frequency interval with increasing temperature followed by a saturation in the high frequency region. This indicates the presence at low frequency of all types of polarisation mechanisms in the sample. Fig. 6(b) displays the frequency dependence of the imaginary part of Z'' at different tempertures of the sample BCYT0, and shows first an increase of this parameter with frequency before reaching a maximum that shifts to the high frequency region with increasing temperature and then decreases to an almost quasi constant value. The broadening of the peaks indicates a possible distribution of relaxation times.
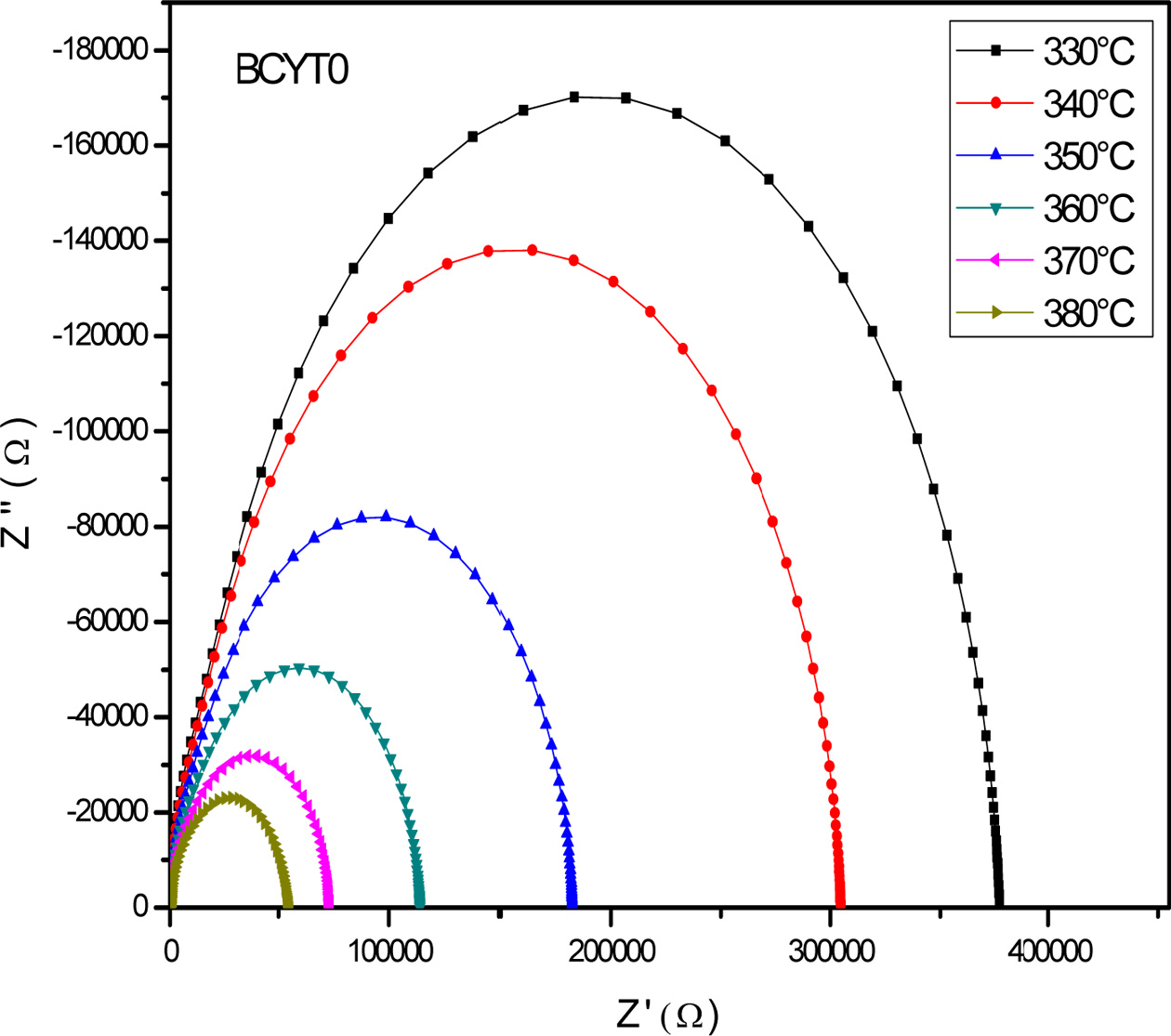
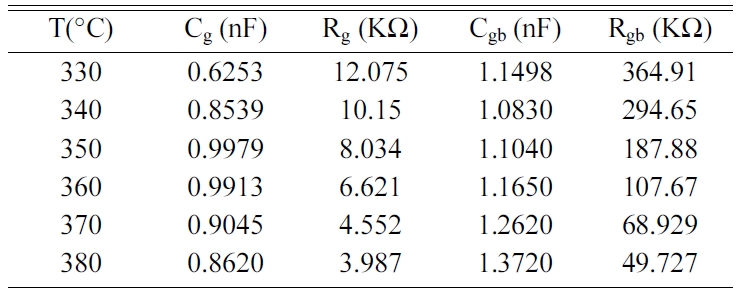
Fig. 7 displays the Nyquist diagram of BCYT0 at different temperatures, which consisted in half circles that are dominated by the grain boundaries resistance R_gb. Indeed, grain resistance (R_g) is very weak compared to that of the grain boundaries, as revealed by their values gathered in Table 7. The grain boundaries and grains effects were each modeled by a constant phase element parallel to a resistance.
El Ghandouri et al. [23] in their dielectric study of Ba_1-xLa_xTi_(1-x/4)O₃ (0 ≤ x ≤ 0.4) samples obtained similar results pointing out the strong effect of grain boundaries on the conduction mechanism in these compounds.
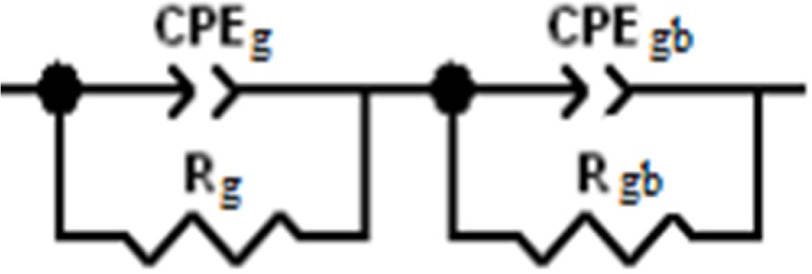
By adjusting our experimental data with the help of the equivalent circuit of Fig. 8, values of the capacitance and the resistance of grains (C_g, R_g) and grain boundaries (C_gb, R_gb) were determined using Z view software and given in Table 7.
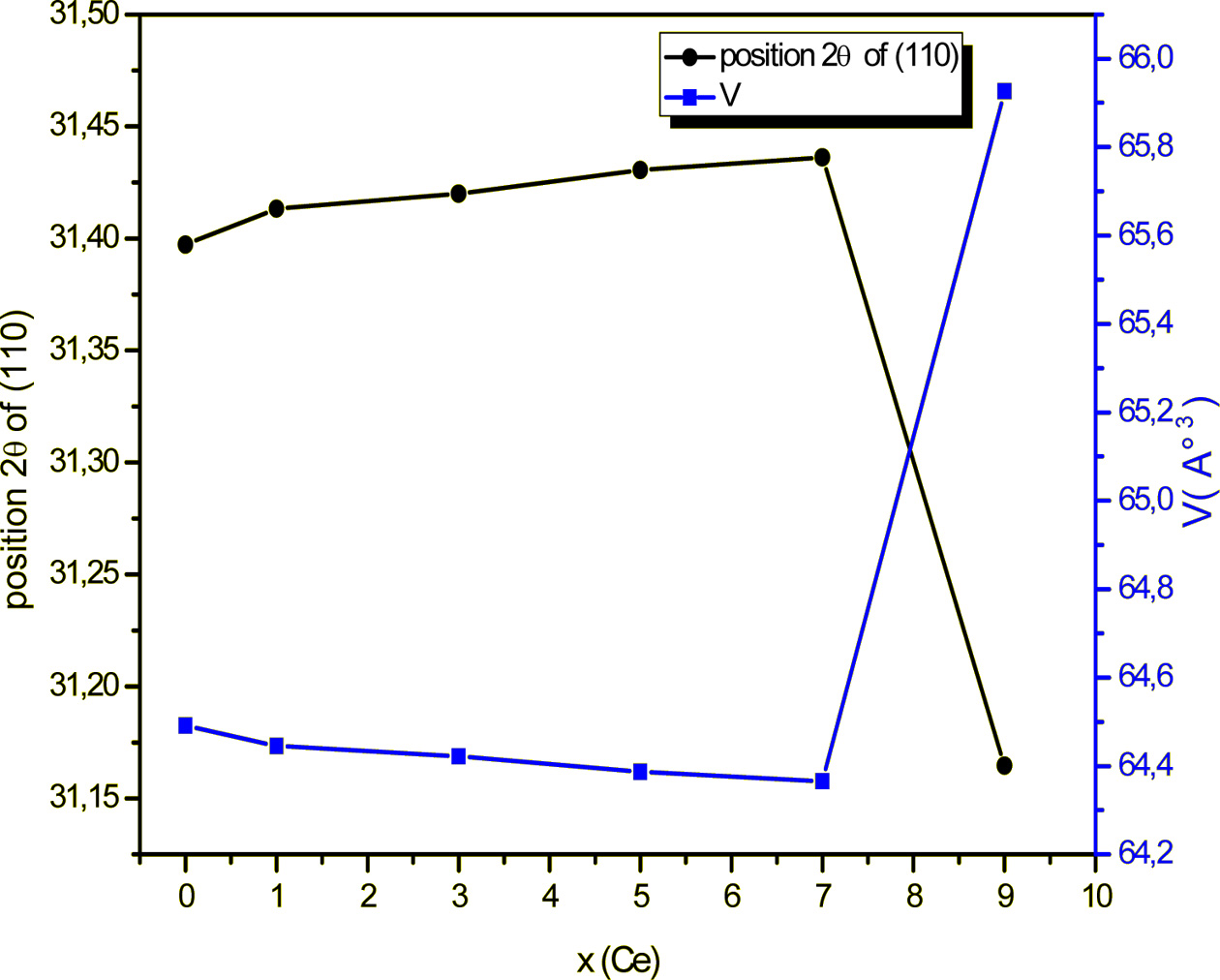
The complex electrical modulus (M*) is defined as a function of the complex dielectric permittivity (ε*) by the following relation:
 

 
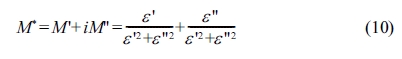
Where M' and M" are the real and imaginary parts of the complex electric modulus M*, respectively.
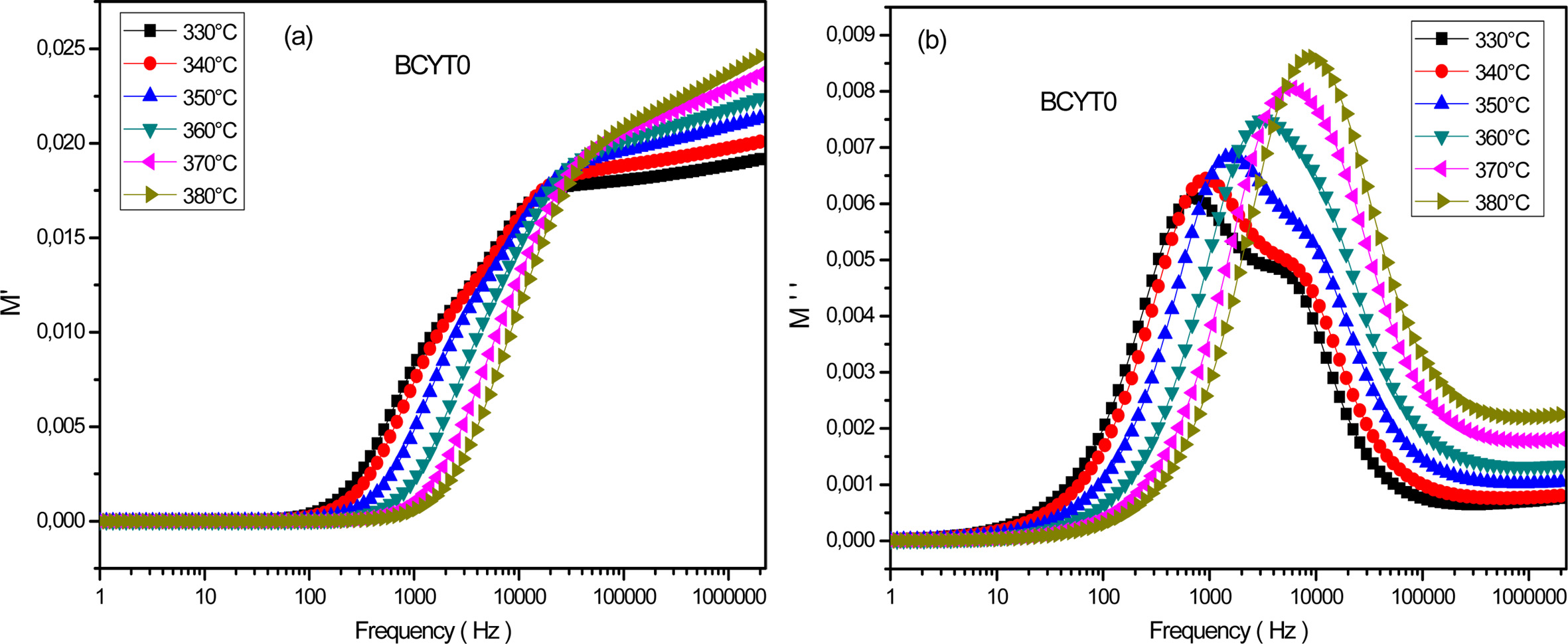
Fig. 9(a) displays the frequency dependence of the real part of M' determined at different temperatures for the sample BCYT0. This figure showed a very weak value of M' at low frequencies followed by a dispersion with increasing frequency and reached a finite limit that increased with increasing temperature. The latter behavior may be due to the mobility at short distances of charge carriers [24]. Fig. 9(b) displays the frequency dependence of the imaginary part M'' at different temperatures of the sample BCYT0. This figure showed that M'' increased with increasing frequency, passed through a maximum which moved towards high frequency region and which magnitude increased with temperature. This behavior suggests a thermal activated relaxation process [24].  Table 2 Table 3 Table 4 Table 5

Ce-doped BaTi_0.97Y_0.03O₃ ceramics were successfully prepared and their piezoelectric and impedance constants determined from resonance and antiresonance values given by dielectric measurements. Structural analysis showed that Ce³⁺ ions occupied Ba sites until x = 0.07 and then incorporated Ti sites indicating that the concentration 0.07 represents a solubility limit in BaTi_0.97Y_0.03O₃. It was also observed that in the presence of Yttrium and in the range of concentrations in Ce studied, the mechanism of conduction is strongly affected and dominated by grain boundaries. Moreover, the incorporation of Ce did not enhance the piezoelectric parameters compared to some published ones. More work is needed to clarify the role of Y atoms and site occupation of Ce atoms in inhibiting the piezoelectric constants.