FeVSb_1-xTe_x (0.02 ≤ x ≤ 0.10) half-Heusler alloys were fabricated by mechanical alloying process and subsequent vacuum hot pressing. Near single half-Heusler phases are formed in vacuum hot pressed samples but a second phase of FeSb₂ couldn’t be avoided. After doping, the lattice thermal conductivity in the system was shown to decrease with increasing Te concentration and with increasing temperature. The lowest thermal conductivity was achieved for FeVSb_0.94Te_0.06 sample at about 657 K. This considerable reduction of thermal conductivities is attributed to the increased phonon scattering enhanced by defect structure, which is formed by doping of Te at Sb site. The phonon scattering might also increase at grain boundaries due to the formation of fine grain structure. The Seebeck coefficient increased considerably as well, consequently optimizing the thermoelectric figure of merit to a peak value of ~0.24 for FeVSb_0.94Te_0.06. Thermoelectric properties of various Te concentrations were investigated in the temperature range of around 300~973 K.

Keywords: Thermoelectric, Thermal conductivity, Seebeck coefficient, Thermolectric figure of merit

Fossil fuel, the main source of energy today, is finishing up very quickly. Thus, the energy scientists are giving priority to alternative energy sources before the fossil fuels deposit run out. Moreover, fossil fuels are spreading various greenhouse gases, which are the main cause of global warming. A sustainable supply of clean energy is now in demand for future energy solution. It is noted that, a lot of energy is wasted in the form of heat during energy utilization process. Thermoelectric (TE) power generators could be a possible solution because this can transform the waste heat into useful electrical energy [1-3]. The efficiency of a thermoelectric material is calculated by the dimensionless figure of merit, ZT = S²sT/(k_l + k_e), where S is the Seebeck coefficient, σ is the electrical conductivity, T is the temperature, k_l is the lattice thermal conductivity, and k_e is the thermal conductivity due to electrons.
FeVSb half-Heusler (HH) materials are getting considerable interest as potential TE materials due to its high power of conversion efficiency and low cost of the elements [4]. In recent times, Fu et al. [5] and Zou et al. [6] reported that FeVSb HH matrix can exhibit both n- and p-type TE properties. Their studies suggest that large power factors could be achieved, though high thermal conductivity limits the TE figure of merit. They proposed that one of the effective ways to get high TE efficiency would be nanostructuring. Nano-structuring produced ZT > 1.2 for n-type MNiSn_1-xSb_x [7-9] and ZT = 0.9~1.0 for p-type MCoSb_1-xSn_x [10, 11], where M = Ti, Zr and Hf. TE figure of merit also can be upgraded by isoelectronic alloying, which is capable of initiating phonon scattering [12]. There is strong evidence which shows that increasing phonon scattering lowers the thermal conductivity considerably [13, 14]. Solubility limits of the forming systems can also be a factor which may bring ‘natural’ nanostructuring into the crystal system. This nanostructuring is also capable of lowering the thermal conductivity [9, 11]. TE efficiency can also be optimized by chemical substitution, which may further improve the power factor of the material system. Doping with electron donating or accepting elements might help to optimize the carrier concentration [15]. Generally, doping establishes point defects in the host matrix, which is innate in any material system. Doping elements act here as an exchange corner between the distant reservoir and the host matrix which could minimize the formation energy of defect into the matrix by controlling the doping limits.
Mechanical alloying process is a well-known high energy milling technique that can produce ultrafine microstructures [16]. It has advantages over other traditional processes such as casting and forging [17, 18]. It may help to produce alloys which are difficult to produce applying conventional metallurgical techniques. MA produces fine-grained particles which improves the TE conversion efficiency by the reduction of lattice thermal conductivity [19]. Fine-grained particles also help to lower the diffusion path to enhance phase transformation and homogenization. The high temperature process such as arc-melting and levitation-melting were avoided to get rid of evaporation of high vapor pressure elements (i.e., Sb, Sn) during processing.
In this study, TE performance of Te-doped FeVSb HH alloys were described as a function of temperature at around 300~973 K. A group of FeVSb_1-xTe_x (0.02 £ x £ 0.10) HH materials was synthesized by mechanical alloying (MA) process followed by vacuum hot pressing (VHP). TE properties were examined in the forms of Seebeck coefficient, electrical conductivity and thermal conductivity. Transport properties were also investigated in terms of Hall mobility, Hall coefficient and carrier concentration.

For the synthesis of FeVSb_1-xTe_x (0.02 £ x £ 0.10) HH alloys, elemental powder mixtures of Fe (99.9%, 63 µm), V (99.9%, 75 µm), Te (99.9%, 53 µm) and Sb (99.9%, 45 µm) were used. A zirconia vial was used to carry out the MA process using a high-energy vibrator mill (KMTech TMM 70, Korea) for 16 h. The milling speed was kept constant at 1,080 rpm in this experiment. 5 mm zirconia balls were used in this process, keeping the ball-to-powder mixture ratio at 10꞉1. Consolidation of the powders was done in VHP for 2 h under the pressure and temperature of 80 MPa and 1,073 K. A 10 mm graphite die was used in VHP for consolidation of powders. Contamination during handling and processing of samples throughout the process was avoided using Ar atmosphere.
A particle size analyzer (PSA) (Horriba LA-950, Japan) was utilized to measure the particle size. X-ray diffraction (XRD; Bruker AXS Advance D-8, Germany) of the MAed and VHPed samples were carried out using Cu (Kα) radiation. The microstructure was investigated using a scanning electron microscopy (SEM) (FEI Quanta-400, Netherland). The Seebeck coefficient and electrical conductivity were measured using ZEM3 (Ulvac-Riko, Japan) by 4-probe method. 3×3×10 mm³ VHPed samples were used for the Seebeck coefficient and electrical conductivity measurements and 10Φ × 1 mm samples were used for thermal conductivity measurement. Thermal diffusivity was captured using TC-9000H (Ulvac-Riko, Japan) by a laser flash method. Density calculation was done by the Archimedes principle. The Van der Pauw method (modified Keithley 7065, USA) was applied to measure Hall measurement.

As-MAed powders are shown to be near spherical shape as in typical MA process, and approximated particle sizes are of less than 10 µm as shown in Fig. 1. Average particle sizes were measured using PSA are 7.0 µm, 6.2 µm, 5.9 µm, 5.3 µm and 5.2 µm for doping concentration, x = 0.02~0.10, respectively. Particle size seems to decrease with increasing doping concentration. The collision of balls to the powder mixture might introduce lattice distortions which could limit the particle size [20].
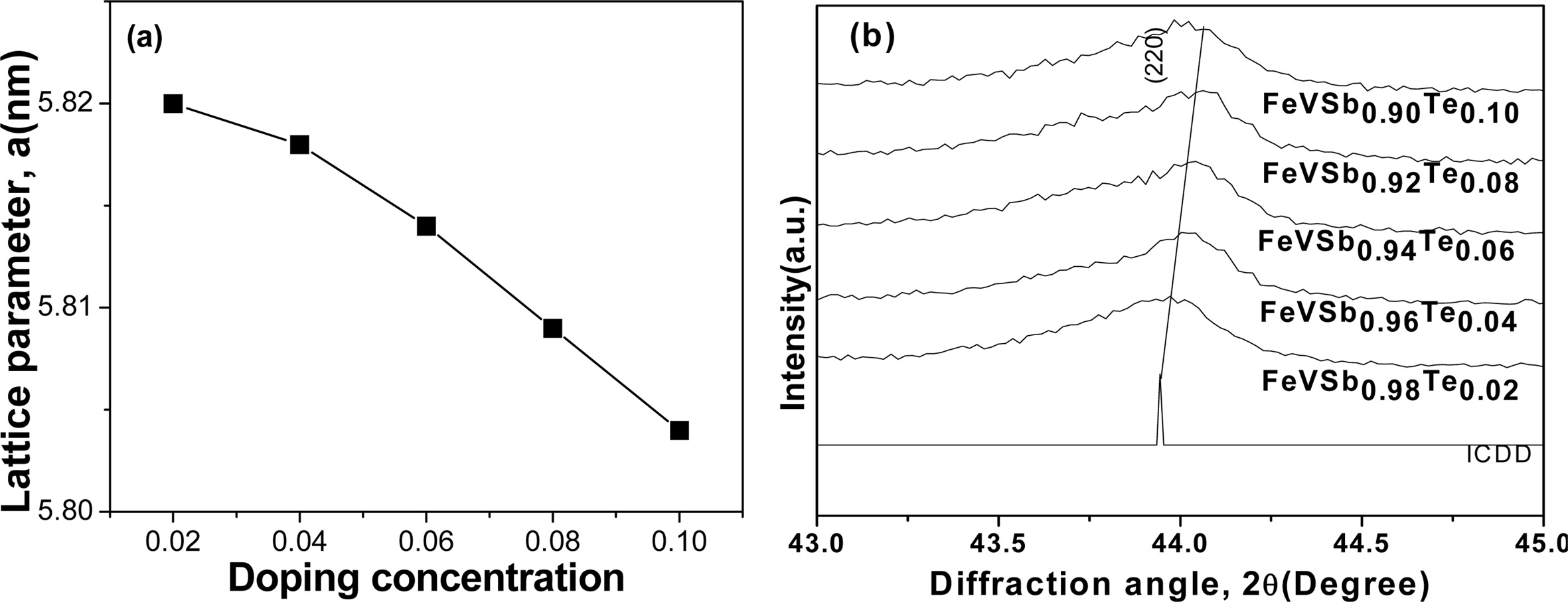
The lattice parameter decreased with increasing doping elements according to Vegard’s law, which stated that lattice parameter varies linearly with the atomic radii of the doping elements [21], as shown in Fig. 2(a). As the atomic size of the dopant decreased, the size of the lattice also decreased. This decrease in lattice parameter might shift the diffraction peak to the longer diffraction angle, which is represented by (220) peak in Fig. 2(b). It is perhaps due to the replacement of larger Sb (atomic radius = 1.45 Å) by smaller Te (atomic radius = 1.35 Å) atom shifts the peak to the longer diffraction angle [22].
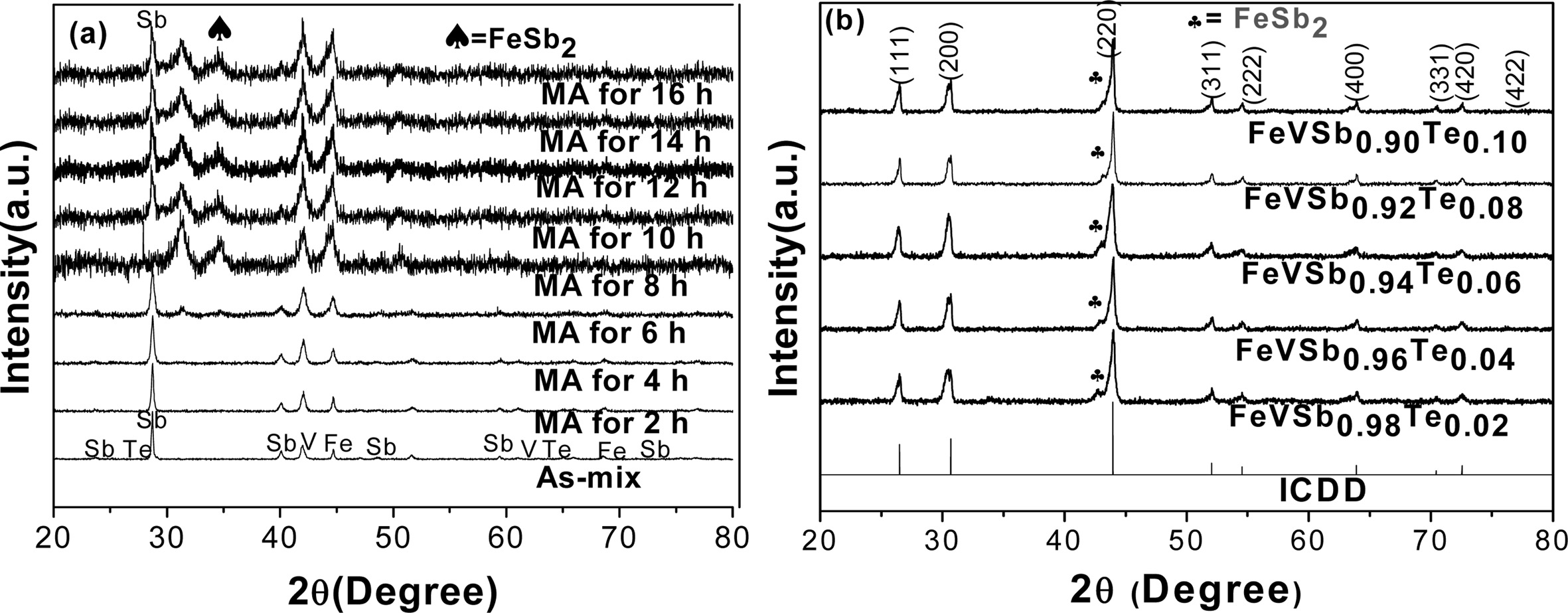
XRD patterns of the as-MAed powders are plotted in Fig. 3(a). The XRD patterns indicated that substitution of Sb by Te took place slowly in FeVSb_1-xTe_x and the HH phase formation progressed during milling. Second phases of FeSb₂and elemental Sb were formed in the as-milled powder. The elemental peak of Sb is completely disappeared but a trace of FeSb₂ is still remained after VHP, which is shown by Fig. 3(b). All the VHPed samples contained HH phases as a dominant phase.
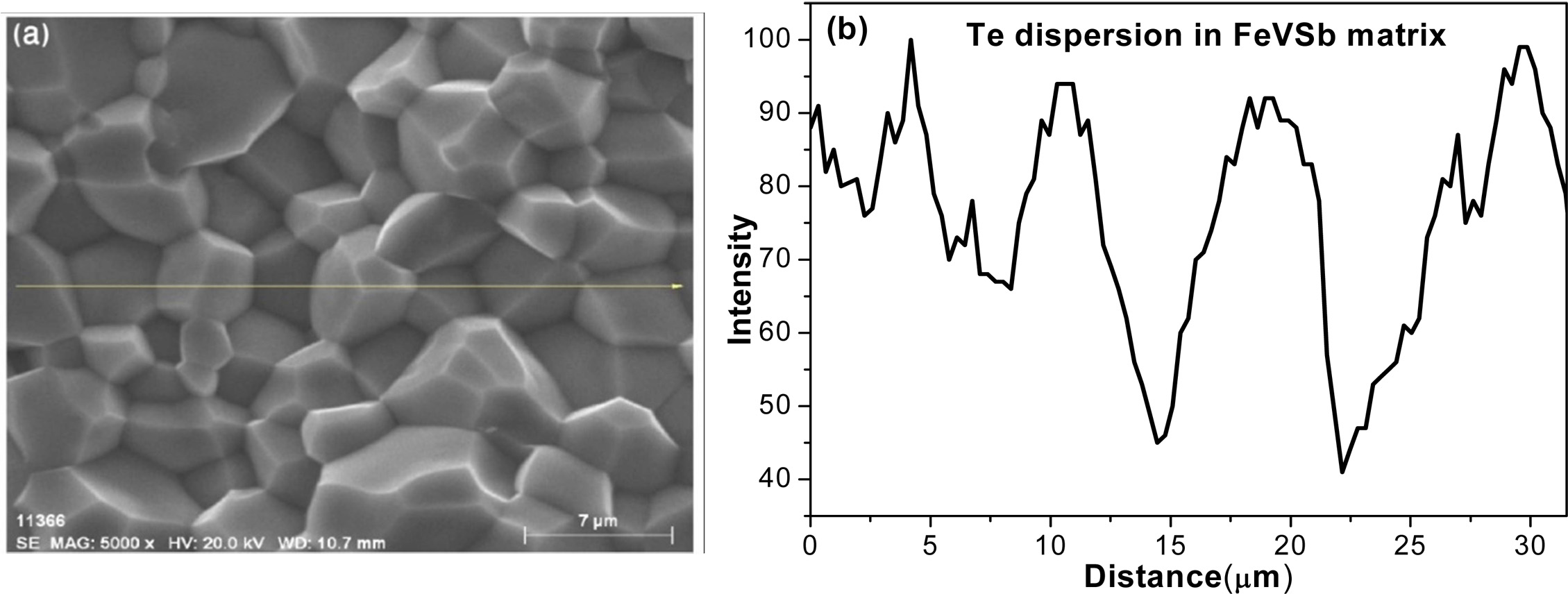
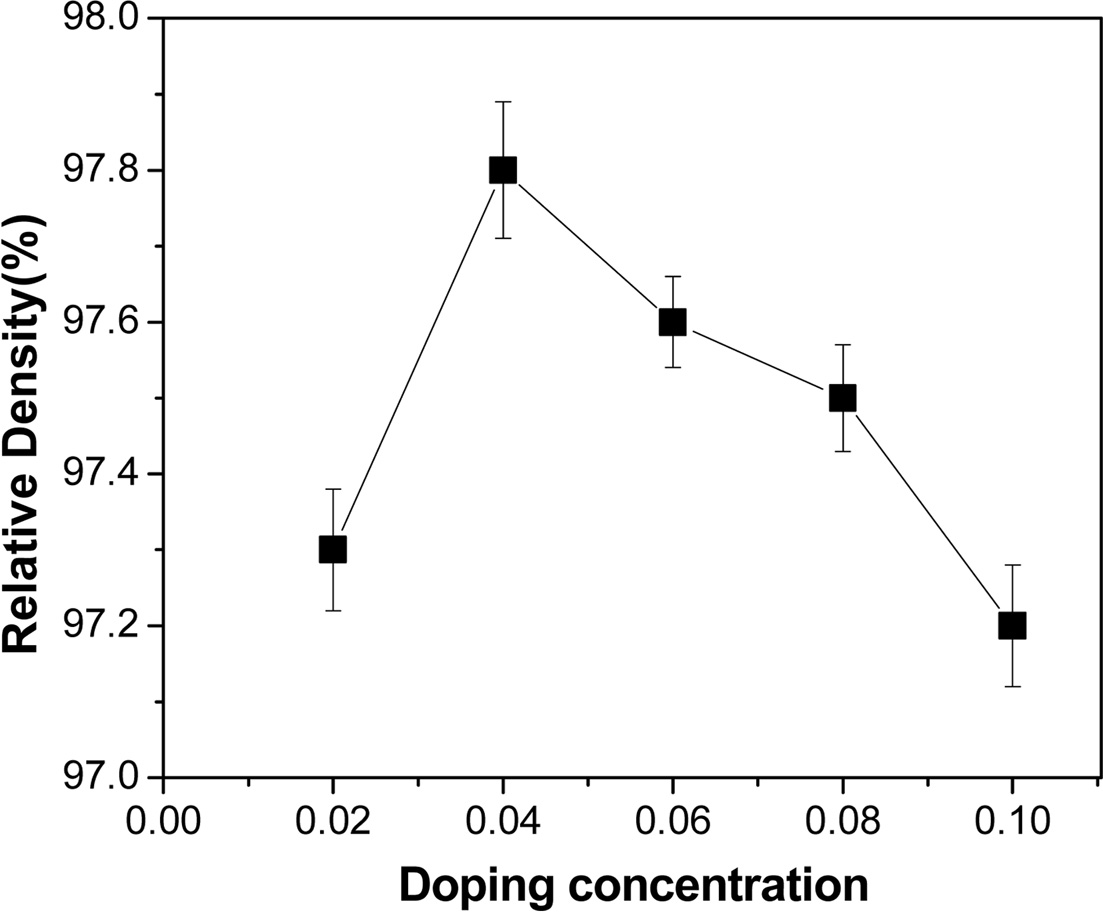
Fig. 4. shows the SEM images of the VHPed samples. Relative density of the VHPed samples is found to be around 98% (Fig. 5.). The grains seem to be densely packed, which could be induced from the relatively high density of VHPed samples. The grain size of the sample measured was found to be less than 10 µm.
Te is a low melting point element (meltingpoint-723 K, boiling point-1261 K). It could be sublimated during VHP process over the melting point temperature. However, sublimation was not much in this measurement. EDS line mapping was performed to find out the traces of Te after VHP. The EDS line mapping of the sample showed that Te was homogeneously dispersed throughout the HH matrix (Fig. 6).
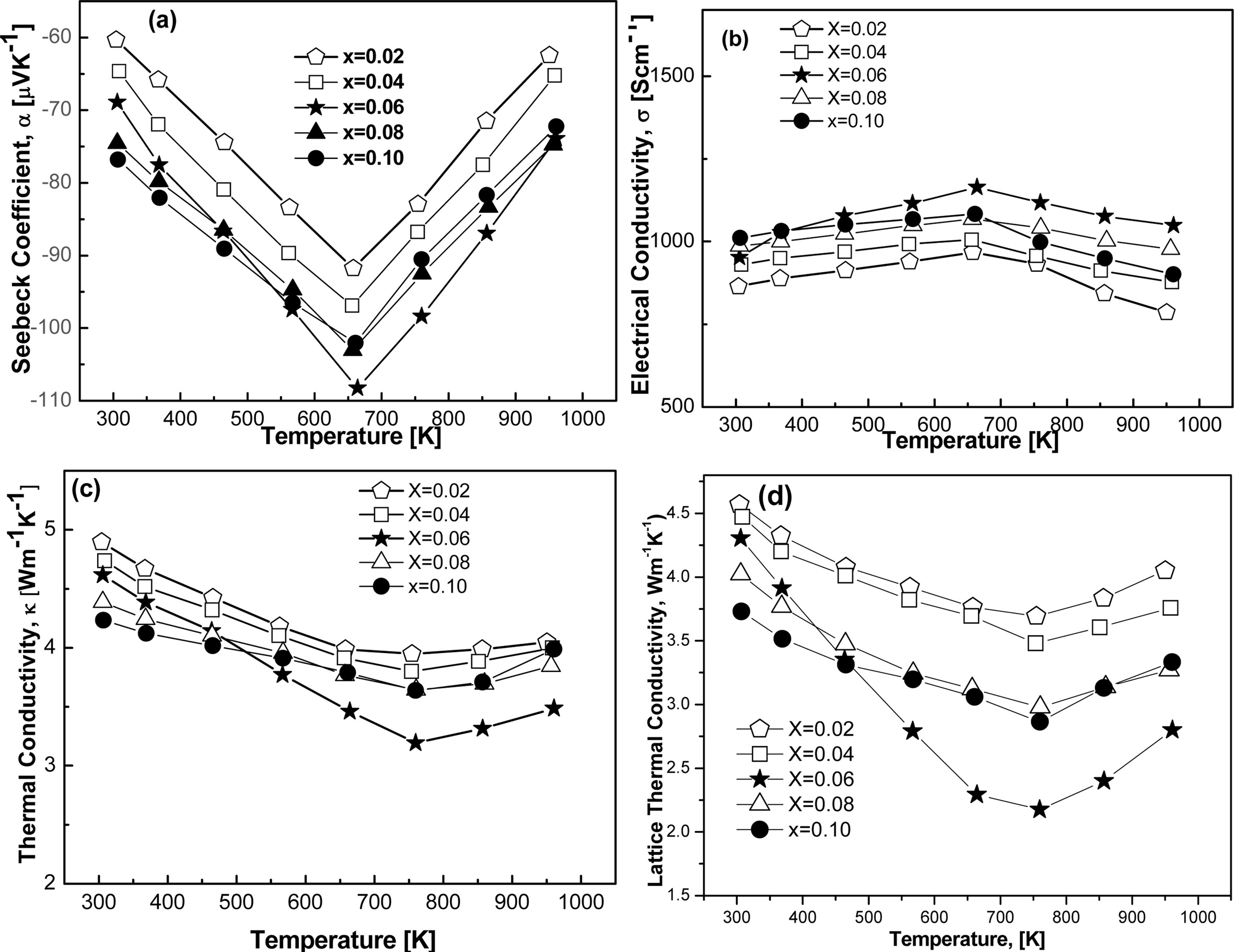
Fig. 7(a~d) shows the temperature dependence of Seebeck coefficient, electrical conductivity, lattice thermal conductivity and thermal conductivity, respectively. Fig. 7(a) reveals that Seebeck coefficient is strongly dependent on Te concentration as it is varied with increasing or decreasing temperature. The charge carriers for the current system turned out to be electrons because the sign of the Seebeck coefficient was found to be negative as can be seen in Fig. 7(a). The absolute value of the Seebeck coefficient slightly increases with increasing Te concentration at room temperature, reaching a maximum value of 77 µVK^-1 for x = 0.06. The absolute value of Seebeck coefficient is increased with the rise of temperature up to 650 K. This gradual increase of absolute Seebeck coefficient could be due to the increase of effective mass of the charge carriers. 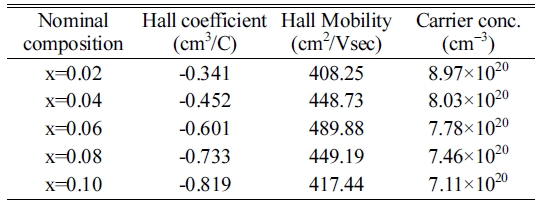As it is established that Seebeck coefficient is directly proportional to the carriers effective mass (S∞m*). Moreover, carrier concentration slightly decreased with the increasing concentration of Te contents as shown in Table 2, which also enhances the Seebeck coefficient as well. FeVSb_0.94Te_0.06 showed strong temperature dependence of the Seebeck coefficient. A maximum value of absolute Seebeck coefficient was found to be 107 µVK^-1 for x = 0.06 at 658 K. This suggests that the composition, FeVSb_0.94Te_0.06 holds great promise for enhanced figure of merit as the Seebeck coefficient and electrical conductivity can be further increased via the optimization of appropriate elemental doping at the Fe/V sites in the system [23]. No incorporation of trace elements during milling was found which is visualized in Table 1.
Temperature dependence of electrical conductivities in FeVSb_1-xTe_x HH samples are demonstrated by the Fig. 7(b). At room temperature, electrical conductivity of all the samples climbed owing to the semi-metallic behavior, which was resulted by the narrow band gap semiconductor [24, 25]. Electrical conductivity increased again for all the samples with the increasing temperature, which indicated metallic behavior. This dependence of the electrical conductivity on increasing Te concentration might be due to the change of carrier concentration and mobility as a function of Te concentration. The highest electrical conductivity of 1,164 Scm^-1 was observed for the sample x=0.06, which also showed the considerable TE efficiency as TE efficiency is directly proportional to electrical conductivity and the degeneracy of electron band. This increase in electrical conductivity could also be due to the easy transformation of Fermi band to the higher conduction band by thermal elevation of electrons within the band gap [26]. Eventually, electrical conductivity slightly decreased at higher temperature range of around 660~973 K. It can be considered that all the samples displayed bipolar electrical behavior over the temperature range of 300~973 K. Although a significant improvement of the electrical conductivity of FeVSb_1-xTe_x alloys could be achieved by optimizing the Te concentration, the observed values are still low for the expectation in TE material. Generally, to be used in a device, ZT of a TE material should be ~1. However, the prospect of further enhancement of the electrical conductivity of this family of compounds is expected to be high through doping on Fe or V sites [26].
Temperature dependence of thermal conductivity and lattice thermal conductivity are shown in Fig. 7(c, d). Both of them markedly decreased at room temperature after adding increasing order of dopants. The lattice thermal conductivity of FeVSb_1-xTe_x decreased considerably with increasing Te contents. It could be due to the enhanced phonon scattering. Possibly, effective hybridization of 5p orbitals of both the Sb and Te optimized the carrier concentration [27]. This optimized concentration increased the effective mass of the carriers, which took part in effective phonon scattering process. In addition, because of the expected small grain size (≤10 μm) of the synthesized FeVSb_1-xTe_xHH materials, a high density of grain boundaries might form. This translates enhanced phonon scattering at grain boundaries which may contribute significantly to the reduction of the lattice thermal conductivity as well. Regardless of the composition, the lattice thermal conductivity decreases considerably with rising temperature (Fig. 7(d)) and lattice thermal conductivity as low as 2.22 Wm^-1K^-1 was achieved at 773 K for composition with x = 0.06. A similar trend was observed for the total thermal conductivity of all FeVSb_1-xTe_x compounds (Fig. 7(c)). 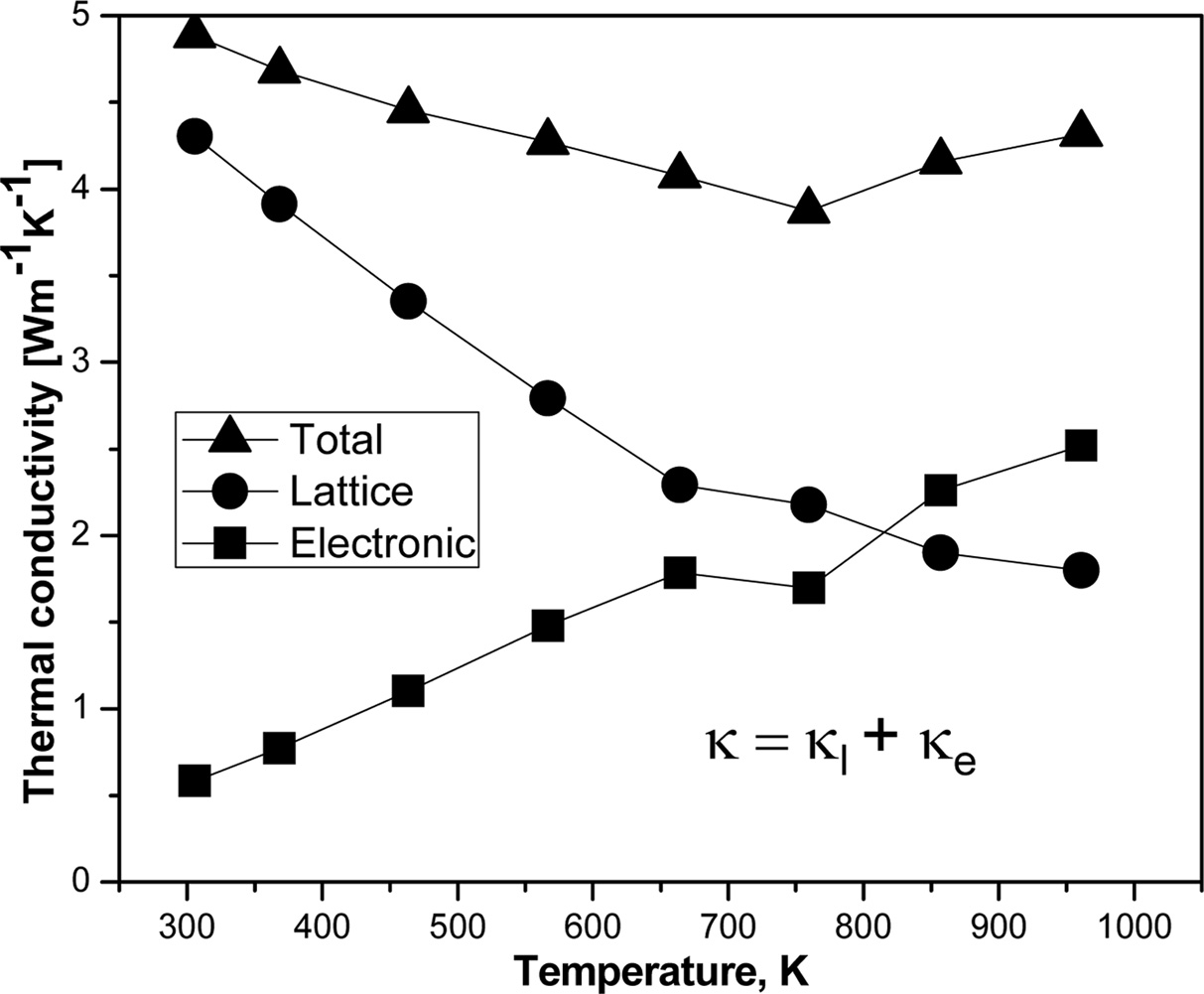There is a marginal difference between the total thermal conductivity and the lattice contribution and is observed for all the compositions due to the very low electronic thermal conductivity of FeVSb_1-xTe_x alloys (Fig. 8). No foreign elements effect on thermal conductivity was observed, which was confirmed by EDS analysis given in Table 1. The electronic thermal conductivity is found considerably low; however, it cannot be ignored for good TE devices. The maximum thermal conductivity is found to be ~5 Wm^-1K^-1. This thermal conductivity is considerably low compared to other material system, and it is practically noticeable. Second phase could also be responsible for this decreasing of thermal conductivity. Electronic thermal conductivity can be calculated using the equation, κ_e = LσT, where L is the Lorenz number (2×10^-8 WΩK^-2).
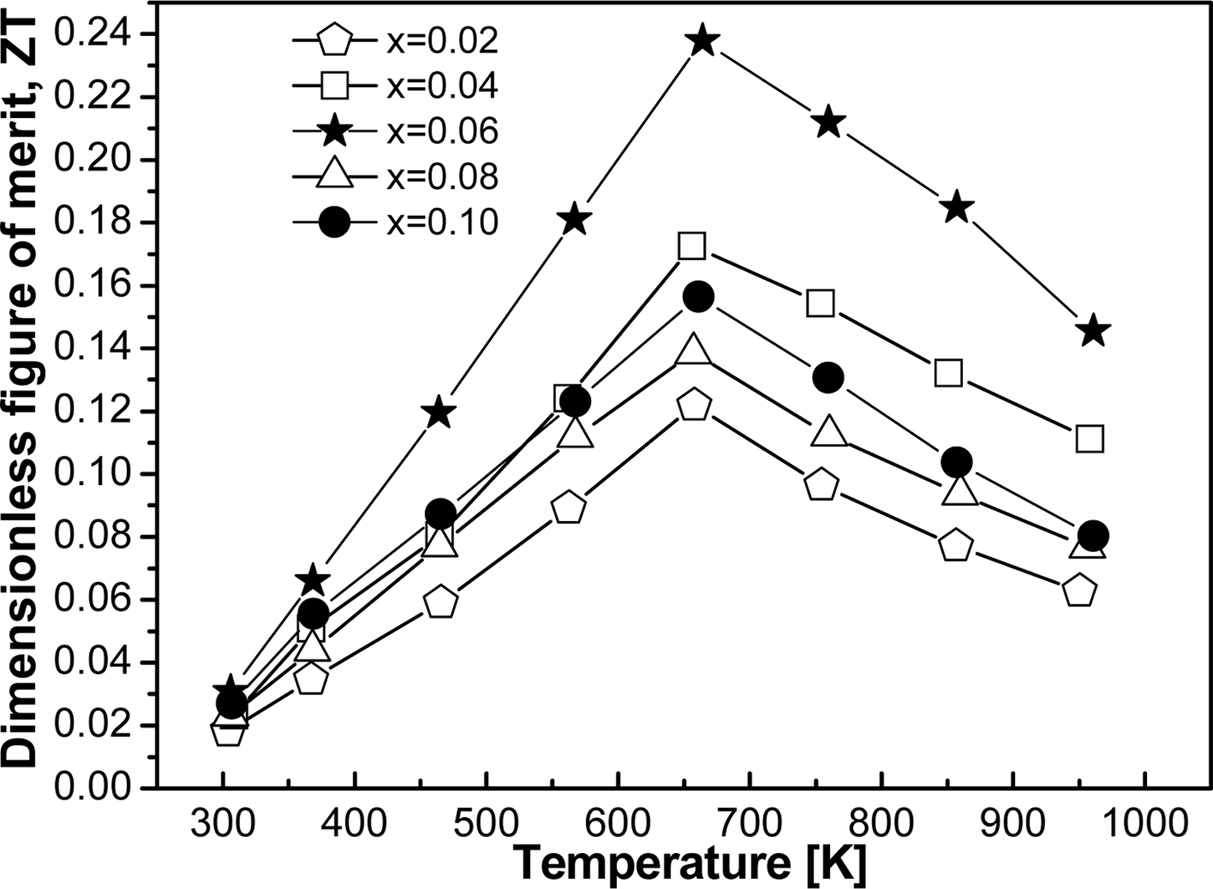
The dimensionless figure of merit (ZT) was calculated from TE properties and shown in Fig. 9 as a function of temperature. The maximum value of ZT is achieved for the sample x = 0.06 at 657 K. This moderate value of ZT could not be enough to be used in a practical TE device. Generally, denser material produced maximum ZT which is evident in this experiment for FeVSb_0.94Te_0.06. The resultant maximum ZT of 0.24 was found due to the impurities free material formation and relatively low thermal conductivity with relatively high Seebeck coefficient. This suggests that careful tuning of the appropriate dopant might produce higher ZT than current experiment. Another way that might be fruitful to improve ZT is multi-doping which could decrease the thermal conductivity to a large fraction and enhance ZT significantly [28].

FeVSb_1-xTe_x (0.02 ≤ x ≤ 0.10) HH alloys synthesized by MA process and subsequent VHP were studied in the temperature range of around 300 to 973 K. It was found that with the increase of Te concentration, the lattice thermal conductivity decreased considerably. The lowest value of lattice thermal conductivity is found to be 2.22 Wm^-1K^-1 at 773 K, which is relatively low for HH compounds. The lowest thermal conductivity was obtained for the composition FeVSb_0.94Te_0.06. This considerable reduction of the lattice thermal conductivity of the FeVSb_0.94Te_0.06 HH alloys might be due to the enhanced phonon scattering, increased effective mass of carriers and second phase interaction by Te substitution at the Sb site in FeVSb matrix. The Seebeck coefficient and electrical conductivity were found to be very sensitive to the Te concentration throughout the process. Te substitution at the Sb site enhanced the ZT of FeVSb_1-xTe_xHH alloys and the maximum ZT was found to be 0.24 at 657 K for FeVSb_0.94Te_0.06. Although the observed highest ZT value is relatively moderate to apply in a TE device, further improvement maybe possible through enhancement of the electrical conductivity and Seebeck coefficient via optimization of appropriate doping at the Fe/V sites and formation of pure single phase.

This work was supported by the Regional Innovation Center (RIC) Program, which was conducted by the Ministry of SMEs and Startups of the Korean Government, and the Korea Basic Science Institute grant funded by the Ministry of Education (grant no. 2019R1A6C1010047).