- Evaluation of thermoelectric and transport properties in Fe1-xMnxVSb half-heusler system synthesized by mechanical alloying process
Rahidul Hasan and Soon-Chul Ur*
Department of Materials Science and Engineering/ReSEM, Korea National University of Transportation, 50 Daehak-ro, Chungju, Chungbuk 27469, Republic of Korea
Mechanical alloying followed by subsequent vacuum hot pressing was utilized for the synthesis of Fe1-xMnxVSb (0.01 £ x £ 0.05) half-Heusler alloys. Controlling doping concentration could make a major effect on thermoelectric properties of this system. Near single half-Heusler phases were found to be dominating in all the samples, however, a fraction of second phases also traced. Investigation of microstructure revealed that ultrafine microstructure was formed in vacuum hot pressed samples. Thermoelectric properties were studied as a function of doping concentration and temperature. The absolute value of Seebeck coefficient was found to be increased with increasing temperature and doping concentration. Electrical conductivity was found to be decreased slightly with increasing temperature. Thermal conductivity and lattice thermal conductivity decreased considerably with increasing temperature, which could be due to increasing effective mass, grain boundary scattering, second phase interaction, and substitutional defect. The resultant maximum thermoelectric figure of merit was found to be 0.21 for x = 0.03 at 567 K. No incorporation of foreign elements was found during handling and processing.
Keywords: Doping, Seebeck Coefficient, Thermal Conductivity, Half-Heusler

|
Fig. 1 Calculated average particle size of as-MAed powders for 8 h; (a) x=0.01, (b) x=0. 02, (c) x=0.03, (d) x=0.04, and (e) x=0.05. |
|
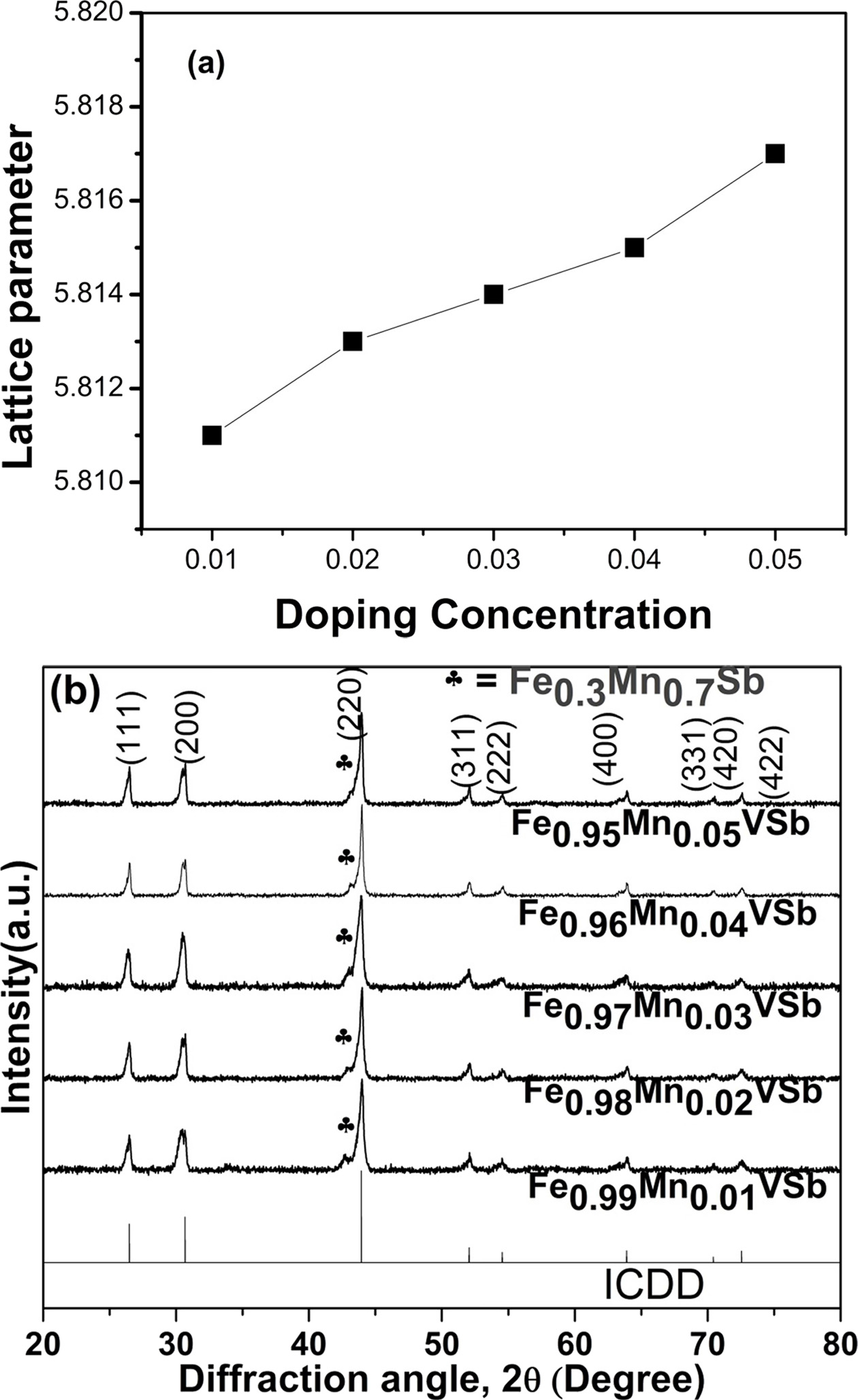
Fig. 2 Change in crystal structure of VHPed samples; (a) lattice parameter as a function of doping concentration, and (b) peak shifting for Fe1-xMnxVSb (x=0.01~0.05). |
|
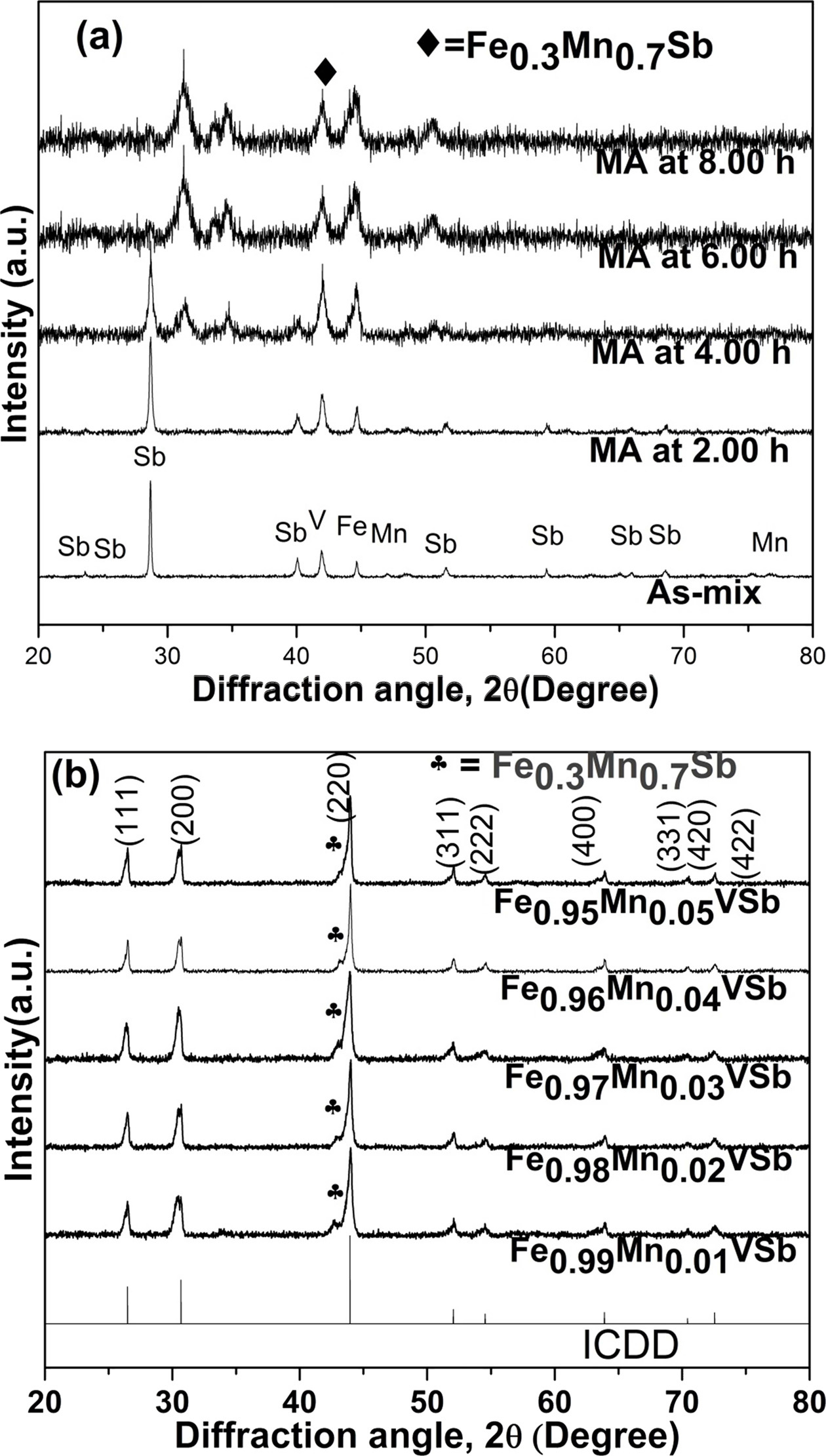
Fig. 3 Phase transition in; (a) MAed powder samples, and (b) near single HH phase with a fraction of secondary phase in VHPed samples. |

|
Fig. 4 SEM images, which showed the microstructure of VHPed Fe1-xMnxVSb; (a) x=0.01, (b) x=0.02, (c) x=0.03, (d) x=0.04, and (e) x=0.05. |
|
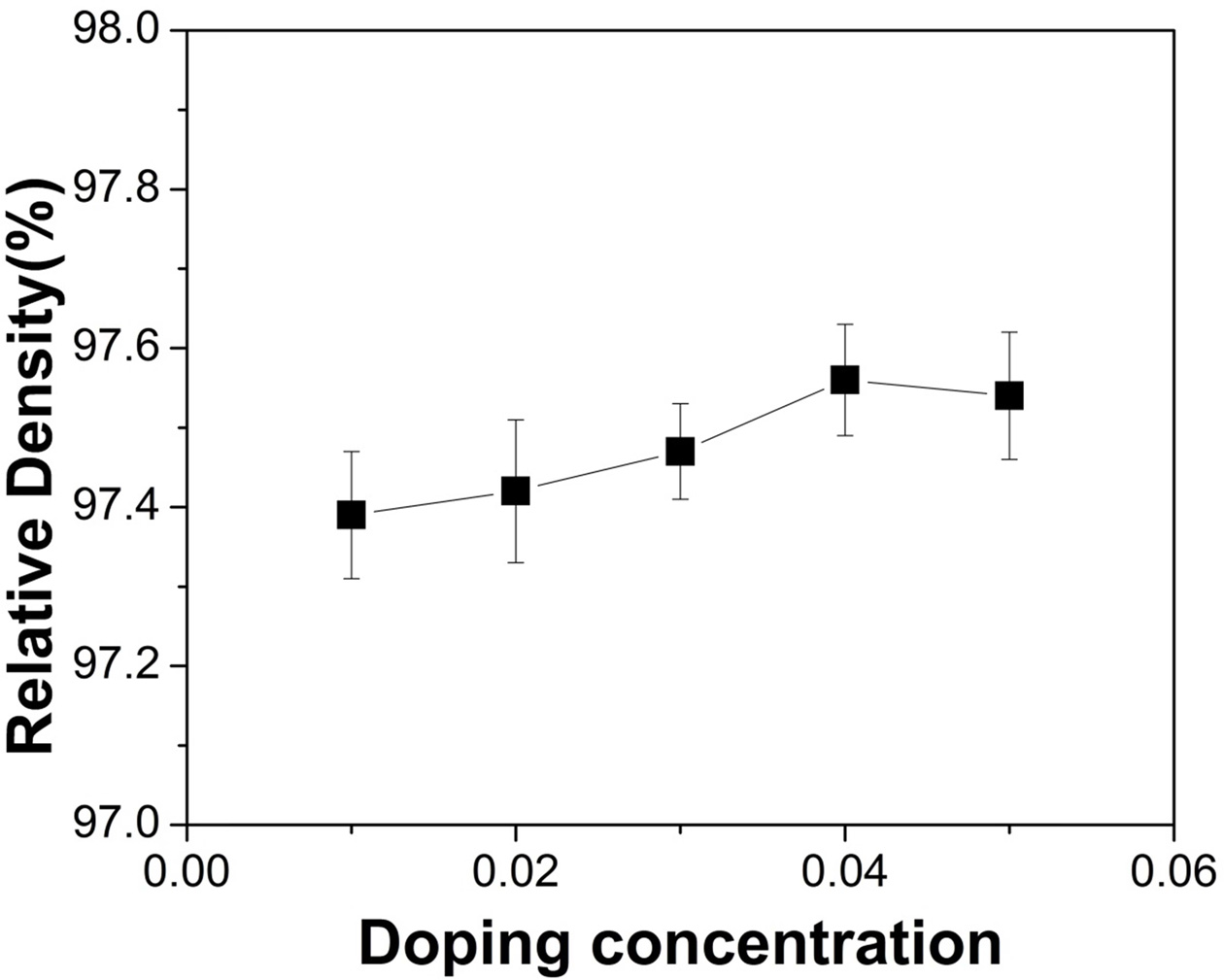
Fig. 5 Calculated relative density, as a function of doping concentration. |
|
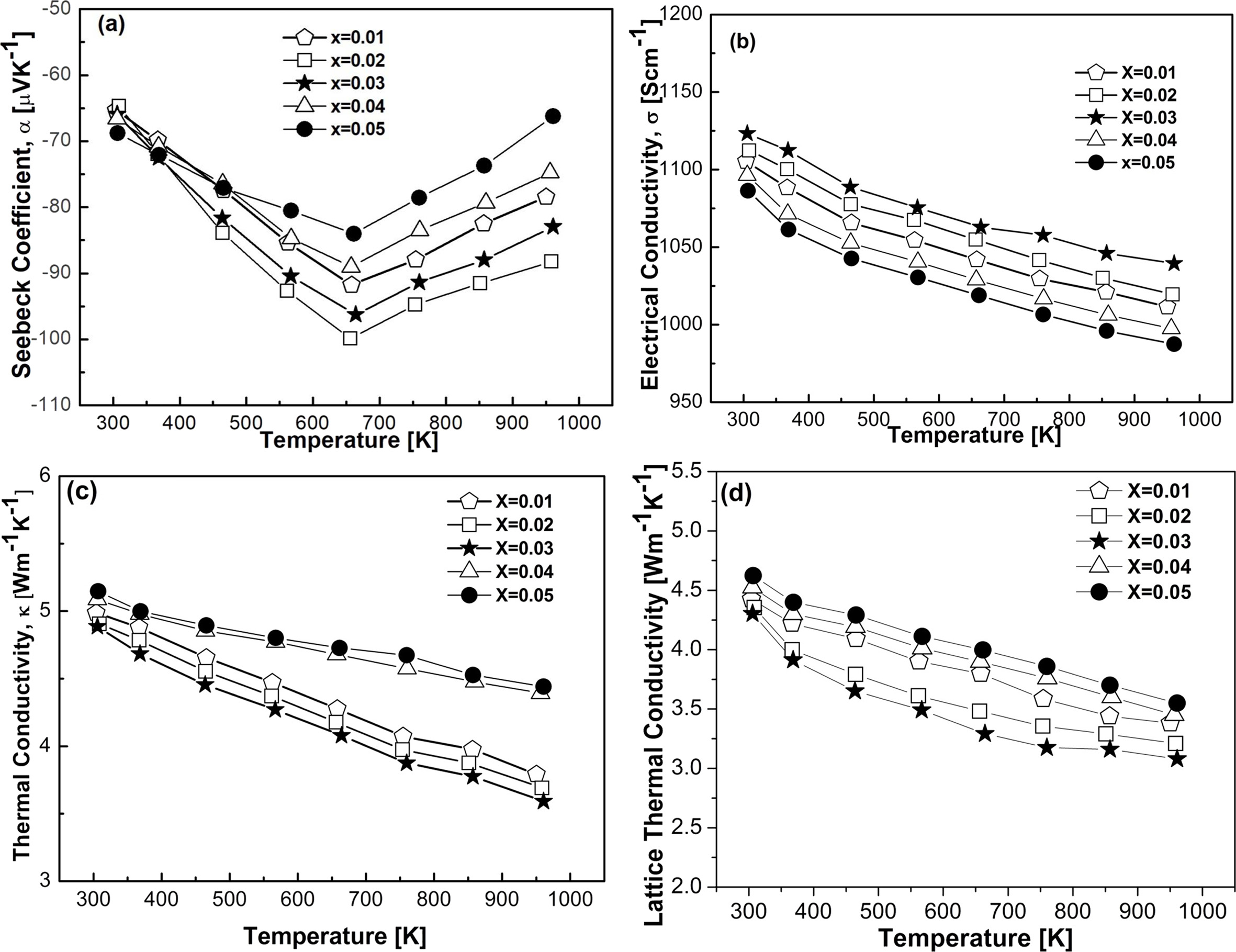
Fig. 6 Thermoelectric properties as a function of temperature and doping elements; (a) Seebeck coefficient, (b) electrical conductivity, (c) thermal conductivity, and (d) lattice thermal conductivity. |
|
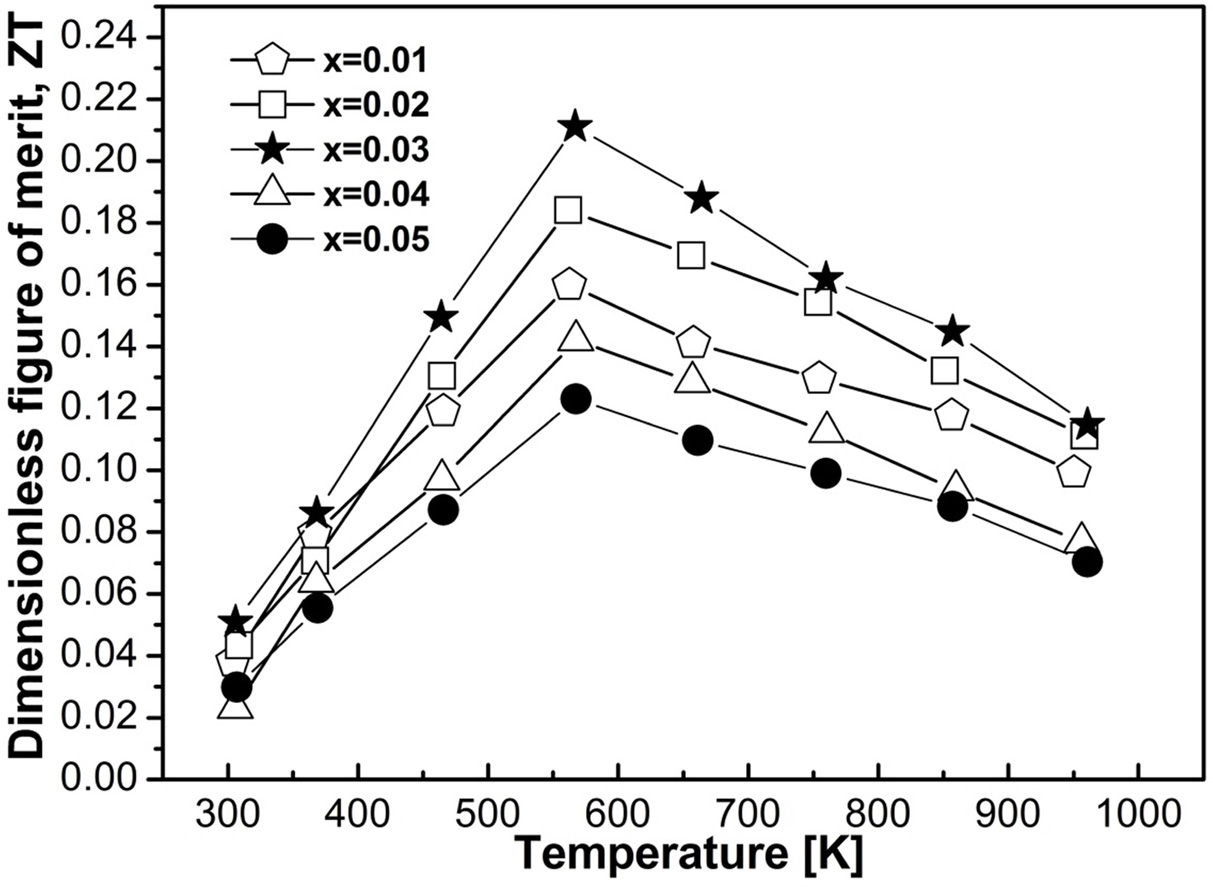
Fig. 7 Calculated ZT as a function of doping elements and temperature. |
|
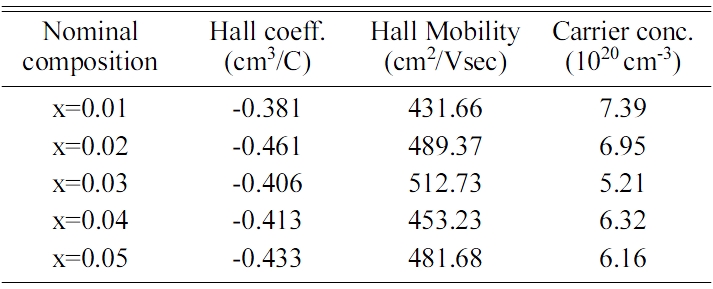
Table 2 Hall measured data for VHPed Fe1-xMnxVSb HH alloys at room temperature. |
This work was supported by the Regional Innovation Center (RIC) Program, which was conducted by the Ministry of SMEs and Startups of the Korean Government.
- 1. J. B. Neaton, Nat. Nanotechnol. 9 (2014), 876.
-

- 2. G. J. Snyder, E. S. Toberer, Nat. Mater. 7 (2008), 105.
-

- 3. Y. Z. Pei, X. Y. Shi, A. Lalonde, H. Wang, L. D. Chen, G. J. Snyder, Nature. 473 (2011), 66.
-

- 4. H. Hohl, A. P. Ramirez, C. Goldmann, G. Ernst, B. Wolfng, E. Bucher, J. Phys. Condens. Matter 11 (1999), 1697.
-

- 5. Y. Xia, V. Ponnambalam, S. Bhattacharya, A. L. Pope, S. J. Poon, T. M. Tritt, J. Phys. Condens. Matter. 13 (2001), 77.
-

- 6. R. Akram, Q. Zhang, D. Yang, Y. Zheng, Y. Yan, X. Su, X. Tang, J. Electron. Mater. 44 (2015), 3563.
-

- 7. D. P. Young, P. Khalifah, R. J. Cava, A. P. Ramirez, J. Appl. Phys. 87 (2000), 317.
-

- 8. M. Zou, J. F. Li, T. Kita, J. of Sol. Stat. Chem. 198 (2013), 125.
-

- 9. C. Uher, J. Yang, S. Hu, D. T. Morelli, G. P. Meisner, Transport Properties of Pure and Doped MNiSn (M = Zr, Hf), Phys. Rev. B. 59 (1999), 8615.
-

- 10. Y. Xia, S. Bhattacharya, V. Ponnambalam, A. L. Pope, S. J. Poon, T. M. Tritt, J. Appl. Phys. 88 (2000), 1952.
-

- 11. S. Sakurada, N. Shutoh, Appl. Phys. Lett. 86 (2005), 082105 (1-3).
-

- 12. S. Populoh, M. Aguirre, O. Brunko, K. Galazka, Y. Lu, A. Weidenkaff, Materials, 6 (2013), 1326.
-

- 13. M. Schwall, B. Balke, Phys. Chem. Chem. Phys. 15 (2013), 1868.
-

- 14. X. Yan, W. Liu, H. Wang, S. Chen, J. Shiomi, K. Esfarjani, H. Wang, D. Wang, G. Chen, Z. Ren, Energy Environ. Sci., 5 (2012), 7543.
-

- 15. E. Rausch, B. Balke, S. Ouardi, C. Felser, Phys. Chem. Chem. Phys. 16 (2014), 25258.
-

- 16. R. Stern, B. Dongre, G. K. H. Madsen, Nanotechnology, 27 (2016), 334002 (1-6).
-

- 17. S. –C. Ur, H. Choo, D. B. Lee, P. Nash, Met. and Mate. Int. 6 (2000), 435.
-

- 18. S. –H. Chang, C. -L. Li, K. -T. Huang, Materials Transactions. 58 (2017), 1190.
-

- 19. A. R. Denton, N. W. Ashcroft, Vegard’s Law, Phys. Rev. A. 43 (1991), 3161.
-

- 20. J. Tobola, L. Jodin, P. Pecheur, H. Scherrer, G. Venturini, B. Malaman, S. Kaprzyk, Phys. Rev. B. 64 (2001), 155103.
-

- 21. C. M. Bhandari, CRC Handbook of Thermoelectrics (Boca Raton: CRC Press, 1995) p.68.
- 22. J. P. Heremans, C. M. Thrush, D. T. Morelli, Phys. Rev. B. 70 (2004), 115334.
-

- 23. J. Cui, G. Cai, W. RenRSC Adv. 8 (2018), 21637.
-

- 24. Adrian P. Mouritz, Introduction to Aerospace Materials (Chapter-4:Strengthening of metal alloys), Woodhead Publishing Limited (Sawston, England), 2012.
- 25. T. T. Khan, I. Mahmud, S. –C. Ur, Kor. J. of Mat. Res. 27 (2017), 416.
-

- 26. R. F. Decker, Metallurgical Transactions. 4 (1973), 2495.
-

- 27. P. Jozwik, Z. Bojar, J. of Metallurgy and Materials. 52 (2007), 321.
 This Article
This Article
-
2019; 20(4): 321-326
Published on Aug 31, 2019
- Received on Dec 28, 2018
- Revised on May 20, 2019
- Accepted on Jul 10, 2019
 Services
Services
- Abstract
introduction
experiments
results and discussion
conclusion
- Acknowledgements
- References
- Full Text PDF
Shared
 Correspondence to
Correspondence to
- Soon-Chul Ur
-
Department of Materials Science and Engineering/ReSEM, Korea National University of Transportation, 50 Daehak-ro, Chungju, Chungbuk 27469, Republic of Korea
Tel : +82-43-841-5385
Fax: +82-43-841-5380 - E-mail: scur@ut.ac.kr






 Copyright 2019 International Orgranization for Ceramic Processing. All rights reserved.
Copyright 2019 International Orgranization for Ceramic Processing. All rights reserved.